一、前言
我发现很多人学了很久的统计学,仍然搞不清楚什么是点估计、区间估计,总是概念混淆,那今天我们来盘一盘统计推断基础的点估计、区间估计。这个系列统计推断基础5部分分别是:
- 总体、样本、标准差、标准误
【定量分析、量化金融与统计学】统计推断基础(1)---总体、样本、标准差、标准误 - 样本均值分布、中心极限定理、正态分布
【定量分析、量化金融与统计学】统计推断基础(2)---样本均值分布、中心极限定理、正态分布 - 点估计、区间估计
- 假设检验
- I型误差,II型误差
重点在基础概念,基础不牢,地动山摇,不关你是做研究还是本科基础学习阶段,基础都是很重要的。
二、点估计
1.定义:
点估计是参数的单值估计。
点估计是用样本数据计算的样本统计量,来估计相应的未知总体参数的最可能值。换句话说,点估计是一个从样本中导出的单值,用于估计总体值。
最常见的例子就是:样本的均值是总体均值的估计值,这就是一个单值估计。
再一个例子:
62是从150名学生中随机抽取15名学生的平均成绩(x),被认为是整个班级的平均成绩。因为它是单数值形式,所以它是一个点估计量。
2.点估计的优点与缺点:
优点:
简便、易行,原理也很直观
但是我们都知道简单的东西肯定会有不完美的地方,因为世界是复杂的。
缺点:
点估计的基本缺点是没有关于可靠性的信息可用。事实上,单个样本统计量等于总体参数的概率非常小。不考虑误差问题。
3.点估计的常见方法(不详细讲):
矩估计法和最大似然估计法。
这里不展开讲,以后会有机会再说的。
三、区间估计(重点说)
1.什么是区间估计
区间估计是抽样推断中根据抽样指标和抽样误差去估计全体指标的可能范围的一种推断方法。
2.置信区间
既然你考虑抽样误差,那么你就得让我知道有多大可能这个估计是可信的,那么就会出现置信区间的概念。
那么置信区间是什么呢?
置信区间表示与特定抽样方法相关的精度和模糊度。另外,置信区间方程由3部分组成:
- 点估计值
- 置信水平
- 误差限界

- 点估计是一个统计值(来自样本的值)是一个参数(来自总体的值)的估计。
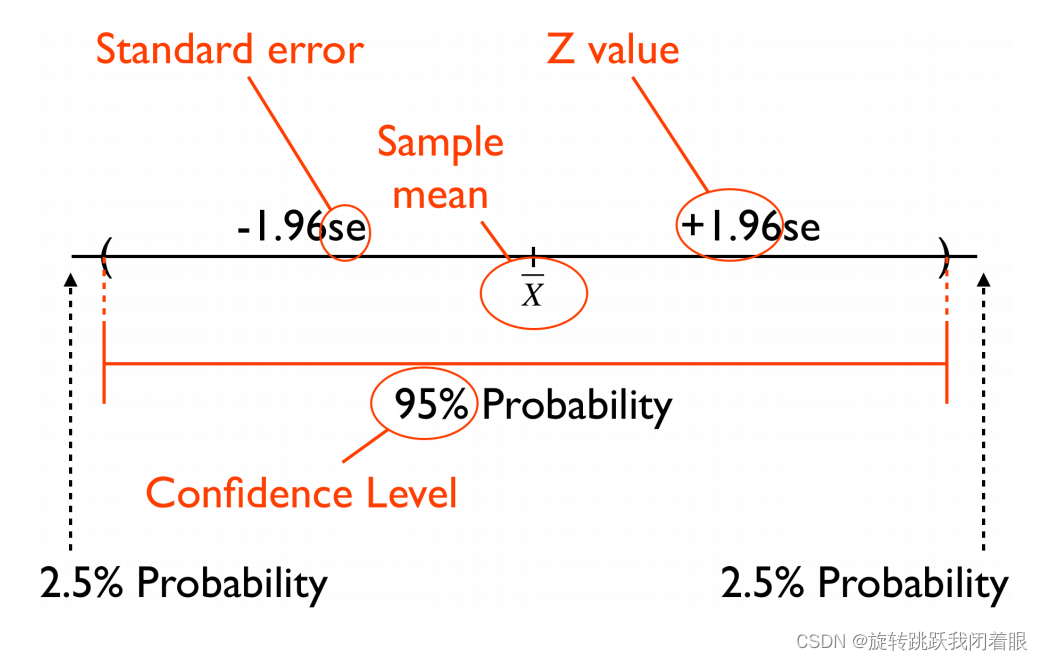
- 置信水平是在任何给定的样本中,该置信区间将包含总体均值的确定性百分比。
- 误差边际是实际总体参数和参数的样本估计之间的最大期望差异。换句话说,它是样本统计量上下的值范围。
3.大样本(大于30的样本容量)区间估计的图示、步骤与例子:
例子:假设我们有一个50个铅笔的样本(大样本,小于30为小样本),一直样本内每一个铅笔的长度。x1,x2,x3...x50,我们来估计总体。
(1)计算样本平均值(x bar)和标准差(SD):
X bar = 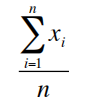
SD = 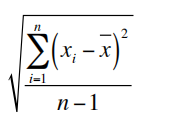
假设我们最后得到:平均值为14.99cm,标准差为0.138
(2)确定置信水平
常见的置信水平:
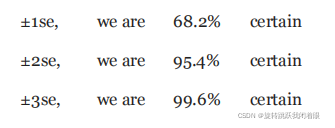

我们一般选95%的置信水平,这是习惯。
另外,你注意,我们目前并不知道标准误(SE),只知道标准差(SD)
所以第三步我们求SE
(3)求标准误(SE)
SE = 
S就是SD,n=50(样本容量)
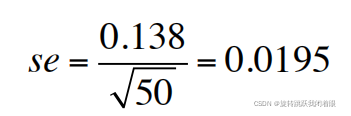
(4)计算置信区间:
目前我们知道的:

我们计算区间估计:

我们的结论是:总体的均值在14.952-15.028之间的可能性为95%
4.小样本(小于30的样本容量)的区间估计
唯一的区别是,不是假设一个正态分布,而是使用T分布。总之,T分布是一个更保守的分布,在相同的置信水平下,置信区间更宽。
所以我们的Z值要换成T值

t的确定需要自由度的概念。那么什么是自由度df呢?
自由度(degree of freedom, df)指的是计算某一统计量时,取值不受限制的变量个数。通常df=n-k。其中n为样本数量,k为被限制的条件数或变量个数,或计算某一统计量时用到其它独立统计量的个数。
那么在区间估计中,我们一般是:
df = n-1
我们就以5的样本容量为例:
假设我这个样本中有5个铅笔,求95%可信度情况下的区间估计:
那么
df = 4
查找t表:
95%置信度,那么就有(1-95%)/2 = 2.5%的单侧错误率

查表得:t值为2.776
带入计算就行,步骤都一样。
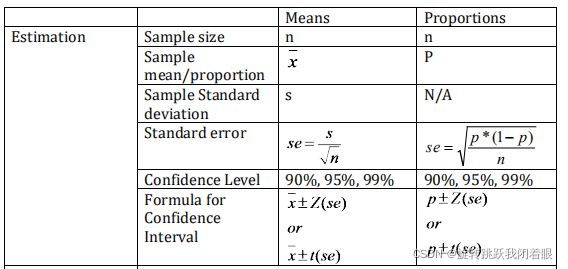
表格与步骤: