参考与这个链接的博客https://blog.csdn.net/paulfeng20171114/article/details/82454310
多目标优化—帕累托(Pareto)
1 多目标优化简介
2多目标优化数学语言描述
3 多目标优化的Pareto占优
1 多目标优化简介:
在现实生活中有很多的问题都是由互相冲突和影响的多个目标组成,这些目标不可能同时达到最优的状态,我们通常会尽量让这些目标在一定的区域内达到最佳的状态,这就是多目标优化。
2 多目标优化数学语言描述:
多目标优化问题是由多个目标函数以及不等式约束条件组成,从数学角度可以做如下描述: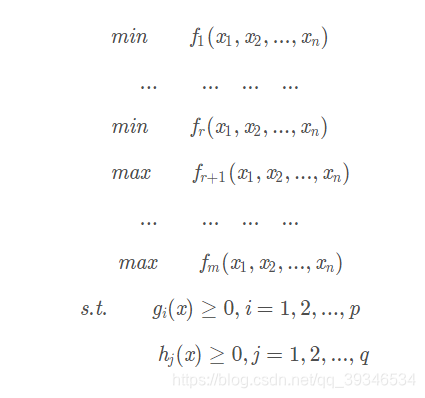
其中fi(x),{i=1,2,…m}是目标函数, gi(x)和hj(x)是约束函数

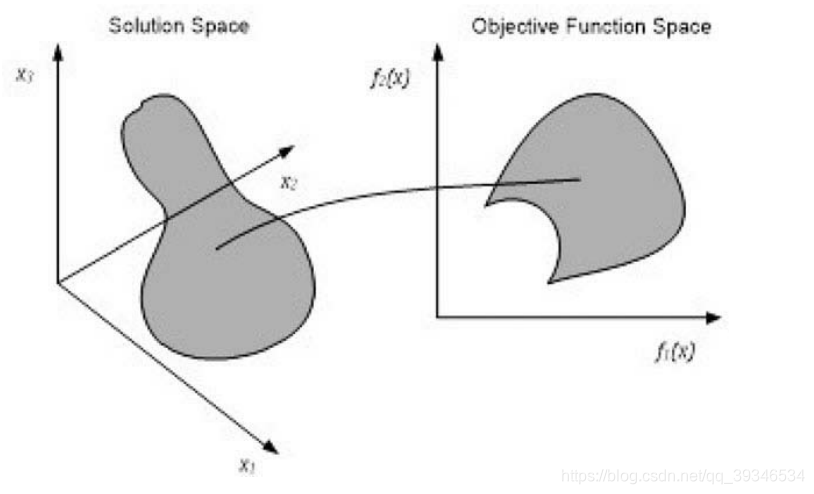
3 多目标优化的Pareto占优
定义1:帕累托占优(Pareto Dominate)

也可称为a支配b,如果对于一个决策变量,不存在其他决策变量能够支配他,那么就称该决策变量为非支配解。
定义2:帕累托最优解
如果在整个参数空间内不存在任何一个决策向量帕累托占优某一个决策向量,就称该决策向量是帕累托最优解。所有帕累托最优解组成的集合称为帕累托最优解集合
定义3:绝对最优解、非劣解、帕累托前沿
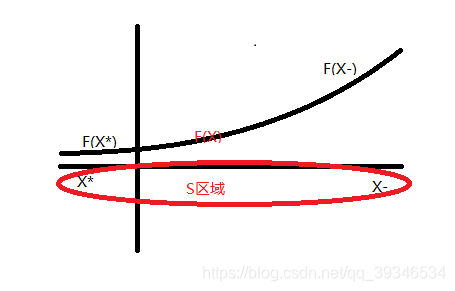
?在决策变量的集合S中,有一个变量X*,对于任意的X属于S,存在目标函数F(X*)<=F(X),则称X*为目标函数的 绝对最优解
?在决策变量的集合S中,有一个变量X-,对于任意的X属于S,存在目标函数F(X)<=F(?,则称X-为目标函数的 最优解(非劣解)
?
?多目标优化问题的非劣解一般不止一个,由所有非劣解构成的集合称为 非劣解集
?所有非劣解对应的目标函数构成了非劣最优目标域也就是帕累托前言