(2)stata的基本使用--分类回归 logit

分类回归

查看系统自带的数据集

导入数据并浏览信息

以上是我记着玩的，均与本节无关。

导入外部数据

数据集下载地址：

	http://econometrics-stata.com/col.jsp?id=101

路径自行解压修改

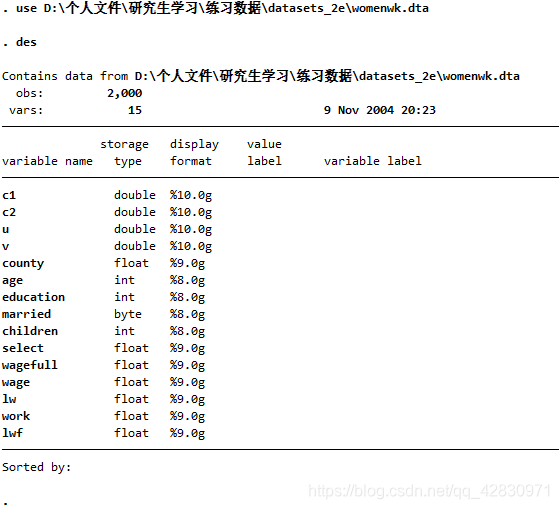
分类二值回归

.线性OLS

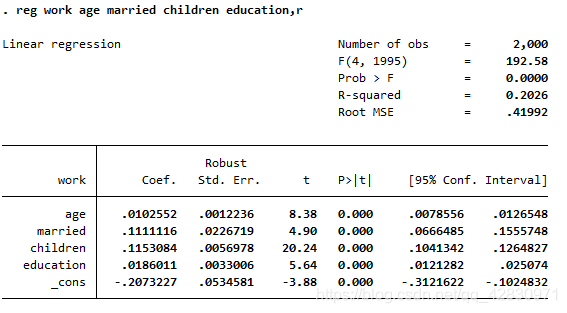
.使用logit回归

估计 $\beta$
函数形式：
P为y=1发生的概率,即每一类的概率

回归命令：

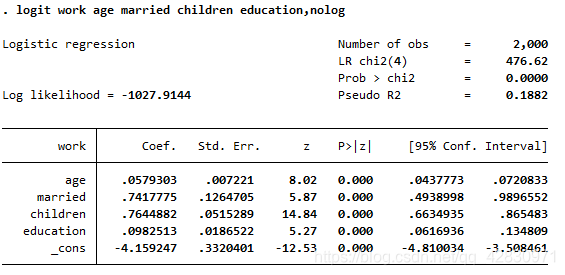
新概念Pseudo R2 表示准R方，

可以写为：

意味着：
（对数函数实际实际取值-只含常数项的对数取值）与（对数自然函数可能的最大取值-只含常数项的对数取值）之比，意味着加入分类变量能够让模型的准确的上升多少。

回归结果的的解读：

LR为476.62，LR的P值检验是0.00000<0.05，说明方程整体是显著的，LR = n*R方 大样本下服从卡方分布

Pseudo R2 表示准R方：有0.1882,其含义类似于拟合优度

其coef为各自变量的系数$\beta$，对应P值为各自显著性水平

	 $exp(\beta)$表示X每增加一单位,导致结果发生的概率比增加的倍数

汇报 $exp(\beta )$的命令如下：

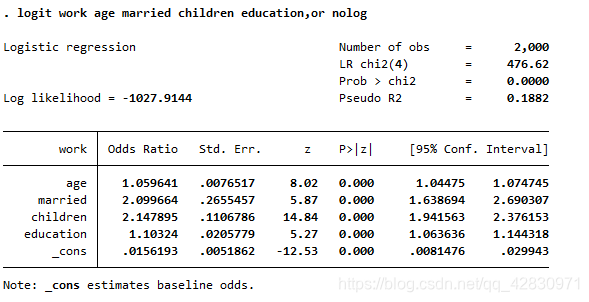
解释：

  以list the example of coefficient about married's and age's 已婚妇女参加工作的几率比是未婚妇女的2.099664倍（即高出109.9664%）；年龄每增加一岁，参加工资的几率比增	加5.9641%，其他的变量类似解释

are you 还 ok?哈哈，继续，如果你不相信这个模型，你可以使用logit稳健标准误差，向下看。

使用logit稳健标准误差进行估计：

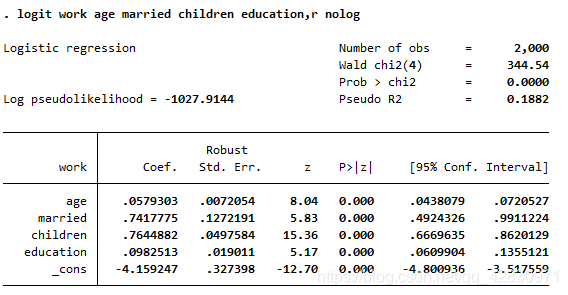
与普通的估计无太大差别，因此不需要担心模型设定偏误
看一下边际效应

细致的分析，边际效应

模型的平均边际效应

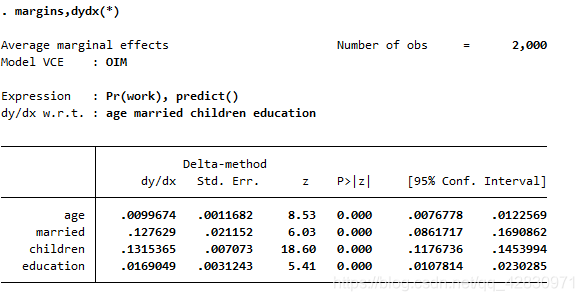
这个结果和使用OLS回归出来的类似，真的类似。都是边际量嘛。

样本均值处的边际效应

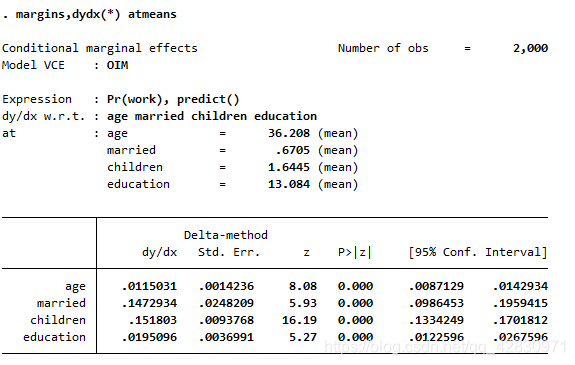
样本特定值的边际效应

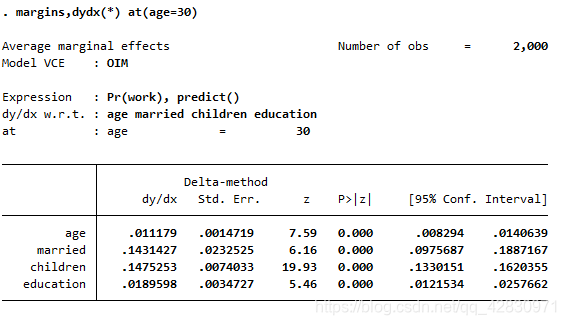
计算Logit的准确预测比率

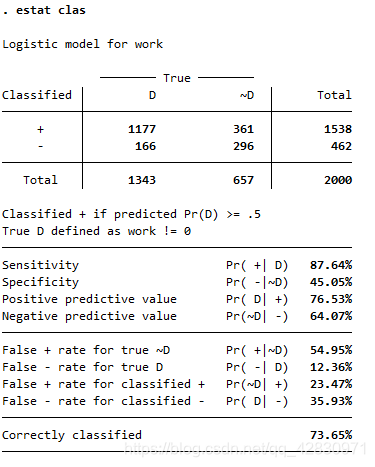
准确率有73.65%，准确率还可以

解决组内相关，聚类变量回归

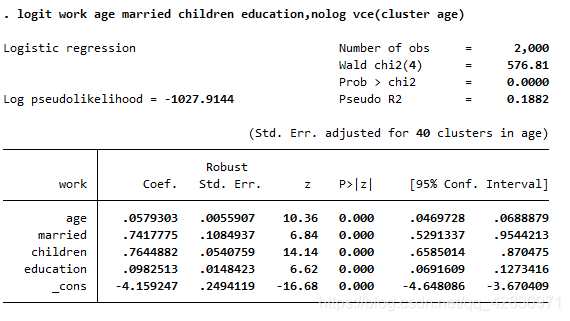
当然了，我们假设了年龄存在组内相关

Probit与Logit是一样的步骤