RL策略梯度方法之(六): Deterministic policy gradient(DPG)

本专栏按照 https://lilianweng.github.io/lil-log/2018/04/08/policy-gradient-algorithms.html 顺序进行总结 。

$DPG$ ：[ paper | code ]

原理解析

Stochastic Policy Gradient (SPG) 是通过参数化的概率分布 ${\pi }_{\theta }(a|s)=P[a|s;\theta ]$ 随机地选择动作，即 ${\pi }_{\theta }(a|s)$ 是一个动作的概率分布。
Deterministic Policy Gradient (DPG) 与SPG 不同之处是，这个方法会确定地选择一个动作： $a={\mu }_{\theta }(s)$ 。

简而言之：

• 随机策略，在同一个状态处，采用的动作是基于一个概率分布的，即是不确定的。
• 确定性策略，虽然在同一个状态处，采用的动作概率不同，只取最大概率的动作。

看起来很奇怪吧！当仅仅只输出一个动作的时候，怎么计算动作概率的梯度呢？
接下来我们一步一步地看看~

回顾策略梯度

1. 策略梯度：
   首先解决一个强化学习问题，我们想到的就是累计折扣奖励的定义，即状态满足 ${\rho }^{\pi }$ 分布上的累计奖励，如下：
   $\begin{array}{rl}J({\pi }_{\theta })=& {\int }_S{\rho }^{\pi }(s){\int }_A{\pi }_{\theta }(s,a)r(s,a)dads\\ =& E_{s?{\rho }^{\pi },a?{\pi }_{\theta }}[r(s,a)]\end{array}$
   ${\rho }^{\pi }(s^{\prime })={\int }_S{\sum }_{t=1}^{\infty }{\gamma }^{t?1}{p}_1(s)p(s\to s^{\prime },t,\pi )ds$

   • $p_1(s)$ 表示初始状态为 $s$ 的概率
   • $p(s\to s^{\prime },t,\pi )$ 表示在策略 $\pi$ 下状态 $s$ 经过t时间步到达 $s\prime$

2. 策略梯度定理：
   那么什么是策略梯度呢？策略梯度就是沿着使目标函数变大的方向调整策略的参数，它被定义为：
   $\begin{array}{rl}{?}_{\theta }J({\pi }_{\theta })=& {\int }_S{\rho }^{\pi }(s){\int }_A{?}_{\theta }{\pi }_{\theta }(s,a)Q^{\pi }(s,a)dads\\ =& E_{s?{\rho }^{\pi },a?{\pi }_{\theta }}[{?}_{\theta }log{\pi }_{\theta }(s,a)Q^{\pi }(s,a)]\end{array}$

3. stochastic Actor-Critic algorithm
   critic 通过TD的方式估计　action-value function：$Q^w(s,a)=Q^{\pi }(s,a)$
   所以，策略梯度定理演化为：$\begin{array}{rl}{?}_{\theta }J({\pi }_{\theta })=& {\int }_S{\rho }^{\pi }(s){\int }_A{?}_{\theta }{\pi }_{\theta }(s,a)Q^w(s,a)dads\\ =& E_{s?{\rho }^{\pi },a?{\pi }_{\theta }}[{?}_{\theta }log{\pi }_{\theta }(s,a)Q^w(s,a)]\end{array}$
   公式非常直白的告诉我们，$J()$ 函数主要与策略梯度和值函数的期望有关，尽管状态空间分布 ${\rho }^{\pi }$ 的分布依赖于策略参数，但是策略梯度并不依赖于状态分布上的梯度。另外， 在DQN中我们使用了 评价网络 和 target网络，采用了experimence replay的方式打乱了数据之间的相关性而使得满足独立同分布条件，利用softupdating方式更新target网络，但总结一句话，它的策略网路和值函数网络使用的是同一个网络。在DPG的公式表明，$J()$ 和策略梯度与值函数有关，因此为了解决策略和值函数之间的问题，采用了一种新的解决思路将两个网络分开，即：Actor-critic异步框架。(Actor就是策略网络，来做动作选择(空间探索)。Critic就是值函数，对策略函数进行评估)，具体的流程如图：
   
   简单描述一下图：其中的TD-error就是Critic告诉Actor的偏差。
   具体的更新过程：

$\begin{array}{rlr}{\delta }_t& =R_t+\gamma Q_w(s_{t+1},a_{t+1})?Q_w(s_t,a_t)& \text{; TD error in SARSA}\\ w_{t+1}& =w_t+{\alpha }_w{\delta }_t{?}_w{Q}_w(s_t,a_t)& \\ {\theta }_{t+1}& ={\theta }_t+{\alpha }_{\theta }{?}_a{Q}_w(s_t,a_t){?}_{\theta }{\mu }_{\theta }(s){|}_{a={\mu }_{\theta }(s)}& \text{; 确定性策略梯度定理}\end{array}$

但是，由于策略的确定性，除非环境中有足够的噪声，否则很难保证足够的探索。我们可以在策略中添加噪声(讽刺的是这会使它变得不确定)或者通过遵循不同的随机行为策略来收集样本来 离线策略地学习它。下面来简单提一下。

4. Off-policy AC
   比如说，在离线策略方法中，训练轨迹是由随机策略 $\beta (a|s)$ 产生的，因此，状态分布遵循相应的折扣状态密度 ${\rho }^{\beta }$。
   行为策略：$\beta (a|s)?={\pi }_{\theta }(a|s)$
   $\begin{array}{rl}{J}_{\beta }({\pi }_{\theta })=& {\int }_S{\rho }^{\beta }(s)V^{\pi }(s)ds\\ =& {\int }_S{\int }_A{\rho }^{\beta }{\pi }_{\theta }(s,a)Q^{\pi }(s,a)dads\end{array}$
   $\begin{array}{rl}{?}_{\theta }{J}_{\beta }({\pi }_{\theta })\approx & {\int }_S{\int }_A{\rho }^{\beta }(s){?}_{\theta }{\pi }_{\theta }(s,a)Q^{\pi }(s,a)dads\\ =& E_{s?{\rho }^{\beta },a?\beta }[\frac{{\pi }_{\theta }(a|s)}{{\beta }_{\theta }(a|s)}{?}_{\theta }log{\pi }_{\theta }(s,a)Q^{\pi }(s,a)]\end{array}$
   注意，由于策略是确定性的，所以我们只需要 $Q^{\mu }(s,{\mu }_{\theta }(s))$ 作为给定状态 $s$ 的估计奖励，而不是 ${\sum }_a\pi (a|s)Q^{\pi }(s,a)$。
   在随机策略的 off-policy 方法中，我们经常使用重要性采样 来纠正 行为和目标政策 之间的不匹配，正如我们上面所描述的。然而，由于确定性策略梯度消除了对动作的积分，我们可以避免重要性抽样。

DPG算法

现在考虑如何将策略梯度框架扩展到确定性政策。【确定性策略梯度定理实际上是随机策略梯度定理的一个极限情况，具体证明见论文】

那么极限情况是啥呢？就是当概率策略的方差趋近于0的时候，就是 确定性策略，即

上面这个式子的推导过程可以理解为 ：

DPG算法本身采用的是PG方法，因而直接对轨迹的价值回报进行求导：${?}_{\theta }{v}_{{\mu }_{\theta }}(s)={?}_{\theta }[Q^{\mu }(s,{\mu }_{\theta }(s))]$

链式法则，由于 ${\mu }_{\theta }(s)$ 与确定性策略价值函数 $Q^{\mu }$ 有关,因而 ：${?}_{\theta }{v}_{\mu }(s)={?}_{{\mu }_{\theta }(s)}[Q^{\mu }(s,{\mu }_{\theta }(s))]{?}_{\theta }{\mu }_{\theta }(s)$

• on-policy的确定性策略梯度算法：
  
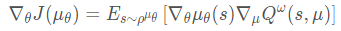
• off-policy的确定性策略梯度算法(Replay buffer中的数据是通过 $\beta$ 采样得到的)，异策略确定性策略梯度：
  
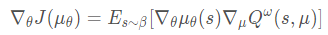
  上两式的区别就是使用了不同的数据采样分布。可以看到off-policy缺少了重要性采样，这是由于确定性策略的动作是固定值，不是一个分布。（$\beta$ 是采样策略， $\mu$ 是评估策略）

该算法采用AC框架：

• [Actor] 衡量一个策略网络的表现(策略网络目标函数)，最大化策略目标: (根据上面推导的DPG)
  $\begin{array}{rl}{J}_{\beta }(\theta )& ={\int }_S{\rho }^{\beta }(s)Q^{\omega }(s,\mu (s))ds\\ & ={\mathbb{E}}_{s?{\rho }^{\beta }}[Q^{\omega }(s,\mu (s))]\end{array}$

  • $s$ 是环境的状态，这些状态 是基于agent 的 行动策略产生的，它们的分布函数 为 ${\rho }^{\beta }$ ；
  • $Q^{\omega }(s,\mu (s))$ 是在每个状态下，如果都按照 $\mu$ 策略选择action时，能够产生的 $Q$ 值。 也即，$J_{\beta }(\mu )$ 是在 $s$ 根据 ${\rho }^{\beta }$ 分布时，$Q^{\omega }(s,\mu (s))$ 的期望值。

• [Critic] 最小化值网络目标:

\qquad${\hat{Q}}^{\omega }(s_t,a_t)=\mathbb{E}[r(s_t,a_t)+\gamma Q^{\omega }(s_{t+1},a_{t+1})]$

\qquad$J_{\beta }(\omega )={\mathbb{E}}_{s?{\rho }^{\beta }}[\frac{1}{2}(r_t+\gamma Q^{\omega }(s_{t+1},a_{t+1})?Q^{\omega }(s_t,a_t){)}^2]$

最终DPG的目标函数为:（ $\omega$ 是值网络 ，$\theta$ 是策略网络 ）

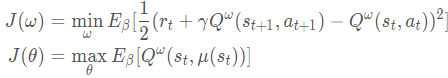
参数更新为：

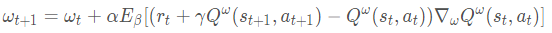
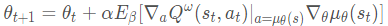
确定性策略梯度的优点在于 需要采样的数据少，算法效率高。

算法实现

总体流程

暂无

代码实现

暂无