LOAM SLAM之论文原理解读

1. 概述

简单整理阅读LOAM论文后对LOAM SLAM的理解，以供自己以后参考。

2. 特点

只需要3d激光点云数据，低漂移，低计算量，
SLAM分为两个部分：10Hz的激光里程计和1Hz的建图
激光里程计使用基于特征点进行相邻点云帧数据匹配，
激光建图使用基于特征点进行校正后输入点云数据和地图拼接。
使用的特征点和对应的特征区域有两类：

1. 使用边缘点以及边缘点所在边缘线，
2. 使用平面点以及平面点所在平面。

在KITTI上里程计排行很高。

3. 术语解释

sweep表示一次完整的数据，一帧点云数据，是多次scan之后得到的点云数据，对应于现在的多线激光雷达，一线代表一个scan，16线激光雷达一次获得的数据就是一次sweep，包含16个scan数据．对于3维点云数据，每次处理的都是一次sweep数据，这样才叫三维，否则不就是二维了吗？仅限于此论文的机械结构，如果使用多线激光，一般一帧数据称为scan。这里是因为二维雷达的原因，术语含义发生了变化，但是本质都是一次完整扫描过程称为scan。
k表示第几次sweep
$P_k$表示第k次sweep的点云数据
L表示激光雷达坐标系，左上前右手坐标系，$X_{k,i}^L$表示$P_k$中点$i$在激光雷达坐标系L下的坐标
W表示三维世界坐标 ，左上前右手坐标系，$X_{k,i}^W$表示$P_k$中点$\text{i}$在世界坐标系W下的坐标
需要解决的问题
给定点云数据序列$P_k$，计算激光雷达在sweep之间的运动并对历史轨迹的周围环境进行建图。

4. 介绍

作者使用单线激光雷达和电机构成了一个多线激光雷达。
激光雷达具体信息：
型号为UTM-30LX 2维激光雷达 25msec/scan,每秒进行40次扫描。
获得的点云数据
水平范围是180°，分辨率为0.25°
使用电机实现垂直扫描，角速度为180°/s。垂直范围为180°，
一次完整的帧数据(sweep)就是水平范围180°，垂直范围180°。耗时1s。

单纯的激光数据会出现畸变，这是为什么呢？

• 激光的点云数据不是同一时间获取的，当sweep开始时激光处于A位置，当sweep结束时激光处于B位置，因为激光扫描时间较长，如果是一堵平行的墙面，理想状况下激光处于A或者B位置测量的距离应该一样，但是实际中激光处于A位置测量的距离和处于B位置的测量的距离一定会出现差异，失去了原始平行墙面的特征，进行激光SLAM时，AB位置的差距必须要考虑，或者说激光在这期间的运动必须要考虑，对应到点云数据会发现，点云数据出现较大的偏移。因此在数据处理时需要构造激光运动模型来消除点云畸变带来的影响。
  
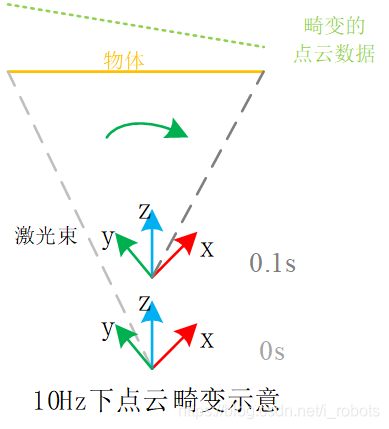
  如下图所示，由于机器人的运动，激光里程计直接获得的数据与实际数据点位置存在差异，因此需要进行修正。原始点云数据经过激光里程计修正之后畸变效果明显降低。
  
  整个LOAM的流程：点云注册，激光里程计（高频低精度），激光建图（低频高精度），坐标发布。
  

5. 特征点提取

特征点包括边缘点和平面点

$S$是第$k$帧点云数据中点$i$对应$X_{ki}^L$附近的一个连续点集合，下式表示的含义：
根据点$i$和$S$中点的归一化矢量和的模来判断点i的类型，如果模大，则为边缘点，模小则为平面点。$|S|$表示$S$中点的数量。

如下图所示，边缘点的矢量和的模一般较大，矢量和不为零向量，而对应平面点的矢量和的模一般较小，矢量和为零向量。

将每次scan扫描得到的点云数据均匀分为四个区域，每个区域最多包含2个边缘点，4个平面点。
需要丢弃不可靠点，例如下面a中的B点，所在平面和激光束平行；下面b中的A点，实际中处于平面特征，由于被遮挡的原因可能被视为边缘点，因此不是真正的边缘点，在相邻帧数据中可能不会再次观测到。这两类点需要进行排除。
还有离群点：某点与左右相邻两个点的距离过大。

因此选择特征点时需要满足条件：

1. 特征点数量满足子区域最大值，每个子区域的特征点数目是一定的，防止过多的特征点。
2. 特征点周围点不能再次被选择，本来每个子区域的特征点数量就比较少了，进一步防止特征点集中分布。
3. 特征点非平行激光束的平面点，非被遮挡的平面点，非离群点。这些都是不可靠的点云数据，不能在连续两帧点云数据中得到，不能作为特征点。

下图就是找到的边缘点（黄色），平面点（红色），由于激光雷达处于运动中，这个时候还存在点云畸变，未进行校正，暂时也不能进行校正。

6. 寻找特征点关系

对于边缘点，寻找边缘点和边缘点所在直线的关系，对于平面点，寻找平面点和平面的关系。
$P_k$开始的时间戳为$t_k$，结束的时间戳为$t_{k+1}$，经过畸变校正之后将$P_k$重投影到$t_{k+1}$得到${\bar{P}}_k$。
估计激光雷达运动时，使用的是
重投影点云数据(经过畸变校正)${\bar{P}}_k$和新的点云数据（未经过畸变校正）$P_{k+1}$。

$E_{k+1}$和$H_{k+1}$分别表示在$P_{k+1}$（未经过畸变校正）中找到的边缘点和平面点集合。对应的，我们需要在${\bar{P}}_k$中找到与$E_{k+1}$中边缘点对应的边缘线和与$H_{k+1}$中平面点对应的平面。

• 这里简单说一下，为什么？理想情况下，没有畸变，激光雷达在短时间里获取的相邻帧数据是含有大量同一特征点的，就是$P_{k+1}$和$P_k$中很多特征点只是雷达在不同位置下观察的同一个点。（前面已经去除了不可靠的特征点），那么现在只要找到一个变换关系$T$使$P_{k+1}$和$P_k$中对应的点重合，那这个$T$实际上表示了激光雷达的帧间运动。为了减少计算量，增加鲁棒性，不直接使用点与点的匹配，而是使用边缘点和对应的线特征，平面点和对应的面特征，这样也可以得到变换关系$T$。然而现在的点云数据是含有畸变的，并且将矫正的$P_k$也重投影到了$t_{k+1}$时刻，那么现在就是一边进行矫正，一边进行匹配。直到所有点和对应特征区域距离和最小。这就是一个迭代的过程，迭代时，变换关系$T$一直在发生变化，$T$的变换使$所有点和对应特征区域距离和$一直朝着最小的方向前进。

每次迭代计算进行时都会将$E_{k+1}$和$H_{k+1}$中的特征点重投影到$k+1$次sweep开始$t_{k+1}$（这是因为我们可以参考的只有 上一帧 矫正后 重投影到$t_{k+1}$的数据${\bar{P}}_k$），使用${\tilde{E}}_{k+1}$和${\tilde{H}}_{k+1}$表示迭代过程中重投影到$k+1$次sweep开始$t_{k+1}$的点集合。对于${\tilde{E}}_{k+1}$和${\tilde{H}}_{k+1}$中的每个点，我们需要在${\bar{P}}_k$中找到最近邻点（这个时候他们的时间戳都是$t_{k+1}$，因此可以进行匹配）。

下图表示了如何寻找边缘点构成边缘线以及如何寻找平面点构成平面。

边缘点与边缘线：在a中，$i$是${\tilde{E}}_{k+1}$中的一个点，$j$是${\bar{P}}_k$中与$i$最近邻点，$l$是$j$相邻两次扫描中与$i$最近邻的点，也就是$j$和$l$不是同一次scan扫描得到的点（一次scan扫描只能包含边缘线中的一个点，否则它就不是边缘线了，相邻两次扫描是为了防止运动畸变过大导致边缘线特征提取不正确，因为构造的问题，使用的激光在不同的scan下同一方位角对应时间戳的差距还是挺大的，近似一个scan周期）。因此$j$和$l$构成了$i$对应的边缘线，并且他们均为${\bar{P}}_k$中的边缘点。
点$i,j,l$分别所在的集合：$i$属于${\tilde{E}}_{k+1}$，$j$和$l$属于${\bar{P}}_k$，并且不同的scan线中。

平面点与平面：在图b中，$i$是${\tilde{H}}_{k+1}$中的一个点，$j$是${\bar{P}}_k$中与$i$最近邻点，为了确定一个平面，至少需要三个不在同一直线上的点。$l$是与$j$同一次scan扫描中与$i$最相邻的点，$m$是$j$相邻两次scan扫描中与$i$最近邻的点，也就是$j$和$m$不是同一次scan扫描得到的点，$j$和$l$是同一次scan扫描的点。$j$、$l$和$m$构成了$i$对应的平面，并且他们均为${\bar{P}}_k$中的平面点。
点$i,j,l,m$分别所在的集合：$i$属于${\tilde{E}}_{k+1}$，$j$、$l$和$m$属于${\bar{P}}_k$，对应的scan前面分析过了。

根据匹配的原理，可以构造优化问题：求解变换关系$T$使边缘点和边缘线距离最短，平面点和平面距离最短
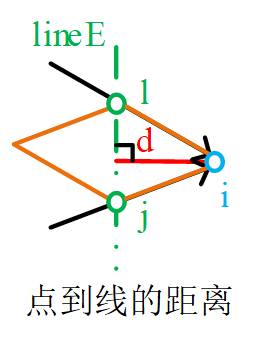
对于点与线的距离计算有：
叉乘表示向量组成的平行四边形面积，面积/边 = 高。这里的高就是距离

公式计算如下
${\tilde{X}}_{k+1,i}^L$表示迭代过程中重投影的第$k+1$帧数据中的点，时间戳由$t_{X_{k+1,i}}$变换到第$k+1$帧数据的开始$t_{k+1}$，使用了匀速运动模型。
${\bar{X}}_{k,j}^L$表示经过校正的第$k$帧数据，经过重投影之后所有点的时间戳均为第$k$帧数据的末尾$t_{k+1}$。

$$d_E=\frac{|({\tilde{X}}_{k+1,i}^L?{\bar{X}}_{k,j}^L)\times ({\bar{X}}_{k+1,i}^L?{\bar{X}}_{k,l}^L)|}{({\bar{X}}_{k,j}^L?{\bar{X}}_{k,l}^L)}$$

可以参考下面的图理解

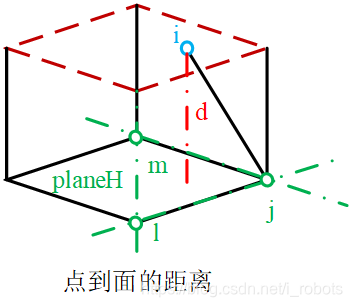
对于点和平面距离有：
叉乘表示向量组成的平行四边形面积，叉乘再点乘表示立体的体积，体积/面积 = 高。这里的高就是距离。
公式如下，说一下每个点所处的时间戳吧，
${\tilde{X}}_{k+1,i}^L$表示迭代过程中重投影的第$k+1$帧数据中的点，时间戳由$t_{X_{k+1,i}}$变换到第$k+1$帧数据的开始$t_{k+1}$，使用了匀速运动模型。
${\bar{X}}_{k,j}^L$表示经过校正的第$k$帧数据，经过重投影之后所有点的时间戳均为第$k$帧数据的末尾$t_{k+1}$。

$$d_H=\frac{|({\tilde{X}}_{k+1,i}^L?{\bar{X}}_{k,j}^L)(({\bar{X}}_{k,j}^L?{\bar{X}}_{k,l}^L)\times ({\bar{X}}_{k,j}^L?{\bar{X}}_{k,m}^L))|}{({\bar{X}}_{k,j}^L?{\bar{X}}_{k,l}^L)\times ({\bar{X}}_{k,j}^L?{\bar{X}}_{k,m}^L)}$$

可以参考下面的图理解

理想下，距离均为0，也就是边缘点位于边缘线，平面点位于平面。但这是不可能的。只能找到一个不为0的最小值。

7. 运动估计

根据特征点可以进行运动估计，这个运动估计是通过相邻两帧激光雷达点云数据估计两帧激光雷达之间的运动，这个运动其实就是我们前面多次提到的变换关系$T$，它描述了相邻两帧点云数据（注意畸变校正与否的问题，时间戳）的变换关系，其实就对应着在获取到相邻两帧点云数据时激光的位姿变换，也就是所谓的运动，经过累积，就可以形成从开始到当前的激光运动，构成激光里程计。
假设激光处于匀速线运动、角运动状态。

下面的表示方法和论文中稍有不同，请注意

$t_k$表示第$k$次sweep的开始时间。
$T_{k,k+1}^L$表示激光点云数据在$[t_k,t_{k+1}]$之间的位姿变换。该位姿变换处于3维空间，拥有6个自由度，包含了平移和旋转。$T_{k,k+1}^L$的定义如下

$$T_{k,k+1}^L=[{\theta }_x,{\theta }_y,{\theta }_z,t_x,t_y,t_z{]}^T$$

给第$i$个点$X_{k,i}$，属于$P_k$，时间戳为$t_a$。对应的位姿变换为$T_{k,a}^L$（这个量和激光的位姿变换是存在一定转换的，不一定直接相等），表示激光点云数据在$[t_k,t_a]$之间的位姿变换。通过线性插值，$T_{k,a}^L$可以由$T_{k,k+1}^L$得到

$$T_{k,a}^L=\frac{t_a?t_k}{t_{k+1}?t_k}{T}_{k,k+1}^L$$

根据假设的匀速运动模型，因此可以得到

时间戳为$t_a$的点$X_{k,i}$ 和 投影到第$k$次sweep开始的点${\tilde{X}}_{k,i}$（时间戳为$t_k$）变换关系。这里和前面的定义能稍稍不一样，但是都一样，只不过为了方便表示，投影到$t_k$时刻。
那么可以得到关系式如下，这里的点$X_{k,i}$均为$P_k$中的特征点，也就是进一步属于$E_k$，$H_k$，对应时刻为$t_a$，而点${\tilde{X}}_{k,i}$为${\tilde{E}}_k$，${\tilde{H}}_k$中的特征点，对应时刻为$t_k$。

$$X_{k,i}^L=R_{k,a}^L{\tilde{X}}_{k,i}+t_{k,a}^L$$

上面的$R_{k,a}^L$和$t_{k,a}^L$可以通过$T_{k,a}^L$得到。分别表示旋转（使用RPY欧拉角构造）和平移（直接对应）。
对应的点云坐标转换表示图如下

• 是不是被上面的公式搞得更加混混混了？可以这样考虑，根据上面这张图，我们现在拥有$t_k$时刻的畸变校正的点云数据${\bar{P}}_{k?1}$以及未校正的点云数据$P_k$，什么叫未校正呢？就是点云数据不是同一个时刻获得的，因此需要进行运动模型校正，使用匀速模型得到的位姿变换$T_{a,k}^L$把$t_a$时刻的点$X_{k,i}^L$统一转换到$t_k$时刻得到${\tilde{P}}_k$，这样拥有同一个时间戳的点云数据${\bar{P}}_{k?1}$和${\tilde{P}}_k$，就可以对点与线距离、点与面距离进行迭代优化得到最优的位姿变换$T_{a,k}^L$。

刚才是不是谈到了$T_{a,k}^L$，这个是干嘛的呢？

根据$$X_{k,i}^L=R_{k,a}^L{\tilde{X}}_{k,i}+t_{k,a}^L$$

可以得到$$R_{a,k}^L(X_{k,i}^L?t_{k,a}^L)={\tilde{X}}_{k,i}$$

上面的$R_{a,k}^L$和$t_{k,a}^L$可以通过$T_{a,k}^L$得到。$T_{a,k}^L$和$T_{k,a}^L$是一组逆运算。平移量可以直接反，但是旋转需要角度和变换顺序同时取反。

因此可以将之前的边缘点和边缘线距离计算，平面点和平面距离计算简化为下面的公式

$$f_E(X_{k,i}^L,T_{k,k+1}^L)=d_E，X_{k,i}^L\in E_{k+1}$$

$$f_H(X_{k,i}^L,T_{k,k+1}^L)=d_H,X_{k,i}^L\in H_{k+1}$$

将所有的特征点和对应的区域距离公式组合，可以得到一个
$$f(T_{k,k+1}^L)=?\begin{array}{c}{f}_E(X_{k,a_1}^L,T_{k,a_1}^L)\\ f_E(X_{k,a_2}^L,T_{k,a_2}^L)\\ ......\\ f_H(X_{k,a_1}^L,T_{k,a_1}^L)\\ f_H(X_{k,a_2}^L,T_{k,a_2}^L)\end{array}?=?\begin{array}{c}{d}_{E,a1}\\ d_{E,a2}\\ ......\\ d_{H,a1}\\ d_{H,a2}\end{array}?=d$$

这是一个非线性优化问题，可以通过GN求解，直到d最小化。

$$J=?f/?T_{k,k+1}^L$$

$$J^{T}J\Delta T_{k,k+1}^L=?J^{T}d$$

8. 激光里程计算法流程

基本上都是我们之前介绍的流程，多说一句，对于第$k$帧数据$P_k$，会使用估计的位姿变换投影到$t_{k+1}$时刻得到${\bar{P}}_k$，供下一次估计帧间运动使用。

9. 建图

累计一定帧数目的点云数据才会进行建图，频率较低，但是精度很高。

目的：将点云数据融入到世界地图中，精确估计激光在世界坐标系的位姿。

与里程计相比，这里构建边缘线，平面时使用的点数大大增加，因此需要采用其他方法得到线向量，法向量。

• 因为里程计使用的点数较少，因此对于线，使用两个点就可以确定这个线向量，但是对于建图部分使用的点数较多，不能直接得到线向量，对于这个问题如何结果，作者使用了协方差矩阵。

根据数学知识，可以得到一个区域的三维点坐标分布与这些点三维坐标形成的协方差矩阵是存在一定关系的。对应的话就是

对于在近似一条线上的点，它们的协方差矩阵中特征值存在两小一大（${\lambda }_1>>{\lambda }_2>{\lambda }_3$），其中${\lambda }_1$对应的特征向量就是这些点所在的线向量。

对于在近似平面的点，它们的协方差矩阵中特征值存在两大一小（${\lambda }_1>{\lambda }_2>>{\lambda }_3$），其中${\lambda }_3$对应的特征向量就是这些点所在平面的法向量。

然后可以建立${\bar{P}}_k$中点和地图中点形成线，${\bar{P}}_k$中点和地图中点形成面的距离关系，使用非线性优化同样可以进一步得到更精确的位姿变换。

${\bar{P}}_k$的点都含有同一个时间戳，已经经过校正，暂时不需要再使用匀速运动模型，但是得到精确化位姿之后会将${\bar{P}}_k$进一步通过$T_k^W$（表示第$k$帧点云数据从局部坐标系$L$到世界坐标系$W$的变换关系）转换到地图中，并且使用体素滤波器对点云数据进行下采样。

位姿的组合如下面所示，蓝色表示建图算法得到的位姿变换$T_k^W$。橘色表示通过里程计算法计算得到粗略的位姿变换$T_{k+1}^L$。

10. 总结

LOAM整体框架如下

点云注册 :构造匀速模型，去除不可靠点，提取点云特征。
里程计 :帧点云配准，计算里程计信息。
建图 :局部点云融合到全局地图，计算精确位姿。
坐标发布 :发布坐标信息，供显示使用。每个节点程序同样也在发布坐标转换！

LOAM的优点：

将里程计和建图分隔开，一个高频低精(处理每次帧数据)，一个低频高精(累积一定次数)
整理框架是串行结构，将整个问题逐步划分为多个层次。
可实时建图的开源3D Lidar SLAM

LOAM的缺点：

点云特征处理可进一步改善：运动的人等物体
回环检测
假设匀速运动模型

11. 参考链接

Zhang J , Singh S . Low-drift and real-time lidar odometry and mapping[J]. Autonomous Robots, 2017, 41(2):401-416.
Zhang J , Singh S . LOAM: Lidar Odometry and Mapping in Real-time[C]// Robotics: Science and Systems Conference. 2014.