【码上实战】【立体匹配系列】经典AD-Census: （3）代价计算_综合

海内存知己，天涯若比邻。

下载完整源码，点击进入: https://github.com/ethan-li-coding/AD-Census
欢迎同学们在Github项目里讨论！

上篇主类中，我们对ADCensusStereo类做了较为详细的介绍，对于具体的算法实现并未过多的设计，本篇即开始带大家了解算法每个具体的功能模块的代码。

首先，是ADCenusu算法的第一个步骤：代价计算！

文章目录

- 算法
- 代码实现
- - 类设计
  - 类实现
- 实验

算法

在原理篇 > 【理论恒叨】【立体匹配系列】经典AD-Census: （1）代价计算中，博主已经对代价计算的原理有过交代，代价由AD代价和Census代价两部分之和组成。总代价公式如下：

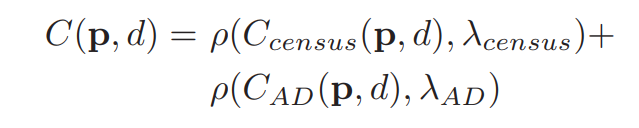
其中，

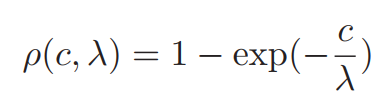
公式是很简单的，AD代价 $C_{AD}$ 为两个像素的颜色三通道差值的均值。

Census代价 $C_{census}$ 的计算方法则在博文SGM:代价计算中讲的很明白，不再赘述。

代码实现

类设计

我将代价计算写成一个类CostComputor，放在文件cost_computor.h/cost_computor.cpp中。

/*** \brief 代价计算器类*/
class CostComputor {
    
public:CostComputor();~CostComputor();
}

当然需要为CostComputor类设计一些公有接口，从而可以调用它们来达到计算代价的目的。

第一个我想到的是 初始化函数Initialize ，为计算代价做一些准备工作，比如我输入的彩色数据，但是计算Census需要灰度数据，所以我需要预分配一个保存灰度数据的数组。

第二个我想到的是 设置数据SetData 以及 设置参数SetParam ，这似乎是必不可少的，巧妇难为无米之炊，没有一个类能够在没有数据和参数的情况下把活干好。

第三个就是计算代价的接口 Compute 了，前面做的一切都是为了能够执行该接口以顺利完成代价计算。

最后一个是获取初始代价的指针 get_cost_ptr ，这意味着我将初始代价数据全权交给CostComputor来管理，我想这样职责会更加清晰。

我们来看看最终的类接口设计：

public:/*** \brief 初始化* \param width 影像宽* \param height 影像高* \param min_disparity 最小视差* \param max_disparity 最大视差* \return true: 初始化成功*/bool Initialize(const sint32& width, const sint32& height, const sint32& min_disparity, const sint32& max_disparity);/*** \brief 设置代价计算器的数据* \param img_left // 左影像数据，三通道* \param img_right // 右影像数据，三通道*/void SetData(const uint8* img_left, const uint8* img_right);/*** \brief 设置代价计算器的参数* \param lambda_ad // lambda_ad* \param lambda_census // lambda_census*/void SetParams(const sint32& lambda_ad, const sint32& lambda_census);/** \brief 计算初始代价 */void Compute();/** \brief 获取初始代价数组指针 */float32* get_cost_ptr();

如上接口全部为公有函数，类的调用端可按逻辑次序调用。（意思就是不能先调用 Compute 再调用 Initialize 哦！）

为了完成代价计算，我们最关键的还是要实现具体的功能函数，我将其放到私有成员函数列表中，分别是计算灰度函数ComputeGray、Census变换函数CensusTransform、计算代价ComputeCost。你或许想问计算AD代价呢？因为其比较简单，所以我直接就在 ComputeCost 中实现了AD代价计算。

private:/** \brief 计算灰度数据 */void ComputeGray();/** \brief Census变换 */void CensusTransform();/** \brief 计算代价 */void ComputeCost();

最后是类所不可或缺的成员变量，比如影像尺寸、影像数据、算法参数、存储灰度数据的数组、存储Census变换值的数组、初始代价数组等，正是它们在类的作用域内始终保持着算法计算所需要的值，才能达到最后的计算目的。得用私有类型把它们保护起来，仅限类的内部使用，我们来看看吧！

private:/** \brief 图像尺寸 */sint32	width_;sint32	height_;/** \brief 影像数据 */const uint8* img_left_;const uint8* img_right_;/** \brief 左影像灰度数据 */vector<uint8> gray_left_;/** \brief 右影像灰度数据 */vector<uint8> gray_right_;/** \brief 左影像census数组 */vector<uint64> census_left_;/** \brief 右影像census数组 */vector<uint64> census_right_;/** \brief 初始匹配代价 */vector<float32> cost_init_;/** \brief lambda_ad*/sint32 lambda_ad_;/** \brief lambda_census*/sint32 lambda_census_;/** \brief 最小视差值 */sint32 min_disparity_;/** \brief 最大视差值 */sint32 max_disparity_;/** \brief 是否成功初始化标志 */bool is_initialized_;

我用vector来存储数据，不再像之前的算法一样使用过多的指针（部分同学会觉得指针比较难用），这样大家更容易接受，我也不用在管内存释放了。

类实现

我们先看看代价计算类CostComputor的初始化函数实现：


bool CostComputor::Initialize(const sint32& width, const sint32& height, const sint32& min_disparity, const sint32& max_disparity)
{
    width_ = width;height_ = height;min_disparity_ = min_disparity;max_disparity_ = max_disparity;const sint32 img_size = width_ * height_;const sint32 disp_range = max_disparity_ - min_disparity_;if (img_size <= 0 || disp_range <= 0) {
    is_initialized_ = false;return false;}// 灰度数据（左右影像）gray_left_.resize(img_size);gray_right_.resize(img_size);// census数据（左右影像）census_left_.resize(img_size,0);census_right_.resize(img_size,0);// 初始代价数据cost_init_.resize(img_size * disp_range);is_initialized_ = !gray_left_.empty() && !gray_right_.empty() && !census_left_.empty() && !census_right_.empty() && !cost_init_.empty();return is_initialized_;
}

首先，完成一些必要的参数如影像尺寸、视差范围等的赋值。

其次，为左右视图的灰度数据数组分配和图像尺寸等大的空间，用于存储彩色数据转换的灰度数据。为左右视图的Census数据数组分配和图像尺寸等大的空间，用于存储两视图的Census变换值。

最后，为初始代价数组分配尺寸为 $W \times H \times D$ 的空间，用于存储左视图所有像素所有候选视差下的代价值。初始代价还将传递给代价聚合步骤使用。

初始化完成，我们再来看AD-Censu的代价计算步骤：

计算灰度
基于灰度数据计算Census变换数据
计算代价

这三个步骤，我写成三个函数，放在私有函数列表中:

ComputeGray
CensusTransform
ComputeCost

我们一个个介绍：

ComputeGray

彩色数据计算灰度很简单，给R、G、B三个通道分配三个固定的权值，计算三通道的加权和。

gray = r * 0.299 + g * 0.587 + b * 0.114

至于为什么是这三个数字我智能说我忘了，反正用了很久了。

我们看代码：

void CostComputor::ComputeGray()
{
    // 彩色转灰度for (sint32 n = 0; n < 2; n++) {
    const auto color = (n == 0) ? img_left_ : img_right_;auto& gray = (n == 0) ? gray_left_ : gray_right_;for (sint32 y = 0; y < height_; y++) {
    for (sint32 x = 0; x < width_; x++) {
    const auto b = color[y * width_ * 3 + 3 * x];const auto g = color[y * width_ * 3 + 3 * x + 1];const auto r = color[y * width_ * 3 + 3 * x + 2];gray[y * width_ + x] = uint8(r * 0.299 + g * 0.587 + b * 0.114);}}}
}

CensusTransform

Census变换的原理请看：经典SGM：（2）匹配代价计算之Census变换

代码和SGM计算Census变换一样，我就不重复说了，我们直接看代码：

void adcensus_util::census_transform_9x7(const uint8* source, vector<uint64>& census, const sint32& width, const sint32& height)
{
    if (source == nullptr || census.empty() || width <= 9 || height <= 7) {
    return;}// 逐像素计算census值for (sint32 i = 4; i < height - 4; i++) {
    for (sint32 j = 3; j < width - 3; j++) {
    // 中心像素值const uint8 gray_center = source[i * width + j];// 遍历大小为9x7的窗口内邻域像素，逐一比较像素值与中心像素值的的大小，计算census值uint64 census_val = 0u;for (sint32 r = -4; r <= 4; r++) {
    for (sint32 c = -3; c <= 3; c++) {
    census_val <<= 1;const uint8 gray = source[(i + r) * width + j + c];if (gray < gray_center) {
    census_val += 1;}}}// 中心像素的census值census[i * width + j] = census_val;}}
}

ComputeCost

计算代价时，我们遍历左视图每一个像素的每一个候选视差，当左视图像素 $p$ 视差为 $d$ 时，我们可以通过视差公式 $x_r=x_l-d$ 计算出右视图上的同名点坐标，并获取其颜色数据以及Census变换值，颜色数据可以用于计算AD代价，Census变换只可以用于计算Census代价，计算方式请看原理篇：经典AD-Census: （1）代价计算

代码如下：

void CostComputor::ComputeCost()
{
    const sint32 disp_range = max_disparity_ - min_disparity_;// 预设参数const auto lambda_ad = lambda_ad_;const auto lambda_census = lambda_census_;// 计算代价for (sint32 y = 0; y < height_; y++) {
    for (sint32 x = 0; x < width_; x++) {
    const auto bl = img_left_[y * width_ * 3 + 3 * x];const auto gl = img_left_[y * width_ * 3 + 3 * x + 1];const auto rl = img_left_[y * width_ * 3 + 3 * x + 2];const auto& census_val_l = census_left_[y * width_ + x];// 逐视差计算代价值for (sint32 d = min_disparity_; d < max_disparity_; d++) {
    auto& cost = cost_init_[y * width_ * disp_range + x * disp_range + (d - min_disparity_)];const sint32 xr = x - d;if (xr < 0 || xr >= width_) {
    cost = 1.0f;continue;}// ad代价const auto br = img_right_[y * width_ * 3 + 3 * xr];const auto gr = img_right_[y * width_ * 3 + 3 * xr + 1];const auto rr = img_right_[y * width_ * 3 + 3 * xr + 2];const float32 cost_ad = (abs(bl - br) + abs(gl - gr) + abs(rl - rr)) / 3.0f;// census代价const auto& census_val_r = census_right_[y * width_ + xr];const float32 cost_census = static_cast<float32>(adcensus_util::Hamming64(census_val_l, census_val_r));// ad-census代价cost = 1 - exp(-cost_ad / lambda_ad) + 1 - exp(-cost_census / lambda_census);}}}
}

以上我们将代价计算的关键子步骤都实现了，但还需要将这些步骤依次执行，才能得到最终的初始代价计算结果。我们的公有函数Compute就是完成这个工作。实现如下：

void CostComputor::Compute()
{
    if(!is_initialized_) {
    return;}// 计算灰度图ComputeGray();// census变换CensusTransform();// 代价计算ComputeCost();
}

关于代价计算类CostComputor的实现我们就介绍到这里，其他一些未介绍的接口都比较简单，我们就不占篇幅了，大家看完整源码自行理解。

最后该类的使用，我们在主类ADCensusStereo中完成。

首先在主类的初始化函数中，我们自然应该对代价计算类进行初始化：

// 初始化代价计算器
if(!cost_computer_.Initialize(width_,height_,option_.min_disparity,option_.max_disparity)) {
    is_initialized_ = false;return is_initialized_;
}

其次在主类ADCensusStereo的代价计算函数ComputeCost中，我们调用代价计算类CostComputor的相关公有成员函数完成代价计算：

void ADCensusStereo::ComputeCost()
{
    // 设置代价计算器数据cost_computer_.SetData(img_left_, img_right_);// 设置代价计算器参数cost_computer_.SetParams(option_.lambda_ad, option_.lambda_census);// 计算代价cost_computer_.Compute();
}