【计算机网络】物理层 : 编码 ( 模拟信号 编码为 数字信号 | 音频信号 PCM 编码 | 抽样 | 量化 | 编码 | 采样定理 )

一、 模拟数据 编码为 数字信号

---

模拟数据 编码为 数字信号 :

① 计算机数据形式 : 计算机内部的数据都是 二进制数据 ;

② 数字音频 : 计算机内的音频都是 数字音频 ;

③ 音频数字化 : 将 模拟信号的音频 , 通过 采样 , 量化转换 为有限个 数字表示的 离散序列 ;

二、 音频信号 PCM 编码

---

模拟数据 编码为 数字信号 , 最典型的应用 , 就是将 模拟的 音频信号 进行 脉码调制 ( PCM ) 编码 , 转为 数字信号 ;

PCM 音频数据 , 就是 高保真 音频 , 没有经过压缩的原始音频数据 ; 其被存储于 WAV 格式的音频中 ; MP3 , OGG 等格式都是被压缩过的 ;

PCM 编码过程主要有三个步骤 :

① 抽象

② 量化

③ 编码

三、 抽象

---

抽样 : 对 模拟信号 进行 周期性 扫描 , 将 时间上 连续的信号 , 转为 时间上 离散的信号 ;

采样定理 : 为了使所有的离散信号 , 能够 不失真地代表 被抽样的模拟数据 , 需要使用 采样定理 :

$f_{采样频率} \geq 2f_{信号最高频率}$

采样定理 规定了 采样频率 必须 大于等于 信号最高频率的 $2$ 倍 ;

四、 量化

---

量化 :

① 抽样结果 : 抽样取得了 一系列的 电平幅值 集合 ;

② 分级标度 : 将上述 电平幅值 按照一定 分级标度 , 转为对应的数值 , 这些数值取整 ;

③ 离散数值 : 将 连续的 电平幅值 转为 离散的数值 ;

分级标度 示例 :

• 256 种分级 , 对应着每个采样需要使用 $log_2 256 = 8$ 比特来表示 , 对应着 $8$ 位的音频采样 ;
• 65536 种分级 , 对应着每个采样需要使用 $log_2 65536 = 16$ 比特来表示 , 对应着 $16$ 位的音频采样 ;

如 : 音频格式是 44100 Hz , 单声道 , 16 位采样 , 就意味着 , 每个采样的取值有 65536 种 ;

五、 编码

---

编码 : 将 量化的结果 , 转为 二进制编码 ;

六、 采样定理

---

采样定理 : 为了使所有的离散信号 , 能够 不失真地代表 被抽样的模拟数据 , 需要使用 采样定理 :

$f_{采样频率} \geq 2f_{信号最高频率}$

采样定理 规定了 采样频率 必须 大于等于 信号最高频率的 $2$ 倍 ;

模拟信号都是 正弦波 构成的 , 每个模拟信号都可以过滤出一个正弦波 ;

正弦波 $S$ , $1$ 秒有 $2$ 个完整的波形 , 即 $2$ 个波峰 , $2$ 个波谷 , 其周期是 $0.5$ 秒 , 频率是 $2Hz$ ;

正弦波 $B$ , $1$ 秒有 $1$ 个完整的波形 , 即 $1$ 个波峰 , $1$ 个波谷 , 其周期是 $1.0$ 秒 , 频率是 $1Hz$ ;

信号频率就是带宽 , 是 $1$ 秒钟震荡的次数 , $S$ 信号波形 频率 $2Hz$ , $B$ 信号波形 频率 $1Hz$ ;

针对 $B$ 波形 , 确定采样频率 :

• 正弦波的公式 : $y = A sin( \omega t + \phi )$

• 已知参数 : 其中的 $\omega$ 就是频率 , $1Hz$ ;

• 未知参数 : 还剩下未知数 $A$ 和 $\phi$ ;

• 未知参数求值条件 : 只要代入两组数据 , 就可以将该正弦函数的公式求出 , 因此采样时 , 采两组数据 , 就能完全还原该正弦函数 ;

采样定理 结论 :

• 在一个 正弦波周期内 , 采样 $2$ 次 , 就可以还原该正弦波 ;

• 如果 $1$ 秒钟有 $1$ 个完整的正弦波 , 那么采样 $2$ 次即可 ;

• 如果 $1$ 秒钟有 $2$ 个完整的正弦波 , 那么采样 $2 \times 2 = 4$ 次即可 ;

• 因此采样定理中规定 , 采样频率 必须 大于等于 2倍信号最高频率 ;

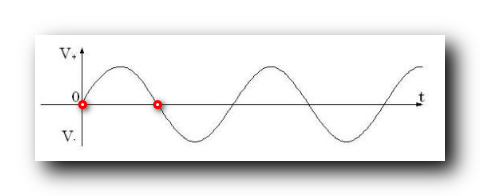
也可以采更多的样本 , 采样频率越高 , 正弦波形恢复的更准确 , 就越不容易失真 ;

如 : 音频的采样 $44100Hz$ , $48000 Hz$ , $96000 Hz$ , 都非常大 ;

人耳能听到的声音是 $20Hz$ ~ $20000Hz$ , 如果让人耳能够听不出来区别 , 必须在 $20000 \times 2 = 40000 Hz$ 以上的采样率才能达到最基本 高保真 要求 ;

高频失真 , 就是高频的波形没有完整的还原出来 , 采样率不足导致的 ;