奇异值分解（SVD）及其应用

奇异值分解的定义

SVD（Singular Value Decomposition）可以理解为：将一个比较复杂的矩阵用更小更简单的3个子矩阵的相乘来表示，这3个小矩阵描述了大矩阵重要的特性。

定义：矩阵的奇异值分解是指将一个秩为 $r$的实矩阵 $A_{m \times n}$分解为三个实矩阵乘积的形式：

$A_{m\times n} = U_{m \times m} \Sigma_{m \times n} V ^ { T }_{n\times n} \approx U_{m \times k} \Sigma_{k \times k} V ^ { T }_{k\times n}$

其中 $U$是 $m$阶正交矩阵（ $U$的列向量称为左奇异向量）， $V$是 $n$阶正交矩阵（ $V$的列向量称为右奇异向量）， $\Sigma$是 $m \times n$矩形对角矩阵，称为奇异值矩阵，对角线上的元素称为奇异值。

$\Sigma = \begin{bmatrix} D_{r\times r}&0\\ 0&0\\ \end{bmatrix}_{m\times n}$

$D$是一个 $r \times r$的对角阵， $D$的对角线元素是 $A$的前 $r$个奇异值 $\sigma _ { 1 } \geq \sigma _ { 2 } \geq \cdots \geq \sigma _ { r } > 0$（非负，降序）。

知识点：任意一个实矩阵 $A$可以由其外积展开式表示

$A = \sigma _ { 1 } u _ { 1 } v _ { 1 } ^ { T } + \sigma _ { 2 } u _ { 2 } v _ { 2 } ^ { T } + \cdots + \sigma _ { r } u _ { r } v _ { r } ^ { T }$

其中 $u _ { k } v _ { k } ^ { T }$为 $m \times n$矩阵，是列向量 $u _ { k }$和行向量 $v _ { k } ^ { T }$的外积， $\sigma _ { k }$为奇异值， $u _ { k } , v _ { k } ^ { T } , \sigma _ { k }$通过矩阵 $A$的奇异值分解得到。

知识点：奇异值在矩阵中按照从大到小排列，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。我们可以用最大的 $k$个奇异值的矩阵和 $UV^T$相乘来近似描述矩阵，从而实现了降维、减少数据存储、提升计算性能等效果。

奇异值分解的计算

设矩阵 $A$的奇异值分解为 $A = U \Sigma V ^ { T }$，则有

$\begin{array} { l } { A ^ { T } A = V ( \Sigma ^ { T } \Sigma ) V ^ { T } } \\ { A A ^ { T } = U ( \Sigma \Sigma ^ { T } ) U ^ { T } } \end{array}$

即对称矩阵 $A^TA$和 $AA^T$的特征分解可以由矩阵 $A$的奇异值分解矩阵表示。

证明： $A^TA$的特征值非负。

令 $A$是 $m \times n$矩阵，那么 $A^TA$是对称矩阵且可以正交对角化，让 $\{v_1,\dots,v_n\}$是 $R^n$的单位正交基且构成 $A^TA$的特征向量， $\lambda_1,\dots,\lambda_n$是 $A^TA$对应的特征值，那么对 $1\le{i}\le{n}$，

$\| Av_i \|^2 = (Av_i)^T(Av_i)=v_i^TA^TAv_i =v_i^T\lambda_iv_i=\lambda_i$

所以 $A^TA$的所有特征值都非负，如果必要，通过重新编号我们可以假设特征值的重新排列满足

$\lambda_ { 1 } \geq \lambda_ { 2 } \geq \cdots \geq \lambda_ { n } \geq 0$

$A$的奇异值是 $A^TA$的特征值的平方根，记为 $\sigma_1,\sigma_2,\dots,\sigma_n$，且它们递减顺序排列。

$\sigma _ { j } = \|Av_j \| = \sqrt { \lambda _ { j } }, \quad j = 1,2 , \cdots , n$

可见，对 $A$进行奇异值分解需要求矩阵 $A^TA$的特征值及其对应的标准正交的特征向量来构成正交矩阵 $V$的列，特征值 $\lambda _ { j }$的平方根得到奇异值$\sigma _ { i } $也即得到奇异值矩阵$\Sigma$。

证明：假设 $\{v_1,v_2,\dots,v_n\}$是包含 $A^TA$特征向量的 $R^n$上的标准正交基，重新整理使得对应 $A^TA$的特征值满足 $\lambda_1 \ge \lambda_2 \ge \dots \ge \lambda_n$。若 $A$有 $r$个非零奇异值，则 $\{Av_1,Av_2,\dots,Av_r\}$是 $ColA$的一个正交基，且 $rank A = r$。

当 $i$不等于 $j$时， $v_i^Tv_j=0$。

$(Av_i)^TAv_j = v_i^TA^TAv_j = \lambda_jv_i^Tv_j = 0$

所以， $\{Av_1,Av_2,\dots,Av_n\}$是一个正交基。由于向量 $Av_1,Av_2,\dots,Av_n$的长度是 $A$的奇异值，且因为有 $r$个非零奇异值， $Av_i (r\ge i\ge 1)$为非零向量。所以 $Av_1,Av_2,\dots,Av_r$线性无关，且属于 $ColA$。

对任意属于 $ColA$的 $y$，如 $y=Ax$，我们可以写出 $x=c_1v_1+\dots+c_nv_n$，且

$y = Ax = c_1Av_1+\dots+c_rA_rv_r$

这样， $y$在 $Span\{Av_1,\dots,Av_r\}$中，这说明 $\{Av_1,Av_2,\dots,Av_r\}$是 $ColA$的一个正交基，因此 $rank A = dim(ColA)=r$。

由于 $\{Av_1,Av_2,\dots,Av_r\}$是 $ColA$的一个正交基，将每一个 $Av_i$单位化得到一个标准正交基 $\{u_1,u_2\dots u_r\}$，此处

$u_i = \frac{1}{\|Av_i\|}Av_i = \frac{1}{\sigma_i}Av_i（r\ge i\ge1）$

将 $\{u_1,u_2\dots u_r\}$扩充为 $R^m$的单位正交基 $\{u_1,u_2\dots u_m\}$。

取

$U=(u_1,u_2,\dots,u_m),V=(v_1,v_2,\dots,v_n)$

由构造可知， $U$和 $V$是正交矩阵，

$AV=(Av_1,\dots,Av_r,0,\dots,0)=(\sigma_1u_1,\dots,\sigma_ru_r,0\dots,0)=U\Sigma$

即： $A=U \Sigma V^T$，从而得到 $U$。

知识点：任意给定一个实矩阵，其奇异值分解一定存在，但并不唯一。

---

奇异值分解的实现

1. 手动实现

# 实现奇异值分解， 输入一个numpy矩阵，输出 U, sigma, V
import numpy as np# 基于矩阵分解的结果，复原矩阵
def rebuildMatrix(U, sigma, V):a = np.dot(U, sigma)a = np.dot(a, np.transpose(V))return a# 基于特征值的大小，对特征值以及特征向量进行倒序排列。
def sortByEigenValue(Eigenvalues, EigenVectors):index = np.argsort(-1 * Eigenvalues)Eigenvalues = Eigenvalues[index]EigenVectors = EigenVectors[:, index]return Eigenvalues, EigenVectors# 对一个矩阵进行奇异值分解
def SVD(matrixA, NumOfLeft=None):# NumOfLeft是要保留的奇异值的个数，也就是中间那个方阵的宽度# 首先求transpose(A)*AmatrixAT_matrixA = np.dot(np.transpose(matrixA), matrixA)# 然后求右奇异向量lambda_V, X_V = np.linalg.eig(matrixAT_matrixA)lambda_V, X_V = sortByEigenValue(lambda_V, X_V)# 求奇异值sigmas = lambda_V# python里很小的数有时候是负数sigmas = list(map(lambda x: np.sqrt(x) if x > 0 else 0, sigmas))sigmas = np.array(sigmas)sigmasMatrix = np.diag(sigmas)if NumOfLeft is None:# 大于0的特征值的个数rankOfSigmasMatrix = len(list(filter(lambda x: x > 0, sigmas)))else:rankOfSigmasMatrix = NumOfLeft# 特征值为0的奇异值就不要了sigmasMatrix = sigmasMatrix[0:rankOfSigmasMatrix, :]# 计算左奇异向量# 初始化一个左奇异向量矩阵，这里直接进行裁剪X_U = np.zeros((matrixA.shape[0], rankOfSigmasMatrix))for i in range(rankOfSigmasMatrix):X_U[:, i] = np.transpose(np.dot(matrixA, X_V[:, i]) / sigmas[i])# 对右奇异向量和奇异值矩阵进行裁剪X_V = X_V[:, 0:rankOfSigmasMatrix]sigmasMatrix = sigmasMatrix[0:rankOfSigmasMatrix, 0:rankOfSigmasMatrix]return X_U, sigmasMatrix, X_VA = np.array([[4, 11, 14], [8, 7, -2]])
X_U, sigmasMatrix, X_V = SVD(A)
print(A)
# [[ 4 11 14]
# [ 8 7 -2]]print(X_U.shape)  # (2, 2)
print(sigmasMatrix.shape)  # (2, 2)
print(X_V.shape)  # (3, 2)
print(rebuildMatrix(X_U, sigmasMatrix, X_V))
# [[ 4. 11. 14.]
# [ 8. 7. -2.]]

2. 使用numpy.linalg.svd函数

import numpy as npA = np.array([[4, 11, 14], [8, 7, -2]])
print(A)
# [[ 4 11 14]
# [ 8 7 -2]]u, s, vh = np.linalg.svd(A, full_matrices=False)
print(u.shape)  # (2, 2)
print(s.shape)  # (2,)
print(vh.shape)  # (2, 3)a = np.dot(u, np.diag(s))
a = np.dot(a, vh)
print(a)
# [[ 4. 11. 14.]
# [ 8. 7. -2.]]

---

奇异值分解的应用

1. 数据压缩

奇异值分解可以有效地表示数据。例如，假设我们希望传输下面的图像，它由一个 $25\times 15$个黑色或白色像素组成的数组。

由于此图像中只有三种类型的列，如下图所示，因此可以用更紧凑的形式表示数据。

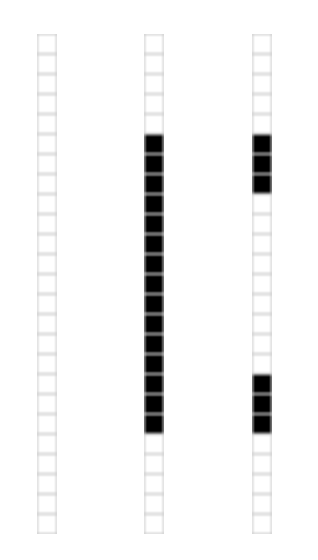
我们将图像表示为一个 $25\times 15$矩阵，矩阵的元素对应着图像的不同像素，如果像素是白色的话，就取 1，黑色的就取 0。 我们得到了一个具有375个元素的矩阵，如下图所示

如果对 $M$进行奇异值分解，我们会发现只有三个非零奇异值 $\sigma_1=14.72,\sigma_2=5.22,\sigma_3=3.31$（非零奇异值的数目等于矩阵的秩，在这个例子中，我们看到矩阵中有三个线性无关的列，这意味着秩将是3）。

$M = \sigma _ { 1 } u _ { 1 } v _ { 1 } ^ { T } + \sigma _ { 2 } u _ { 2 } v _ { 2 } ^ { T } + \sigma _ { 3 } u _ { 3 } v _ { 3 } ^ { T }$

$v_i$具有15个元素， $u_i$ 具有25个元素， $\sigma_i$ 对应不同的奇异值。我们就可以用123个元素来表示具有375个元素的图像数据了。通过这种方式，奇异值分解可以发现矩阵中的冗余，并提供消除冗余的格式。

2. 去噪

前面的例子展示了如何利用许多奇异值为零的情况。一般来说，大的奇异值对应的部分会包含更多的信息。假设我们使用扫描仪将此图像输入计算机。但是，我们的扫描仪会在图像中引入一些缺陷（通常称为“噪声”）。

我们可以用同样的方法进行：用一个 $25\times 15$矩阵表示数据，并执行奇异值分解。我们发现以下奇异值：

$\sigma_1=14.15,\sigma_2=4.67,\sigma_3=3.00,\sigma_4=0.21,\dots,\sigma_{15}=0.05$

显然，前三个奇异值是最重要的，所以我们假设其它的都是由于图像中的噪声造成的，并进行近似。
$M \approx \sigma _ { 1 } u _ { 1 } v _ { 1 } ^ { T } + \sigma _ { 2 } u _ { 2 } v _ { 2 } ^ { T } + \sigma _ { 3 } u _ { 3 } v _ { 3 } ^ { T }$

这导致下面的改进图像。

3. 数据分析

我们搜集的数据中总是存在噪声：无论采用的设备多精密，方法有多好，总是会存在一些误差的。如果你们还记得上文提到的，大的奇异值对应了矩阵中的主要信息的话，运用SVD进行数据分析，提取其中的主要部分的话，还是相当合理的。

假设我们收集了一些数据，如下所示：

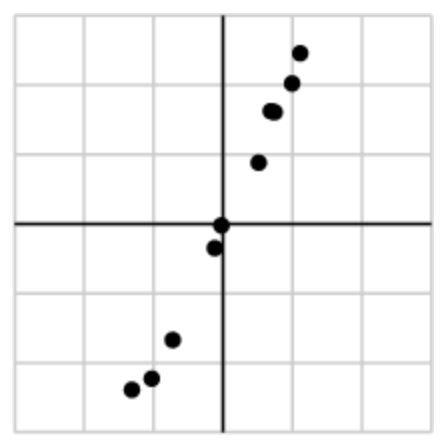
我们可以将数据放入矩阵中：

$\begin{bmatrix} -1.03& 0.74 &-0.02 &0.51 &-1.31 &0.99 &0.69 &-0.12 &-0.72 &1.11\\ -2.23 &1.61 &-0.02 &0.88 &-2.39 &2.02 &1.62 &-0.35 &-1.67 &2.46\\ \end{bmatrix}$

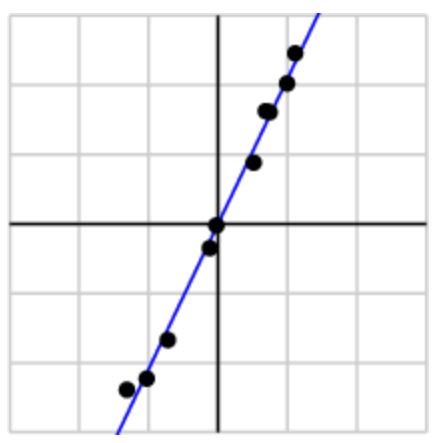
经过奇异值分解后，得到 $\sigma_1=6.04,\sigma_2 = 0.22$。

由于第一个奇异值远比第二个要大，可以假设 $\sigma_2$的小值是由于数据中的噪声产生的，并且该奇异值理想情况下应为零。在这种情况下，矩阵的秩为1，意味着所有数据都位于 $u_i$定义的行上。

---

参考文献

• https://zhuanlan.zhihu.com/p/54693391
• http://www.ams.org/publicoutreach/feature-column/fcarc-svd

---