原题链接:https://codeforces.com/contest/1393/problem/D
题意:给定一个 的字符矩阵,判断有多少个相同字符斜正方形。
解题思路:我们首先不管别的,对于每一个字符,它都能组成只有一个相同字符的斜正方形。那么其余的就是多种相同字符组合在一起形成的斜正方形了,怎么组合呢?我们不难发现。
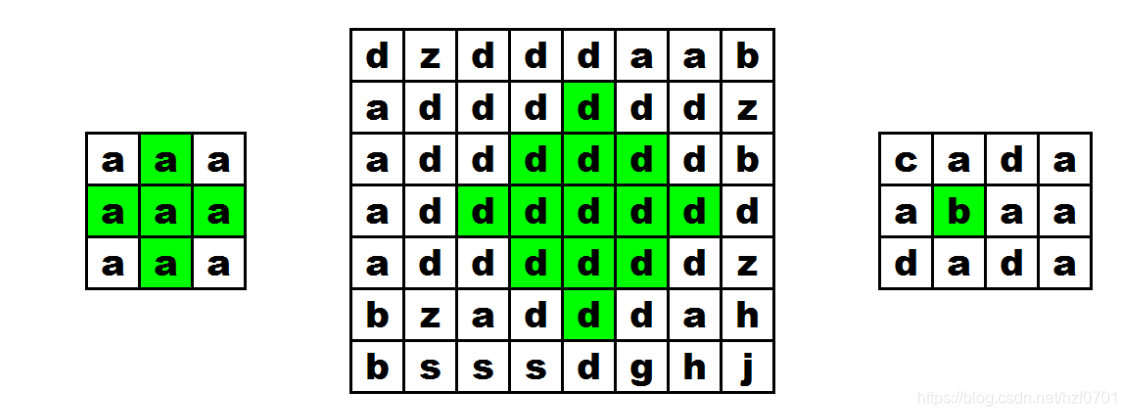
仔细看这张图,在第一个图形中,若要构成这样的斜正方形,那么最下面的那个点一定要可以往上延伸。即判断当前位置[i][j]与上面四个位置([i-1][j]、[i-1][j-1]、[i-1][j+1]、[i-2][j])能否形成“斜正方形”,那么我们再看第二张图,从最下面那个点开始往上延伸,我们发现这些是有规律的,即是一个动态规划的过程,若我们设最下面那个点的方案数为dp[i][j],那么这个值本身就有一个1,就是自己单独形成一个字符,那么还有呢?就是可以和上面四个字符形成一个斜正方形或者更大,那么我只要它们字符都相等,不就满足了吗?那怎么写动态规划方程呢?我们就要知道这个点的方案数由哪几个点维护?就是由[i-1][j-1]、[i-1][j+1]、[i-2][j]这三个点维护,那你可能就会问呢?组合不是与四个点组合吗?为什么只要考虑三个点,因为不管怎样,在那三个点的维护下,最中间那个点已经被维护了,若三个点向上延伸也能组成一个斜正方形,那么你画一下图,最中间那个点根本不用考虑。所以我们就可以写出动态转移方程了,既然是由三个点维护,那肯定是要取三个点的最小值的。故:
dp[i][j]=min(min(dp[i-1)[j-1],dp[i-1][j+1],dp[i-2][j])+1//加上1是它自己本身就有一,我们也可以一开始就都初始化为1.我们具体看代码。
AC代码 :
/* *邮箱:2825841950@qq.com *blog:https://blog.csdn.net/hzf0701 *注:代码如有问题请私信我或在评论区留言,谢谢支持。 */
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<stack>
#include<queue>
#include<cstring>
#include<map>
#include<iterator>
#include<list>
#include<set>
#include<functional>
#include<memory.h>//低版本G++编译器不支持,若使用这种G++编译器此段应注释掉
#include<iomanip>
#include<vector>
#include<cstring>
#define scd(n) scanf("%d",&n)
#define scf(n) scanf("%f",&n)
#define scc(n) scanf("%c",&n)
#define scs(n) scanf("%s",n)
#define prd(n) printf("%d",n)
#define prf(n) printf("%f",n)
#define prc(n) printf("%c",n)
#define prs(n) printf("%s",n)
#define rep(i,a,n) for (int i=a;i<=n;i++)//i为循环变量,a为初始值,n为界限值,递增
#define per(i,a,n) for (int i=a;i>=n;i--)//i为循环变量, a为初始值,n为界限值,递减。
#define pb push_back
#define fi first
#define se second
#define mp make_pair
using namespace std;
const int inf = 0x3f3f3f3f;//无穷大
const int maxn = 2e3+2;//最大值。
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> pll;
typedef pair<int, int> pii;
//*******************************分割线,以上为代码自定义代码模板***************************************//char graph[maxn][maxn];//代表给定的矩阵。
ll dp[maxn][maxn];//dp[i][j]代表它的方案数。也为位置[i][j]向上能最多”延伸“的”斜正方形边长“
int n,m;//n行m列。
void solve(){int i,j;for(i=0;i<n;i++)cin>>graph[i];ll ans=0;//统计方案数。for(i=0;i<n;i++){for(j=0;j<m;j++){dp[i][j]=1;//每个点都有它自己一个人组成的方案数。//进行判断,是否可以增加,也就是延伸。 ,延伸分别是对上面四个位置延伸。先判断有没有越界。if(i>1&&j>0&&j<m-1&&graph[i][j]==graph[i-1][j]&&graph[i][j]==graph[i-2][j]&&graph[i][j]==graph[i-1][j-1]&&graph[i][j]==graph[i-1][j+1])dp[i][j]+=min(min(dp[i-1][j-1],dp[i-1][j+1]),dp[i-2][j]);ans+=dp[i][j];}}cout<<ans<<endl;
}
int main(){//freopen("in.txt", "r", stdin);//提交的时候要注释掉ios::sync_with_stdio(false);//打消iostream中输入输出缓存,节省时间。cin.tie(0); cout.tie(0);//可以通过tie(0)(0表示NULL)来解除cin与cout的绑定,进一步加快执行效率。while(cin>>n>>m){solve();}return 0;
}