一、简介
Finite State Transducers 简称 FST, 中文名:有穷状态转换器。FST目前在语音识别和自然语言搜索、处理等方向被广泛应用。
例如,在自然语言处理中,经常会遇到一些针对某些内容法则做出修改的操作,比如:如果c的后面紧接x的话,则把c变为b,FST则是基于这些规则上的数学操作,来把若干个规则整合成一个单程的大型规则,以有效提高基于规则的系统(rule-based system)的效率。
其功能类似于字典的功能(STL 中的map,C# 中的Dictionary),但其查找是O(1)的,仅仅等于所查找的key长度。目前Lucene4.0在查找Term时就用到了该算法来确定此Term在字典中的位置。
FST 可以表示成FST<Key, Value>的形式,我们可以用O(length(key))的复杂度,找到key所对应的值。除此之外,FST 还支持用Value来查找key以及查找Value最优的key等功能。在查找最优的Value时,会用到求最短路径的Dijikstra算法,但建图过程与此无关。
二、相关概念
有限自动机(Finite Automata, FA) 是由一组有限的状态和状态转移的集合组成,其每一个转移都至少有一个标签。最基本的FA是有限状态接收器(Finite State Acceptor,FSA)。对于给定的输入序列,FSA返回“接收”或者“不接收”两种状态。
图1(a)是一个FSA的示例,其节点和弧分别对应状态与状态的转移。例如,FSA可通过0,1,1,2,5接收一个符号序列“a,b,c,d”,但是无法接收到“a,b,d”序列,因此FSA表示了一组能被接收到的符号序列集合。图1(a)的FSA对应于正则表达式ab*cd|bcd*。我们假设状态0代表初始状态,状态5代表终止状态,如果不特别指出,本文中粗线单线圆代表初始状态,细线双线圆代表终止状态。
有限状态转移器(Finite State Transducers, FST) 是FSA的扩展,其每一次状态转移时都有一个输出标签,叫做输入输出标签对,如图1(b)就是一个FST的例子。通过这样的标签对,FST可描述一组规则的转换或一组符号序列到另一组符号序列的转换。图1(b)的FST将符号序列“a,b,c,d”转换为另一个符号序列“z,y,x,w”。
加权有限状态接收机(Weighted Finite-State Acceptors, WFSA) 在每一次状态转移时都有一个权重,在每次的初始状态都有初始权重,在每次的终止状态都有终止权重,权重一般是转移或初始/终止状态的概率或损失,权重会延每条路径进行累积,并在不同路径进行累加。图1(c)是一个WFSA的例子,每次状态转移的权重表示为“输入-标签/权重”,而初始和终止状态的权重表示为“状态 数量/权重”,在上图中,初始状态0的初始权重为0.5,终止状态5的终止权重为0.1。例如,上图中的WFSA沿着转移状态“0,1,1,2,5”以累积权重0.51.20.732*0.1=0.252接收到一个序列“a,b,c,d”。
加权有限状态转移器(Weighted Finite-State Transducers, WFST) 在每次状态转移时同时具有输出标签和权重,同时具有FST和WFSA的特性,图1(d)是一个WFST的例子,这里每次的状态转移标签都以“输入-标签: 输出-标签/权重”的形式进行转移,初始和终止状态也相应的分类了权重。在该图中的WFST,将符号序列“a,b,c,d”以0.252的累积权重转换为序列“z,y,x,w”。
WFST通过一个8元组 (∑,Λ,Q,I,F,E,λ,ρ) 定义:
(1) ∑ 是一组有限的输入标签;
(2) Λ 是一组有限的输出标签;
(3) Q 是一组有限的状态;
(4) I?Q 是一组初始状态;
(5) F?Q 是一组终止状态;
(6) E?Q×(∑∪{?})×K×Q 是多组有限的转移;其中" ? "是一个元符号标签,它代表了无符号的输入输出;K 是一组权重元素集合;
(7) λ:I→K 是权重初始函数;
(8) ρ:F→K 是权重终止函数;
通过以上定义,图1(d)的WFST可以被定义如下:
(1) ∑={a,b,c,d,e}
(2) Λ={v,x,y,w,z}
(3) Q={0,1,2,3,4,5}
(4) I={0}
(5) F={5}
(6) E={(0,a,z,1.2,1),(0,b,y,0.8,3),(1,b,y,0.7,1),(1,c,x,3,2),(2,d,w,2,5),(3,c,x,0.2,4),(4,d,w,1.2,4),(4,e,v,0.6,5)}
(7) λ(0)=0.5 (8) ρ(5)=0.1
其中 E 中的每次转移由(源状态,输入标签,输出标签,权重,目标状态)组成,可以从以上描述中可知,FSA, FST, WFSA都是WFST的特殊形式,这些形式也可以由上述相似的元组表示。
三、创建和存储FST举例
为了让大家对FST有一个初步的认识,我们举一个简单的例子来进行说明。
我们假设创建一组映射:
Key → Value
“cat” - > 5,
“deep” - > 10,
“do” - > 15,
“dog” - > 2,
“dogs” - > 8,
对于经典FST算法来说,要求Key必须按字典序从小到大加入到FST中,原因主要是因为在处理大数据的情况下,我们不太可能把整个FST数据结构都同时放在内存中,而是要边建图边将建好的图存储在外部文件中,以便节省内存。所以我们第一步要对所有的Key排序,对于我给这个例子来说,已经保证了字典序的顺序。
根据此例子的输入我们可以建立下图所示的FST:
(注意这个图上的label应该指在a头上)
从上图可以看出,每条边有两条属性,一个表示label(key的元素),另一个表示Value(out)。注意Value不一定是数字,还可一是另一个字符串,但要求Value必须满足叠加性,如这里的正整数2 + 8 = 10。字符串的叠加行为: aa + b = aab。
建完这个图之后,我们就可以很容易的查找出任意一个key的Value了。例如:查找dog,我们查找的路径为:0 → 4 → 8 → 9。 其权值和为: 2 + 0 + 0 + 0 = 2。其中最后一个零表示node[9].finalOut = 0。所以“dog”的Value为2。再例如:查找do,我们查找的路径为:0 → 4 → 8。其权值和为:2+0+13=15。其中最后13表示node[8].finalOut = 13。
到这里,我们已经对FST有了一个感性的认识,下面我们详细讨论FST的建图过程:
1,建一个空节点,表示FST的入口,所有的Key都从这个入口开始。
2, 如果还有未处理的Key,则枚举Key的每一个label。
处理流程如下:
如果当前节点存在含此label的边,则如果Value包含该边的out值,则Value = Value – out否则令temp=out–Value;out =Value并使下一个节点的所有边out都加上temp。如果下一节点是Final节点 则FinalOut += temp进入下一个节点
否则: 新建一个节点令其out = Value, Value = 0。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
如果此处有点不太明白,请看上文中例子的构建过程:



通过上面的算法我们看到,FST 本身并不要求输入要按照字典序从小到大,但正如我文章开头说的那样,FST只是一个映射,只能成为我们应用程序的一个工具,所以决不能让这个工具占用我们过多宝贵的内存空间,因此我们要把不用的节点存入到文件中。但是我们的问题是什么样的节点才是不要的节点呢,要解决这个问题还得回顾我们刚才的算法流程。
我们发现存储cat字符串的三个节点自从开始处理deep后就在也没用到过,这是巧合么?如果这是个巧合,那么当开始处理do后就再也没用到过存储eep的三个节点,这是巧合么?如果不是巧合,那到底是什么原因呢?很明显是字典序在做怪!!
正因为,我们保证了所有的Key都是按照字典序加进来的,所以当加入一个新Key的时侯,我们可以先求出新加的Key和上一次输入的Key的公共前缀,然后就可以把 上一次输入的Key除去公共前缀剩下的部分存入文件中了。
综上,可知FST是强大的,但内存是有限的,导致我们必须保证输入有序。
四、在NLP中的FST的创建举例
FST在一些NLP task里面特别有用,比如说我给出以下三个规则:
- 当c后紧接x时,将c变为b cx→bx
- 当a前面是rs时,将a变为b rsa→rsb
- 当b前面是rs,后面是xy时,将b变为a rsbxy→rsaxy
所以当我们的input string是rsaxyrscxy时,根据以上三个规则,我们就可以做出以下的变换:
rsaxyrscxy→rsaxyrsbxy rsaxyrsbxy→rsbxyrsbxy rsbxyrsbxy→rsaxyrsaxy
然后大家就会发现,第二步做的变换的第三步又变回去了!于是FST就出现了,FST提供了一种消除这些低效的方法。
首先把每一个rule都用一个FST表示出来,每个状态间的连线的属性表示接收input character以及相应的output character. 表示方式是input/output. 所以针对上面的3个rules,我们可以得到以下三个FST: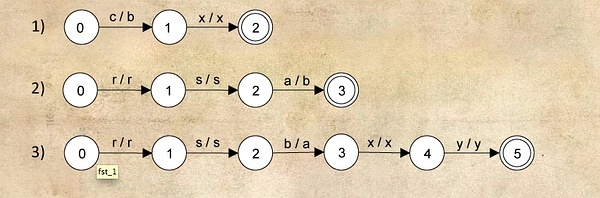
接下来,为了让FST能适用于任何任意长度的字符串而且能够根据规则进行必要的操作,我们就要extend FST.
以刚刚的rule 1为例,他只是为了变换cx到bx,但是他也要能handle得了其前面的‘rsaxyrs’这些characters还有他后面的那个y,所以,我们可以简单的把这些貌似与规则暂时无关的characters列在一个its own individual edge上面, 标注为?/?,然后用ε表示无输出。我们来看一下刚刚那三个FST扩展后的结果:
以第一个图为例,首先输入rsaxyrscxy,然后c前面的这一串‘rsaxyrs’,由于他们和我规则没有关系,所以他们是什么就还是什么,然后遇到c字符了,我们就用c/ε 来表示“暂时无输出,跳入下一个字符”,所以我们看到了1那个节点,这个节点分别有三个link指出去,,x/bx表示输入x的话,那就输出bx;?/c?表示输入为非x外的任意字符,则原样输出(即输出c和该字符本身);c/c表示输入c,输出c(相当于继续判断我后面那个是什么)。
得到各个规则扩展的FST之后,就要去合成一个single FST了,对FST合成算法的完整解释超出了本文的范围,在本例中通过简单合并可以得到下面这个composed FST:
这个final FST能达到那三个rule的效果,而且重点是转换只需要通过FST进行一次遍历,并没有导致任何低效的转换。 原先这些规则的任务耗费的时间与规则数量、窗长、输入字符数都有关系,而现在FST耗费的时间只与input string字符数有关了。
参考网址:
Finite State Transducers 详解
语音识别解码器(1)—自动机与半环
工作笔记:Finite State Transducer(FST)in NLP
对于WFST在语音识别中的应用,可以参考这两个系列:
走进语音识别中的WFST(一)
语音识别解码器(1)—自动机与半环
和
Speech Recognition Algorithms Using Weighted Finite-State Transducers
这本书