Towards quantum machine learning with tensor networks(基于张量网络的机器学习研究)

虽然本人这一个多星期停更了，但是只有鬼知道我这两个星期经历了什么，我从今年的三月份开始正式写博客，本来出发点是一边记录自己的大学课外的学习历程（虽然我才大一），一边进行深度科普，让更多的小伙伴们真正的从入门开始了解量子，熟悉量子，热爱量子，前面半年，我从大一的线性代数到初入量子世界（线代是量子的数学语言），再到后面的量子计算入门，紧接着的就是张量，机器学习，张量分解，张量网络，很多时候我会疑惑 ，机器学习和量子有什么关系，随着学的东西越来越多，眼界越来越开阔，我发现这些都是我们最敬爱的小红的老师为我们的基础在铺垫，那么现在，不敢说基础有多么的好，但是面对这些原本在我看来只是远在天边高大上的 科研知识，也是不再那么的胆怯畏惧了，在老师的 “逼迫打压” 之下，一次又一次的突破自己，这篇博客主要内容就是我这个两个星期学习的一篇论文，当然，这也是我看的第一篇论文 ，自然也是磕磕碰碰，下面我将和大家一起来享受科学的甘霖：

在学习这篇论文之前，必须要有简单的基础铺垫，传送门一， 传送门二，希望您能看懂！

论文再现：猛戳这里_φ(?_?? 人丑就要多读书

论文简要：

机器学习是量子计算的一种很有前途的应用，但由于近期设备的物理量子比特数量有限，错误率很高，因此在今天的实施中仍然存在挑战。基于张量网络在经典环境下对机器学习的有用性，我们提出了基于树和矩阵乘积态张量网络的电路，用于区分学习和生成性学习的量子计算方法，这些方法可能已经对这样的近期设备产生了好处。在此基础上，我们提出了基于树和矩阵乘积态张量网络的电路的量子计算方法，用于区分学习和生成性学习。结果是一个统一的框架，在这个框架中，经典和量子计算可以从相同的理论和算法发展中受益，相同的模型可以被经典地训练，然后转移到量子环境中进行额外的优化。张量网络电路还可以提供量子比特高效方案，其中，根据体系结构，所需的物理量子比特的数量仅与输入或输出数据大小成对数比例，或者与输入或输出数据大小无关。我们用数值实验来演示该建议，使用目前可以在量子硬件上执行的混合量子-经典优化过程来训练用于执行手写识别的判别模型，并测试训练模型的抗噪能力。

一 . 图片像素的量子态表示

我们知道对于一张图片来说，无论是高清的还是低画质的，组成他们的都是数以万计 的像素点，传统计算机在处理这些像素点的方法都是依赖 传统的电子比特，那么在量子计算机中，我们对于像素的表达 用的便是 量子比特！这句话蕴含的东西就多了去了！

如何编码像素数据？如何表达像素？如何将量子比特与像素数据对应起来？如何批量操作处理？

要引入基于张量网络的监督学习模型。我们需要解决的第一个问题是如何把图片集输入到张量网络中去。在机器学习领域,图片通常被表示为一个维度为像素个数 $N$ 的矢量。矢量的每个元素值对应各个像素的值。而在张量网络中,假设物理腿的维度为 $d$ ,那 $N$ 个物理腿的张量网络对应到一个维度为 $d^{N}$ 的矢量。

那么在构造张量网络监督学习模型时,如果我们希望用一个物理腿来作为一个图片像素的输入的话。我们就需要首先定义一个从 $N$ 维空间到 $d^{N}$ 维空间的特征映射，具体来说，我们可以把每个像素看做是一个独立的状态，每个像素值先通过一个特征映射 $\phi$ 对应到一个局域的状态矢量。然后 $N$ 个独立系统的状态可以用各个局域状态矢量的张量积构造。

看图举例子这种方法从某种意义上推动了人类文明的进步：

我们先对21世纪物欲纵横的科技享受 忆苦思甜，回忆上世纪七八十年代，家里有一台黑白电视机那绝对是万元户级别的！黑白电视机里面放的肯定是黑白图片啦，唉，我们这里就以黑白图片为例！

看上图，每一个小方格代表一个像素点，显然，这个黑白图片的大小是4x4的，我们为了用后面用单自旋量子态表示每个像素（可能你不太理解，不用管），所以采用独热编码的方式标记这些像素，又因为本来就是黑白图片，对于黑色的，我们直接用 [1,0] 表示，白色的像素点，我们用 [0,1] 表示，所以，中间地带的灰色像素，我们就用他们二者的叠加态来表示！

所以这个图片，我们通常叫它 灰度图像！

这就把问题简单化了，我们可以直接迁移到薛定谔的猫上的那个叠加态，生和死这两个基态就是这里的黑与白，既生又死的叠加态就是这里的灰色地带！所以，到了这里，我们就可以用一个量子的自旋态来表示
像素数据了：

这里只举例了6个像素的图片， $s_{1},s_{2} \cdots s_{6}$ 中每一个 $s_{j}$的指标是从 1 到 $d$，其中 $d$ 也就是它对应的特征映射的维度 ，下面一排也就是其对应的不同系数的单自旋量子叠加态！而这个大写的 $\Phi$ 就一个整体的映射的过程，是一个将像素数据映射到量子态的过程，下面是其映射的数学表达：

单个像素数据的映射函数为：
$\phi\left(x_{j}\right)=\left[\cos \left(\frac{\pi}{2} x_{j}\right), \sin \left(\frac{\pi}{2} x_{j}\right)\right] \quad x_{j} \in[0,1]$
多个结合之后：

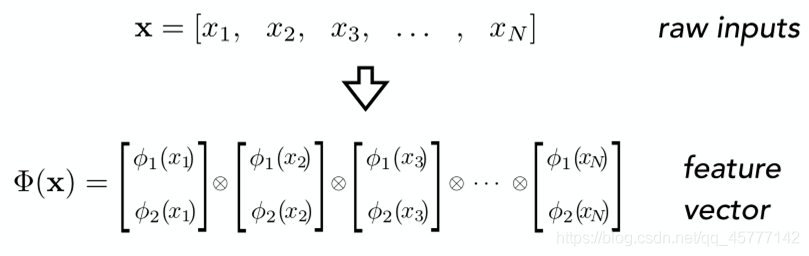
这里的 x 代表的是所有像素数据的结合， $x_{j}$ 代表的就是每一个像素数据，我们用一个整体的集合来表示。所有的单个像素映射之后用直积对的形式给他们结合在一起！最后，联立上面的公式，就可以得到一个完整的映射函数：

$\mathbf{x} \rightarrow|\Phi(\mathbf{x})\rangle=\left[\begin{array}{c} \cos \left(\frac{\pi}{2} x_{1}\right) \\ \sin \left(\frac{\pi}{2} x_{1}\right) \end{array}\right] \otimes\left[\begin{array}{c} \cos \left(\frac{\pi}{2} x_{2}\right) \\ \sin \left(\frac{\pi}{2} x_{2}\right) \end{array}\right] \otimes \cdots \otimes\left[\begin{array}{c} \cos \left(\frac{\pi}{2} x_{N}\right) \\ \sin \left(\frac{\pi}{2} x_{N}\right) \end{array}\right]$

这里留一个思考题（结尾公布答案）：

这里我们所说的都是黑白组成额灰度图像，那么对于彩色的RGB格式图像来说，我们又该如何表达呢？

二 . 框架实现

在实现我们的映射之后，我们怎样才能将这些像素数据进行批量的操作？要解决这个问题我们要先弄明白最终的目标是什么，还是需要确定方向：

在深度学习中，MNIST 手写数据集的识别问题是一个非常著名的分类问题，并且它是60000张灰度图片，完全吻合我们这篇论文的需求!

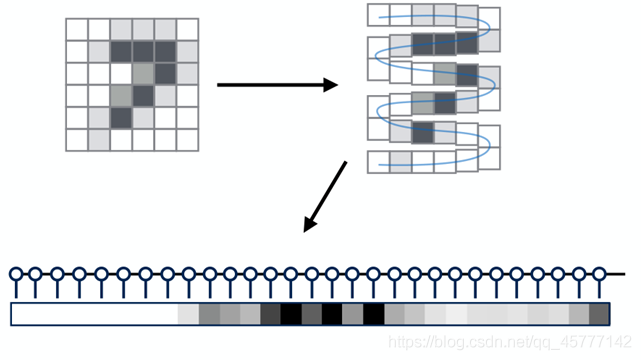这张图片就是MNIST图片中像素大小为6x6，图案为数字7的一张手写图片，我们需要通过一系列操作，使其最后的返回结果为 ：“7”。说白了，就是算法要识别出这个图片的内容！

同时，这张图片也为我们非常直观的展示了下一步的流程，将像素数据排成一排并组成MPS，对于不同的图片像素，不同系数的量子态排列之后的相对位置也是不同的，在经过训练好的trian 模型之后，返回的应当就是我们需要的预测标签！那么重点就来了，这个拟合到返回预测标签的过程是我值得研究的！

还是看图说话：

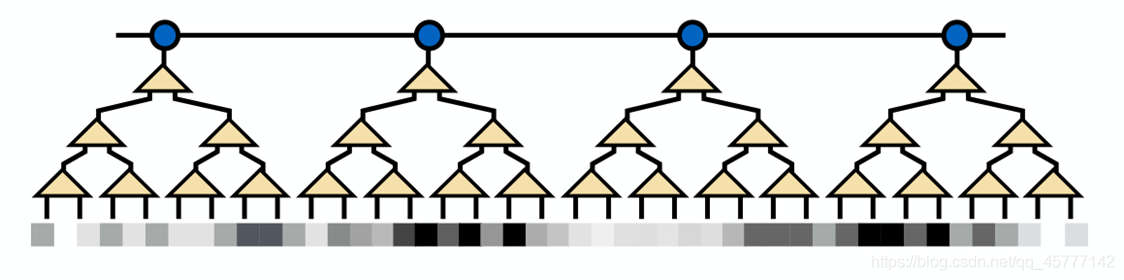
这里运用到的主要就是粗粒化的思想，他也是张量网络中的核心思想，其目的是不断的丢弃尺度较小的信息从而是全局的重要信息显露出来，让原先的数据呈现出越来越宏观的趋势！

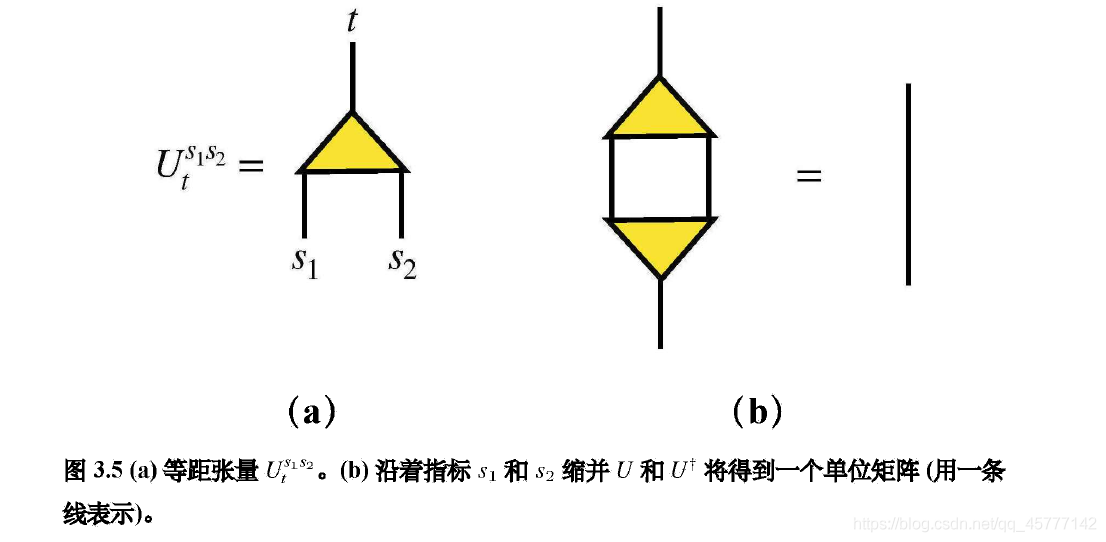
在看懂这个图之前，先来看看啥是等距张量！这个非常简单的一个定义，一图足以：
当我们把所有的输入元素数据对应叠加态的等距张量求出来之后，我们就得到了一个等距变换层（也就是上上个图中的一排三角形，注意这里就不是张量了哦），此等距层就可以用来粗化每个训练集的特征向量 $\Phi (x_{j})$ (其实这里还有一个创建协方差矩阵进行对角化的过程，这里不需要深究 ，理解意思即可)，通过不断的迭代这一过程，不断的丢掉特征不明显的信息，我们就得到了一个树状的张量网络！这个树状网络通过不断的投影可以极大的压缩特征向量的表示维度，同时也保留了其主要成分！

最终顶层的蓝色圆圈代表的就是预测好的标签！

三 . 量子电路

我们将要考虑的树形张量网络和MPS总是可以由量子电路精确地实现，通常，我们对应于张量网络的量子电路是经过精心设计的，以使它们能够有效地用经典计算机进行准备和操作。随着键维的增加，树和MPS张量逐渐捕捉到更大范围的状态，最终形成完整的希尔伯特空间！

我们将要研究的电路包含许多一开始就没有确定的参数（模型参数），只有电路的几何结构是固定的，而决定么正运算的参数必须针对特定的机器学习进行优化！下面看图，别懵：

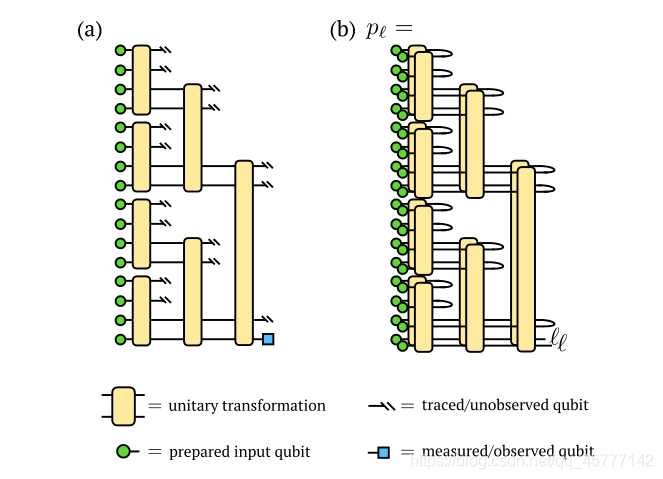此图与前面的张量树是等价的！

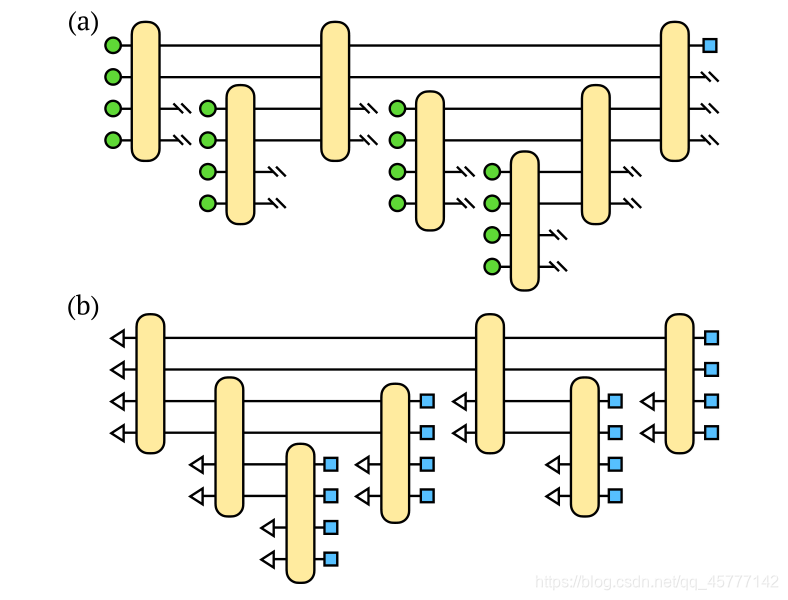
先看左边的图，最左边一共有16个绿色的小圆圈，他们代表的就是16个像素的图片，也就是每个小圆圈代表的是由量子叠加态组成的一个已经准备好的像素数据的输入，显然，每四个为一组进行酉变换，对于输入的像素数据不同，具体的每一个酉变换也会根据其产生的触角而做出相应的改变，之后就用到了前面的粗粒化思想，丢弃掉部分特征信息（就是图中的双斜杠，进行求迹，也可以不做处理），这里我们四取二，如图所示，继续迭代操作，最终得到我们可测量观测的量子比特，对应的就是最终的输出标签！

由于酉矩阵的逆矩阵和它的共轭转置是相同的，所以，上面右图就是复制后的共轭转置与原来的电路结合，原本求迹的部分就缩并成了一个单位矩阵，这是对于多层图像的处理，可以看到，最后的输入直接变成了两个标签值 $l$ 。

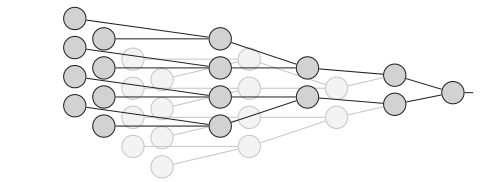
这张图片就是刚才量子电路图的宏观表达，四个像素为一组，分成四组，最右边的也就是输出的标签值！

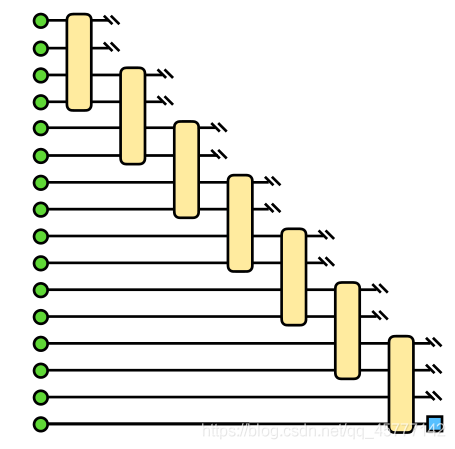这个它的另一种量子电路图，即MPS对应 的二叉树的最大不平衡树，和前面的两张图片的本质是一模一样，唯一不同的就是这个电路是对输入的像素数据挨个处理，而前面的有种随机处理的感觉！

四 . 算法

我们先来看一张图片并总结不同的地方！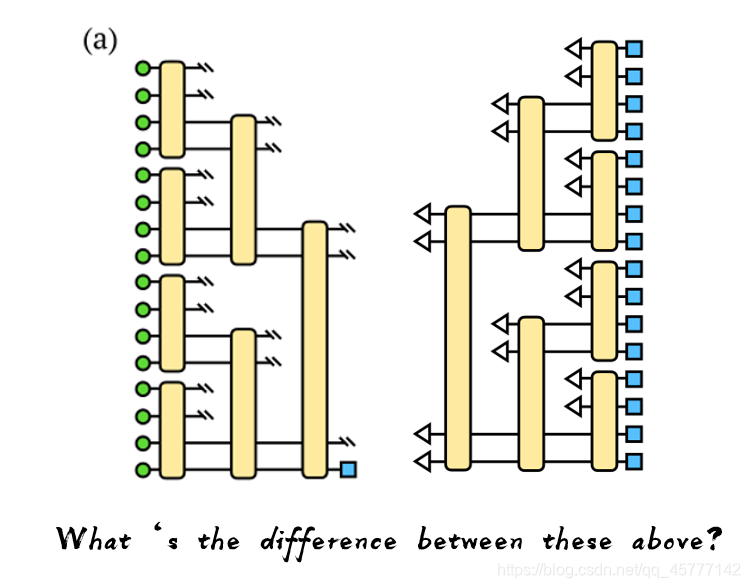

1. 首先映入眼帘的就是左边的一列表示像素数据的绿色小圆圈 ，到了右边图中就变成三角形了；我们知道对于绿色圆圈来说，它代表的一个量子叠加态，而三角形论文里面给出的是 [0,1] 这样的一个基态，是一个确定的状态！
2. 其次，我们显然发现这两张图片是轴对称的，说明他们的线路运行是相反的！
3. 最后，原本结尾处只有一个蓝色的可观测量子比特，到了右图中，也没有丢弃信息了，都返回了可观测的标签值了

目标决定过程，过程控制方法！产生这些不同的根本原因还是算法的不同！

上面的左右两个量子电路分别对应的就是 判别算法 和 生成算法 ！

对于判别算法来说，会将原本的数据集二八分成train 和 test 数据集，用train数据集拟合好模型之后，代入test数据进行预测，最后返回出来的一般情况下只有一个预测标签，而对于生成算法而言，我们会提前准备好一个图片或者其中的特征，代入每一个标签分类器中 进行对比 ！所以它返回出来的是所有标签的 预测概率，我们只需要选其中的最大概率标签值即可！

这里有个非常好的例子帮助大家理解：

判别式模型举例：要确定一个羊是山羊还是绵羊,用判别模型的方法是从历史数据中学习到模型然后通过提取这只羊的特征来预测出这只羊是山羊的概率,是绵羊的概率。

生成式模型举例：利用生成模型是根据山羊的特征首先学习出一个山羊的模型,然后根据绵羊的特征学习出一个绵羊的模型,然后从这只羊中提取特征,放到山羊模型中看概率是多少,在放到绵羊模型中看概率是多少,哪个概率大就是哪个！

所以，从这个角度来说，就解释了为啥会出现这三个不同！

五 . 优化

这篇论文的前半部分告诉我们基于监督学习的张量网络在图像处理上面的一些原理，包括算法之类的核心点，论文的后半部分主要讲的就是优化的过程，先是优化损失函数 ，让其变得更准确，再是优化量子电路，使其更高效，二者结合，会使图像处理既准确又高效！

1. 损失函数

我们的最终目标是选择电路的参数，这样我们就可以通过少量运行电路来更高效地为新数据分配正确的标签，所以我们不得不引入损失函数。这里的损失函数和我们通常在机器学习中使用的MSE 有些不一样，我们下面具体的来看一下：

先注明这些符号的含义： $\boldsymbol{\Lambda}$ 代表的是电路模型的参数组成的向量；x 是训练数据集的元素； $p_{\ell}(\mathbf{\Lambda}, \mathbf{x})$ 是对于给定输入的 x ，输出标签为 $\ell$ 的概率； $\ell_{x}$ 代表的是输入 x 后应当返回的正确标签 。

我们首先定义当预测结果与真实结果不相同时，我们选取错误率最大的并定义如下（因为错误率越高，越容易观测和纠正）：

$p_{\text {largest false }}(\boldsymbol{\Lambda}, \mathbf{x})=\max _{\ell \neq \ell_{\mathbf{x}}}\left[p_{\ell}(\mathbf{\Lambda}, \mathbf{x})\right]$

紧接着我们就可以定义单个输入像素数据集的损失函数：
$L(\boldsymbol{\Lambda}, \mathbf{x})=\max \left(p_{\text {largest false }}(\boldsymbol{\Lambda}, \mathbf{x})-p_{\ell_{x}}(\boldsymbol{\Lambda}, \mathbf{x})+\lambda, 0\right)^{\eta}$
这里我们需要引入超参数 $\lambda$ 和 $\eta$ ，这也是机器学习中我们经常使用的，由于在真正的去建立模型拟合的时候，对于返回出来的概率值多多少少还是有些偏差，这里的 $\lambda$ 就给予了模型一定的容错性，在一定的范围内，我们还能使得 $L(\boldsymbol{\Lambda}, \mathbf{x})$ 返回的是正值！除此之外，对于真实值与预测值的差值，不同的大小我们会给予不同的权重，这也就是 $\eta$ 的作用！

那么对于所有的训练图片，我们求整体的损失函数，再进行归一化处理就得到如下：
$L(\boldsymbol{\Lambda})=\frac{1}{| \text { data }|} \sum_{\mathbf{x} \in \text { data }} L(\boldsymbol{\Lambda}, \mathbf{x})$

当然，我们感兴趣的是训练我们的电路很好地推广到未观察到的输入，因此，不需要像上面那样优化整个数据分布，而是在训练数据的子集上优化损失函数，并与保持不变的测试数据集进行比较。

此外，由于典型机器学习问题的训练集的大小非常大(在MNIST数据集的情况下为60000个示例)，因此计算每个优化步骤中所有训练数据的损失是不切实际的。取而代之的是，我们遵循机器学习的标准方法，并在每次迭代中随机选择一小批训练示例：
$\tilde{L}(\boldsymbol{\Lambda})=\frac{1}{\mid \operatorname{mini}-\text { batch } \mid} \sum_{\mathbf{x} \in \operatorname{mini}-\text { batch }} L(\mathbf{\Lambda}, \mathbf{x})$

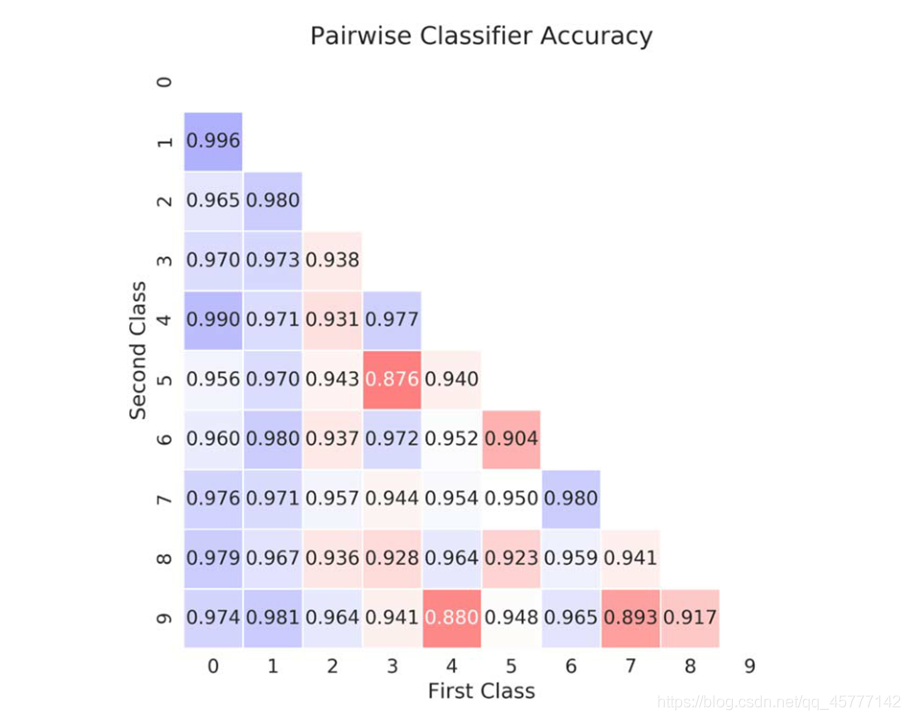这是对于之前的MNIST手写数据集按照上述相关方法操作之后 得到的一个手写数据准确率预测的分类器，上面都是模型预测的准确率！

2. 线路优化

在大致的看完损失函数之后，准确率提升的部分算是成功实现了，那么对于效率的优化问题，我们需要改进原先的电路结构；根据前面说的我们 引入多少个 像素数据 就需要引入多少个新的量子态 但是毫无疑问 量子态引入的越多 计算带来的难度也就是越大 耗费的时间也就越多 ！

再回到我们之前介绍电路的时候，在张量树的部分用到了粗粒化的思想，所以对于我们输入的所有量子比特，必然要舍弃到一大部分，那么对于这些损失的量子比特，能不能采用特定的方法对他们进行重复利用 呢？

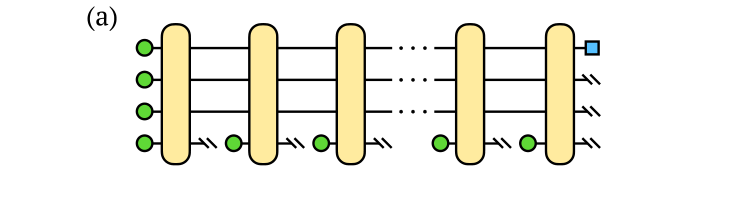
仔细看这幅图，在原本求迹或者舍弃的量子态后面，我们又继续使用了两个量子态代表的像素继续代入下一步的酉变换！

论文再现: 这里告诉了我们对于之前的量子线路中，单单的量子状态准备和 幺正运算 依然需要 N 个量子态（比特），但是 增加的重整和测量的相关操作之后，我们可以将原本需要的 量子比特数目以对数型趋势缩减！这里的 $V$ 就是连接子树与子树之间的 “量子线” ！

那么对于刚才那个图，V=2，原本需要我们引入16个新的量子比特，但是 这里只需要 8个，如下图所示：

对于原本的量子态，重整之后可以重复利用，较好的缓解了多量子态引入之后产生的误差，纠错等一系列问题，提升了运算效率！

那么对于数量巨多的像素图片而言，我们最少需要新引入多少个量子比特呢？这就取决我们每次保留的量子态（量子线）了！

这个图片明确的告诉我们，先引入与量子线数目相等的qubits ，在引入的qubit 我们反复测量，反复重整，这就有点无赖的感觉了，这也就是量子计算机的 变态之处！

最后这篇论文还在量子线路子树的左右两个节点引入了噪音，但是需要一些较强的物理知识，计科狗表示 tmd 直接劝退，等我研究好了 再来补充！

好的，这篇论文的大概就是这些 ，希望大佬们多多指点！