论文阅读：DeepWalk Online Learning of Social Representations

论文大纲

• Introduction （介绍了论文的任务，概括了论文的工作）
• Problem Definition（定义了
• Learning Social Representation
• Method
• Experimental Design & Experiments
• Related Work
• Conclusinos

问题定义

在社交网路中，结点的表示通常是稀疏的，这给存储和计算都带来了不便。给定社交网络中，学习网络中每个结点的隐表示（latent representation）。简单来说，就是用一个稠密的向量来表示网络中的结点。这样的向量应该具备以下这四个特点：

• Adaptability: 学习到的representation应该能够适应网络局部的变化，当网络某个局部变化时，能够local updating，不需要对整个网络重新计算；
• Community aware: 相似的结点（结构相似、在网络中的位置相似等）的表征（representation）应该距离很近；
• Low dimensional
• Continuous: 表示结点的向量应该是实值向量。

贡献

• 第一次将深度学习的方法引入网络分析中（但是论文看下来，感觉里面就skip gram中的三层网络和梯度下降方法能和DL扯上点关系），将学习到的结点表征作为统计模型的输入；
• 在网路的多分类任务（及对每个结点进行多分类）中验证了Deepwalk得到的结点向量的有效性，使用更少的数据（原来的40%）取得了更好的效果；
• 实现了并行计算结点表征的方法（主要是Random walk可以并行）；

使用Deepwalk学习结点表征

给定一个网络G，为了用一个实值向量表示网路中的一个结点，该从哪些方面入手呢？
论文中将语言建模的技术用来求结点的表征。主要借鉴的是word2vec [2]中的skip gram。

思路大概是这样的

首先，随机初始化每个结点的表征，令所有结点的表征为 $\phi$ 。
通过RandomWalk，以G中的结点v为RandomWalk的起点来产生一个结点序列，这样就作为一个样本W_v。将这个样本输入到skip gram里，通过最大化RandomWalk中结点的共现概率来更新 $\phi(v)$。把所有的样本都跑完之后，得到的 $\phi$就是我们想要的G的每个结点的表征了。

detail0：为什么可以将语言模型中的技术用在结点表征中？

这都源于power law—幂律分布。

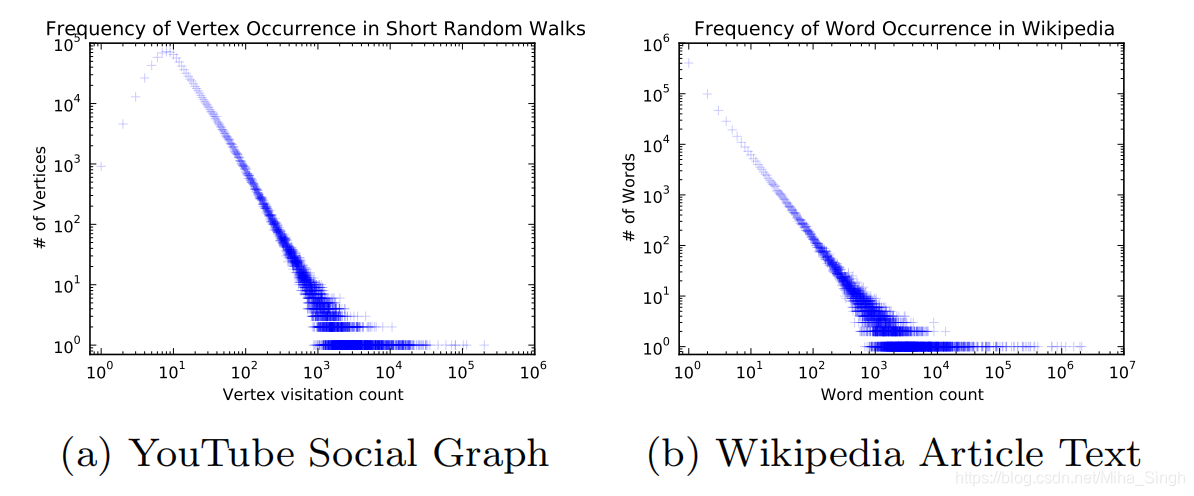
文本数据集中单词频率的分布遵循幂律分布，由随机游走序列组成的数据集中，结点出现的频率也遵循幂律分布。上图即论文中的一幅图，分别代表YouTube社交网络中随机游走后结点的频率分布和Wikipedia中单词的频率分布。这一个规律是论文中将语言模型的技术应用于结点表征的一个原因。

detail1：为什么最大化结点的共现率可以用来更新 $\phi$?

这还要从语言模型[3]讲起，language model 的一个目标就是估计一个句子的概率，已知一个句子:
当给定 $w_{0}w_{1}...w_{n-1}$时，最大化下一个词为 $w_{n}$的概率，即
$maximize Pr(w_{n} | w_{0}w_{1}...w_{n-1})$类似的，为了捕捉住结点在网络中的信息，我们希望
$Pr(v_{n} | v_{0}v_{1}...v_{n-1})$（其中v_{0}v_{1}…v_{n}为随机游走序列）能够最大化（尽可能地符合真实数据）。
但是我们并不是单单为了求一个结点序列的概率，我们的目标是为了求 G中每个结点的表征 。还记得上文中我们提到的 $\phi$吗？上文中是把它当作包含所有结点表征的一个矩阵，但我们也可以把它当作一个映射，输入结点，返回该结点的表征，即 $\phi:v\in V \mapsto \mathbb{R}^{|V| \times d}$。那么上个公式就成了：
$Pr(v_{n} | \phi(v_{0})\phi(v_{1})...\phi(v_{n-1})$但是随着随机游走长度的增加，计算这个值会变得很耗时。
在[2] 中提出了CBOW和SkipGram模型，都是用来生成词向量的方法，但是CBOW是通过上下文预测中心词的方法来学习词向量，SkipGram是通过中心词来预测上下文的方法，如图所示：

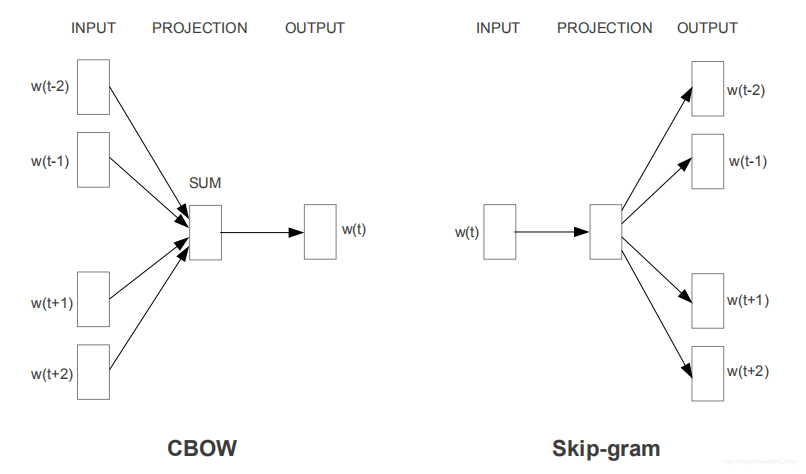
论文中不去求
$Pr(v_{n} | \phi(v_{0})\phi(v_{1})...\phi(v_{n-1})$
转而去求
$Pr({v_{i-w},...v_{i-1},v_{i+1},...,v_{i+w} } | \phi(v_{i}) )$
其中w是skip-gram算法中的窗口的大小。
论文中引入了一个假设：结点之间是相互独立的。引入这个假设有两个原因：

• 假设结点之间是相互独立的更好的捕捉了随机游走中结点间的“临近(nearness)”；
• 加速计算；
  根据这个假设就有：
  $Pr({v_{i-w},...v_{i-1},v_{i+1},...,v_{i+w} } | \phi(v_{i}) ) = \prod_{j=i-w,j\neq i}^{i+w}Pr(v_{j} | \phi(v_{i}))$
  最大化这个值就是我们的目标。

detail2：Hierarchical tree？

既然我们已经获得了要优化的目标，那就可以直接去算了吗？No！No！No！
对于每一个结点对都去计算 $Pr(v_{j} | \phi(v_{i}))$是不可行的。论文中引入了Hierarchical Softmax来降低计算难度。首先，以每个结点在所有随机游走序列中出现的频率构建Huffman tree。

在论文中并没有对Hierarchical Softmax进行过多的介绍，但是在word2vec相关的资料中有较多讲解。
在计算 $Pr(v_{j} | \phi(v_{i}))$时，将其转化为在构建好的Huffman tree中，从根节点到叶子节点的概率。例如计算 $Pr(v_{3} | \phi(v_{i}))$时，从根节点到叶子结点 $v_{3}$所经过的结点为 $b_{0}b_{1}...b_{k}, 其中b_{0}为根节点，b_{k}=v_{3}，除b_{k}为Huffman tree 内部结点$，则 $Pr(v_{3} | \phi(v_{i})) = \prod_{j=1}^{k}Pr(b_{j} | \phi(v_{i}))$那么问题来了， $Pr(b_{j} | \phi(v_{i}))$该怎么算呢？
论文中是这样介绍的：给每个内部结点赋予一个而分类器，这个分类器决定选择该结点的左右子结点的概率。所以从根节点开始到叶子结点，相当于从根结点的走到叶子结点，不断进行向左、向右的选择。所以 $Pr(b_{j} | \phi(v_{i}))$ 的计算方法为： $b_{j}$的父结点 $b_{l}$选择方向时选择 $b_{j}$的概率。

Deepwalk 伪代码

从算法的伪代码可以看出，所有结点的表征 $\phi$从均匀分布中进行采样，然后构建Huffman tree，伪代码中Huffman tree的构建实在randomwalk之前，但是在论文中提到了进一步加速算法的方法就是依据随机游走的数据集构建Huffman tree。通过随机游走获得随机游走序列的数据集后，就通过skip-gram和SGD方法更新 $\phi$。
Deepwalk的源码：deepwalk
关于deepwalk源码的一个问题：

在Windows10平台运行代码时，有一个bug：AttributeError: ‘NoneType’ object has no attribute ‘nodes’。
原因是因为Deepwalk中使用了多进程，在python的多进程间默认是不共享变量的。具体的解决方法可以看Deepwalk的GitHub中的 issues 54。

参考文献

[1] Perozzi, Bryan, et al. “DeepWalk: Online Learning of Social Representations.” Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2014, pp. 701–710.
[2] Mikolov, Tomas, et al. “Efficient Estimation of Word Representations in Vector Space.” ICLR (Workshop Poster), 2013.
[3] Bengio, Yoshua, et al. “A Neural Probabilistic Language Model.” Journal of Machine Learning Research, vol. 3, no. 6, 2003, pp. 1137–1155.