CF825F String Compression

一、题目

点此看题

二、解法

显然有一个简单 $dp$， $dp[i]$表示前 $i$个字符压缩的最小长度，转移需要找出一段后缀的最小周期。

如何找最小周期呢？有一个结论：最小周期=长度-最长公共前缀后缀（ $kmp$），证明请看下图：

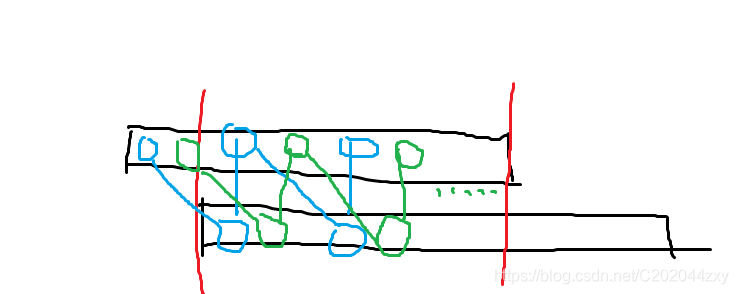
其中红色部分就是最长公共前缀后缀，上图表示了同一个字符串的移位，连线表示相等，周期的形成显然…

那么跑一个 $kmp$转移就很方便了，但是要注意上图算出来的周期不一定整除长度，与我们需要的题目中的周期有一些出入，但这种情况出现的时候只能取整段了（其他周期是最小周期的整数倍），时间复杂度 $O(n^2)$

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define inf 0x3f3f3f3f
const int M = 55;
int read()
{int x=0,flag=1;char c;while((c=getchar())<'0' || c>'9') if(c=='-') flag=-1;while(c>='0' && c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();return x*flag;
}
int n,m,K,a[M],b[M],c[M];
int ok1[M][M][M],ok2[M][M][M],dp[M][M];
char s[M],t[M],str[10];
int main()
{scanf("%s%s",s+1,t+1);n=strlen(s+1);m=strlen(t+1);K=read();for(int i=1;i<=K;i++){scanf("%s",str);a[i]=str[0]-'a';b[i]=str[3]-'a';c[i]=str[4]-'a'; }for(int i=1;i<=n;i++)ok1[i][i][s[i]-'a']=1;for(int i=1;i<=m;i++)ok2[i][i][t[i]-'a']=1;for(int i=n;i>=1;i--)for(int j=i+1;j<=n;j++)for(int k=i;k<j;k++)for(int w=1;w<=K;w++)if(ok1[i][k][b[w]] && ok1[k+1][j][c[w]])ok1[i][j][a[w]]=1;for(int i=m;i>=1;i--)for(int j=i+1;j<=m;j++)for(int k=i;k<j;k++)for(int w=1;w<=K;w++)if(ok2[i][k][b[w]] && ok2[k+1][j][c[w]])ok2[i][j][a[w]]=1;memset(dp,0x3f,sizeof dp);dp[0][0]=0;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)for(int k=1;k<=i;k++)for(int l=1;l<=j;l++)for(int w=0;w<26;w++)if(ok1[k][i][w] && ok2[l][j][w])dp[i][j]=min(dp[i][j],dp[k-1][l-1]+1);if(dp[n][m]==inf) puts("-1");else printf("%d\n",dp[n][m]);
}