《高等数学》笔记——第十二章：无穷级数

第十二章：无穷级数

常数项级数的概念和性质

一、概念

1. 级数定义：

给定数列 $\{u_n\}$ ，由数列构成的表达式： $u_1+u_2+u_3+...+u_n+...$称为常数项级数 ，简称为级数，记做 $\sum\limits_{n=1}^{∞}u_n$

2. 有限和式： $u_1+u_2+...+u_n$称为 $\sum\limits_{n=1}^{∞}u_n$的前n项部分和

   无穷数列： $s_1,s_2,...,s_n$称为 $\sum\limits_{n=1}^{∞}u_n$的部分和数列

3. 收敛和发散的定义：

   如果 $\sum\limits_{n=1}^{∞}u_n$的部分和数列 $\{s_n\}$有极限，那么级数收敛，反之，极限不存在，那么级数发散

4. 余项的定义

   级数收敛时，称 $r_n=s-s_n=u_{n+1}+u_{n+2}+...+$为级数的余项

   且有 $\lim_{n\rightarrow\infty}r_n=0$

二、常用的级数的敛散性

1. 等比级数

   $|q|<1$：级数收敛

   $|q|≥1$ : 级数发散

2. 调和级数

   调和级数虽然一般项趋近于0，但是级数发散，可见，一般项趋于零不能成为判定级数发散的标准。

3. p级数

   形如： $1+\frac{1}{2^p}+\frac{1}{3^p}+...+\frac{1}{n^p}+...$

   $p>1$：收敛

   $p≤1$：发散

三、级数的性质

1. 若级数 $\{u_n\}$收敛于s,那么s= $\sum\limits_{n=1}^{\infty}u_n$，则各项都乘以常数c，得到的级数 $\sum\limits_{n=1}^{\infty}cu_n$ ,也收敛，其和为 $cs$

2. 设有两个收敛级数 $s=\sum\limits_{n=1}^{\infty}u_n$和 $\sigma=\sum\limits_{n=1}^{\infty}v_n$ ，则级数 $\sum\limits_{n=1}^{\infty}(u_n±v_n)$也收敛，收敛于 $s±\sigma$

   推论：收敛+收敛=收敛

   ? 收敛+发散=发散

   ? 发散+发散=不一定

3. 在级数前面加上或者去掉有限项，不改变原级数的敛散性

4. 收敛级数加上括弧后的级数仍收敛于原级数。

   推论：如果加上括弧后发散，那么原级数一定发散

   注意：收敛级数去括号后的级数未必收敛

5. 如果级数收敛，那么一般项一定极限为无穷小，即 $\lim_{n\rightarrow\infty}u_n=0$ （必要条件）

   推论：级数的一般项不趋于0，则级数一定发散

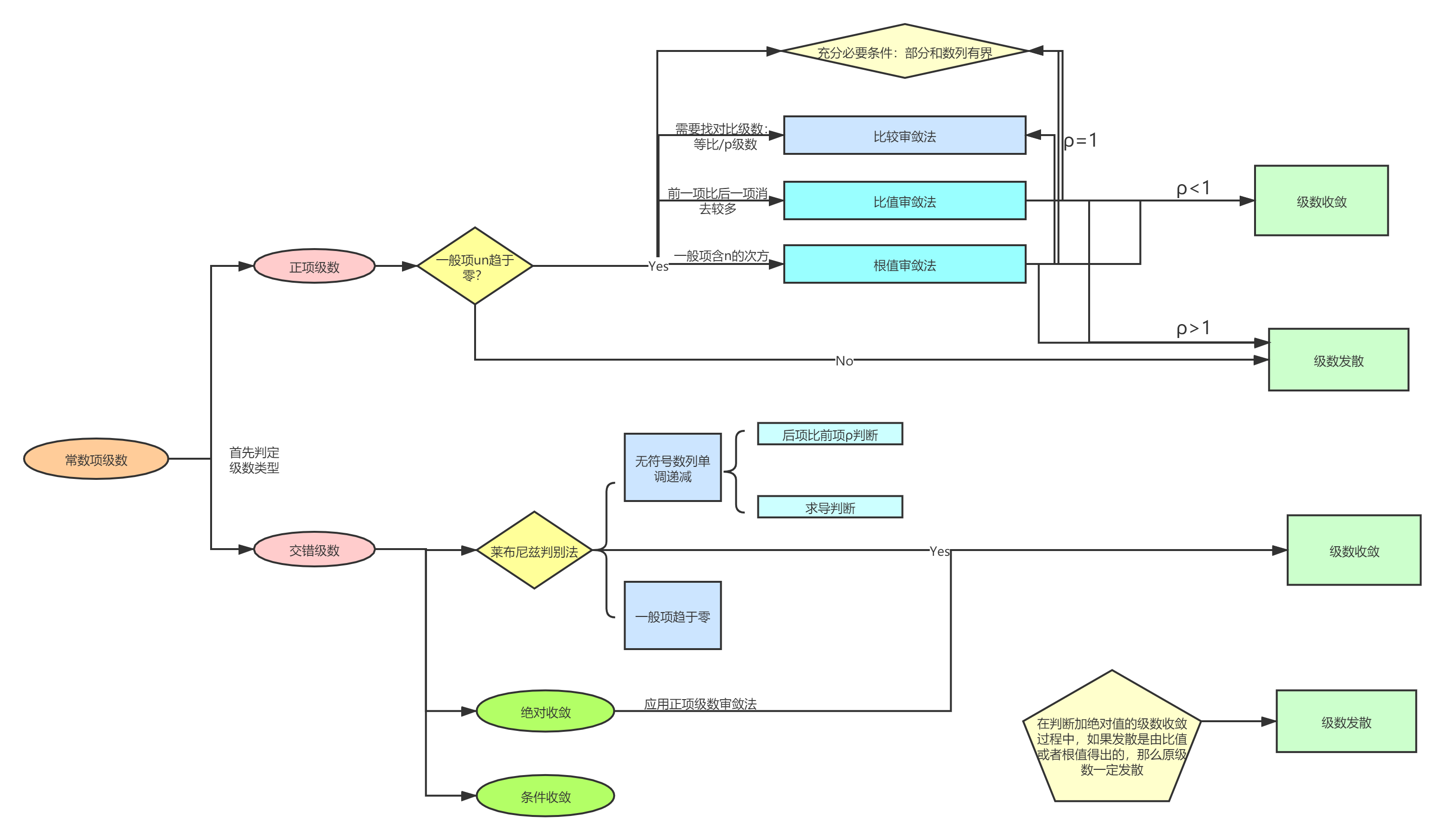
常数项级数审敛法

一、正项级数及其审敛法

1. 正项级数的概念：每一项都大于等于0

2. 正项级数的审敛法

   ①收敛的充要条件：部分和数列 $\{s_n\}$有界

   ②（比较审敛法）：

   设 $\sum\limits_{n=1}^{\infty}u_n$和 $\sum\limits_{n=1}^{\infty}v_n$ 都是正项级数，且 $u_n≤v_n（n=1,2,...）$

   大的收敛，小的一定收敛：若级数 $\sum\limits_{n=1}^{\infty}v_n$收敛，则级数 $\sum\limits_{n=1}^{\infty}u_n$收敛

   小的发散，大的一定发散：若级数 $\sum\limits_{n=1}^{\infty}u_n$发散，则级数 $\sum\limits_{n=1}^{\infty}v_n$发散

   推论：如果 $\sum\limits_{n=1}^{\infty}u_n$和 $\sum\limits_{n=1}^{\infty}v_n$ 都是正项级数

   a. 如果 $\sum\limits_{n=1}^{\infty}v_n$ 收敛，且存在正整数N，使当n≥N时有 $u_n≤kv_n(k>0)$成立，那么级数 $\sum\limits_{n=1}^{\infty}u_n$收敛

   b. 如果 $\sum\limits_{n=1}^{\infty}v_n$ 发散，且存在正整数N，使当n≥N时有 $u_n≥kv_n(k>0)$成立，那么级数 $\sum\limits_{n=1}^{\infty}u_n$发散

3. 比较审敛法的极限形式

   设有两个正项级数： $\sum\limits_{n=1}^{\infty}u_n$和 $\sum\limits_{n=1}^{\infty}v_n$，且满足 $\lim_{n\rightarrow\infty}\frac{u_n}{v_n}=l$

   (1)当 $0<l<\infty$时： $\sum\limits_{n=1}^{\infty}u_n$和 $\sum\limits_{n=1}^{\infty}v_n$同敛散性

   (2)当 $l=0$且 $\sum\limits_{n=1}^{\infty}v_n$收敛时， $\sum\limits_{n=1}^{\infty}u_n$也收敛

   (3)当 $l=\infty$且 $\sum\limits_{n=1}^{\infty}v_n$发散时， $\sum\limits_{n=1}^{\infty}u_n$也发散

4. 比值审敛法（达朗贝尔判别法）

   设 $\sum\limits_{n=1}^{\infty}u_n$ 为正项级数

   如果 $lim_{n\rightarrow\infty}\frac{u_{n+1}}{u_n}=\rho$

   (1) $\rho<1$：级数收敛

   (2) $\rho>1$：级数发散

   (3) $\rho=1$：不确定

   优点：不必找参考级数

   注意：比值审敛法是必要的，而不是充分的：

   不能通过 $\sum\limits_{n=1}^{\infty}u_n$ 收敛 $\longrightarrow\lim_{n\rightarrow\infty}\frac{u_{n+1}}{u_n}=\rho<1$

5. 根值审敛法（柯西判别法）

   设 $\sum\limits_{n=1}^{\infty}u_n$ 为正项级数

   如果 $lim_{n\rightarrow\infty}\sqrt[n]{u_n}=\rho$

   (1) $\rho<1$：级数收敛

   (2) $\rho>1$：级数发散

   (3) $\rho=1$：不确定

二、交错级数及其审敛法

1. 交错级数的概念：各项正负交错，可以写成下面的形式：

   $u_1-u_2+u_3-u_4+...$

2. (莱布尼茨定理)如果交错级数 $\sum\limits_{n=1}^\infty(-1)^{n-1}u_n$满足条件：

   (1) $u_n≥u_{n+1}(n=1,2,3,...);$或 $u_n≥u_{n+1}(n≥N)$-----------------------------------不看符号单调递减

   (2) $lim_{n\rightarrow\infty}u_n=0,$-----------------------------------------------------------------------------------不看符号一般项趋于零

   那么级数收敛，且其和 $s≤u_1$，其余项 $r_n$的绝对值 $|r_n|≤u_{n+1}$

   注意：对于条件(1)中的数列单调性的判断常用的方法如下：

   ① $\frac{u_{n+1}}{u_n}=\rho$，根据 $\rho$与1的大小判断单调性

   ②求导（容易忘记！！！）

3. 绝对收敛与条件收敛

   定义1：对于任意项级数 $\sum\limits_{n=1}^{\infty}u_n$，若 $\sum\limits_{n=1}^{\infty}|u_n|$收敛，那么称原级数绝对收敛

   （注意：一般来说加绝对值之后发散，原级数敛散性仍需重新判断，但是如果用的比值或者根值审敛法判定的发散，那么原级数一定发散）

   定义2：若原级数收敛，加上绝对值之后发散，那么称原级数 $\sum\limits_{n=1}^{\infty}u_n$条件收敛

   定理：绝对收敛的级数一定收敛：通过加绝对值后收敛判断原级数一定收敛

常数项级数总结