20200719005916
2020牛客暑期多校03 D - Points Construction Problem
题意
无限大的二维平面上,所有整数点(横纵坐标都是整数的点)初始都为白色。给定 ,要求将其中 个点染成黑色,使得满足以下条件的点对 恰有 组:
- 两点颜色不同;
- 两点相邻,即 ;
只需找出任意一种染黑方案并输出 Yes 以及所选
个染黑点的坐标
,或者输出 No 表示答案不存在。
。
题解
如下图,将每个整数点视为一块正方形,相邻整数点对应的正方形相接,正方形边长为 ,(答案中)黑点对应正方形染成深色(蓝)、白点对应正方形染成浅色(黄)。那么, 个染黑的整数点就对应 个深色正方形、 组题述的点对就对应 条深浅相交处的边,再进一步说,图中深色部分面积为 、周长为 。

因此问题转化为,在无限大的浅色网格平面中染深一些正方形,使深色部分面积为 、周长为 。
为奇数时答案不存在。因为从任意一行从左向右穿过,都会反复进入、离开深色块,从任意一列从上向下穿过同理,因此周长 必为偶数。
下面我们来研究,给定周长 ,我们最多、最少可以染多大面积 。
首先要认识到,对于一个
- 连通的、
- 横坐标跨度为 的(即,被染色的正方形当中的最小横坐标 与最大横坐标 之差 )、
- 纵坐标跨度为 的(定义同理)
- “凸”多边形,
我们可以使其膨胀或收缩而改变面积,但只要变化过程中其保持上述四性质不变,其周长不会变!这是因为,膨胀和收缩的操作可以视为周长边发生平移。如下图( ),左侧经过膨胀变为右侧而周长不变:

换句话说,此时周长只与横坐标、纵坐标的跨度有关,或者说只与染色块撑起的矩形区域有关。
上述 “凸” 多边形打了双引号,并不是指通常意义上的凸多边形,只要不存在某个完全凹进去的、三面环绕的 “港湾” 区域就可。如果收缩过程中出现了上述港湾块,周长就会多出至少两条边,如下图:
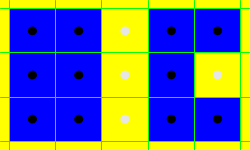
**给定周长,最少可以染多大面积?**经过极限的收缩,如果要撑起一个横坐标跨度为 、纵坐标跨度为 的区域(周长为 ),染色面积最小可降至 ,或者说,最少只需染 个正方形即可撑起一个横坐标跨度为 、纵坐标跨度为 的区域。方案如下图( ):尽可能全部摆在对角线处,使每个染色正方形都能同时对横纵坐标的跨度增加做出贡献。
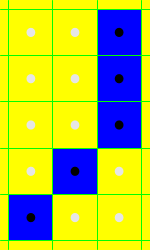
然而题目只给定了周长 ,并未指定 ,那么为了使 最小,我们应取 。因此,周长为 时, 最小可取 。
**给定周长,最多可以染多大面积?**经过极限的膨胀,一个横坐标跨度为 、纵坐标跨度为 的区域(周长为 ),染色面积显然最大为 。然而题目只给定了周长 ,并未指定 ,那么为了使 最大,我们仍应取 。因此,周长为 时, 最大可取 。
刚才的一系列讨论是基于【答案只在一个 “区域” 内染色】的假设的。
如果可以撑起多个区域来染色,给定周长 ,最少可以染多大面积?由于 个正方形总共只有 条边,因此 即 ,可见只撑起一个区域时 最小取得 已是最优方案。
如果可以撑起多个区域来染色,给定周长 ,最多可以染多大面积?我们考虑先把多个区域内所有正方形全部染色。这时,将各区域平移使多个区域融合成一个区域,会发现有一些周长边在融合时消失,说明当前的染色面积可以由更少的周长在一个撑起区域内实现,既然如此,那么当前周长值就应该能够染更多面积,因此,撑起多个区域的方案不会是最优的。
接下来就是染色方案了。我们永远将给定的周长 撑起一个跨度为 的区域,先在对角线以及 多出的长条部分上染色、确保先用 个正方形把区域撑起来,再不断在当前已染区域的相邻斜线上染色,直到染够 个正方形,如下图左侧。注意,不可横着或竖着染色,否则不满足 “凸” 多边形的要求,如下图右侧。

AC代码
#include<cstdio>void solve(int n , int m){if(m%2==1){printf("No\n");return; //continue;}int x = m/4;int y = m/2 - x;if(n<y || n>x*y){printf("No\n");return; //continue;}printf("Yes\n");for(int i=1 ; i<=x && n>0 ; ++i) {printf("%d %d\n" , i , i);--n;}if(x<y && n>0) {printf("%d %d\n" , x , y);--n;}// for(int i=1 ; i<=x && n>0 ; ++i){
// for(int j=1 ; j<=y && n>0 ; ++j){
// if(i==j) continue;
// printf("%d %d\n" , i , j);
// --n;
// }
// }for(int d=1 ; d<=x && n>0 ; ++d){for(int i=1 ; i<=x && n>0 ; ++i){if(i+d>x) break;printf("%d %d\n" , i+d , i);--n;}}for(int d=1 ; d<=y && n>0 ; ++d){for(int i=1 ; i<=x && n>0 ; ++i){if(i+d>y) break;if(i==x && i+d==y) continue;printf("%d %d\n" , i , i+d);--n;}}
}int main(){// for(int m=1 ; m<=50 ; ++m){
// for(int n=1 ; n<=10 ; ++n){
// printf("\n\nn=%d , m=%d:\n" , n , m);
// solve(n,m);
// }
// }int t;scanf("%d" , &t); //printf("%d\n" , t);while(t--){int n,m;scanf("%d%d" , &n , &m); //printf("%d %d\n" , n , m);solve(n,m);}return 0;
}