目录
insight
Method
Template
Revisiting Simple Neurons
Aggregated Transformations
Model Capacity
Experiments
Experiments on ImageNet-1K
Cardinality vs. Width
Increasing Cardinality vs. Deeper/Wider
Residual connections
Comparisons with state-of-the-art results
Experiments on ImageNet-5K
Experiments on CIFAR
Experiments on COCO object detection
这是一篇发表在2017CVPR上的论文,介绍了ResNet网络的升级版:ResNeXt。
本文提出了一种简单、高度模块化的图像分类网络结构ResNeXt(暗示着下一个维度),通过重复一种构造块来构建,这种构造块聚合具有相同拓扑的一组转换(这个策略暴露了一个新的维度,我们称之为“基数”(转换集的大小))。ResNeXt是一个同构的、多分支的架构,只有几个超参数需要设置。经验表明,即使在保持复杂性的限制条件下,增加基数也能提高分类精度。当增加容量时,增加基数比向更深处或更宽更有效。
- 论文:Aggregated Residual Transformations for Deep Neural Networks
- 论文链接:https://arxiv.org/abs/1611.05431
- 代码:https://github.com/facebookresearch/ResNeXt
- PyTorch代码:https://github.com/miraclewkf/ResNeXt-PyTorch
insight
增加基数是比增加深度和宽度更有效的提高准确率的方法
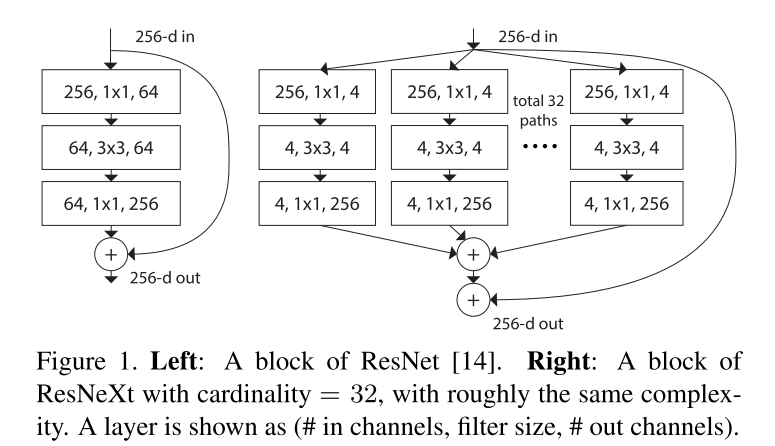
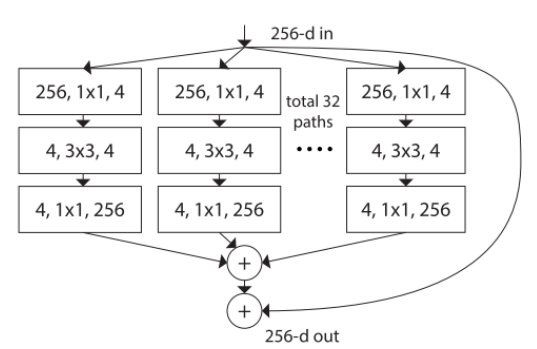
网络中的一个模块执行一组转换,每个转换都是低维的嵌入,其输出通过求和进行聚合,要被聚合的转换都是相同的拓扑,如下图右边所示,这种设计允许我们扩展到任何数量的转换,而不需要专门的设计。
图1(右)的设计是保持了图1(左)参数的复杂性和数量。即使在维持计算复杂度和模型大小的限制条件下,聚合的转换结构也优于原来的ResNet模块。
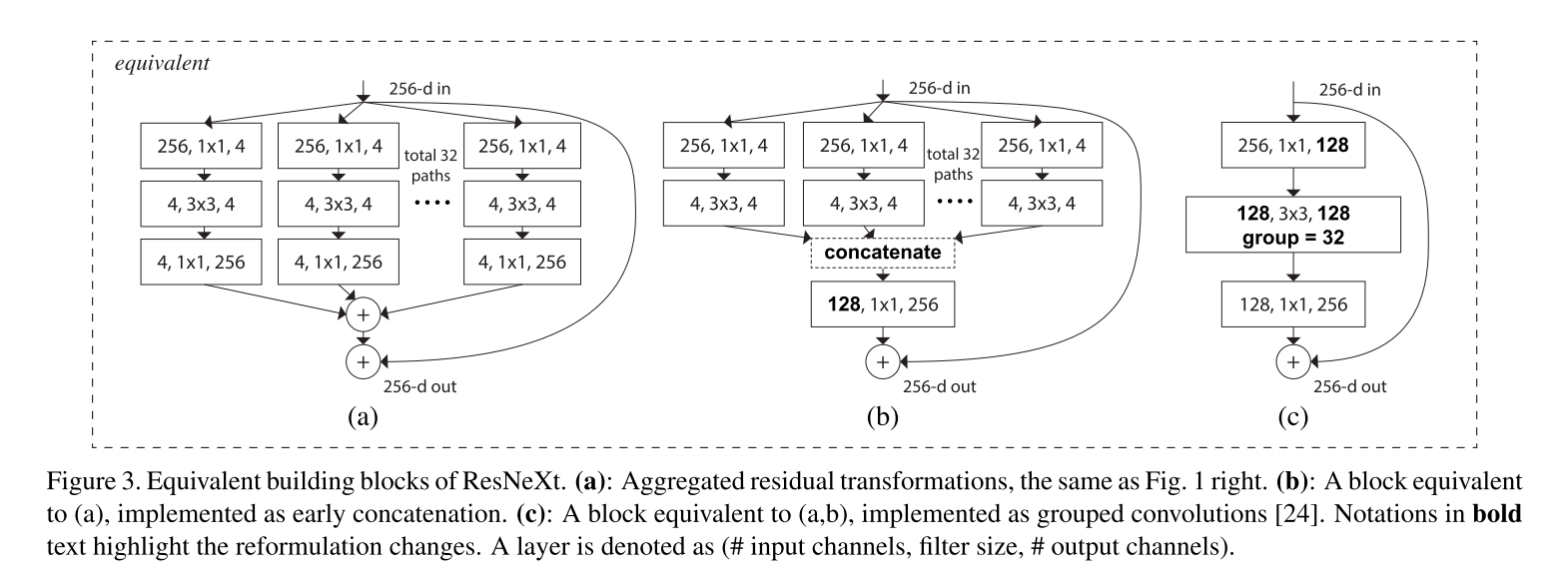
模型有两种等价形式:
- (b)中的重构与Inception-ResNet模块相似,因为它连接了多条路径;但是不同于所有已有的Inception模块,因为所有的路径共享相同的拓扑,因此路径的数量可以很容易地作为一个需要研究的因素进行隔离。
- (c)是以分组卷积进行的更简洁地表示。当分组卷积层将输入通道分成组时,分裂本质上是由分组卷积层完成的。
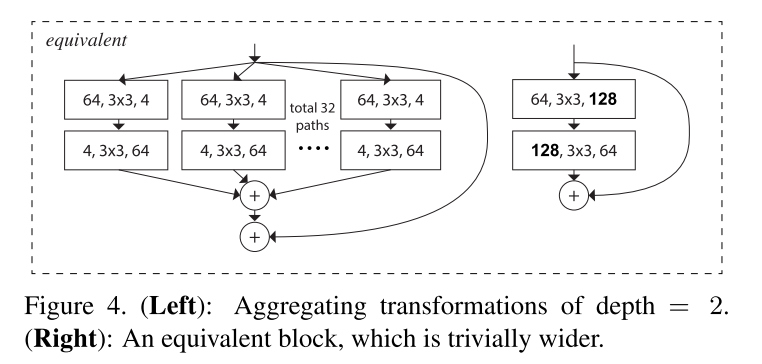
注意:只有当块深度≥3时,重构才会产生非平凡拓扑。如果块的深度为2,重构就会得到一个宽的、密集的模块。见下图。
- 在relate work中,作者提到,很少有研究利用分组卷积来提高精度。
Method
Template
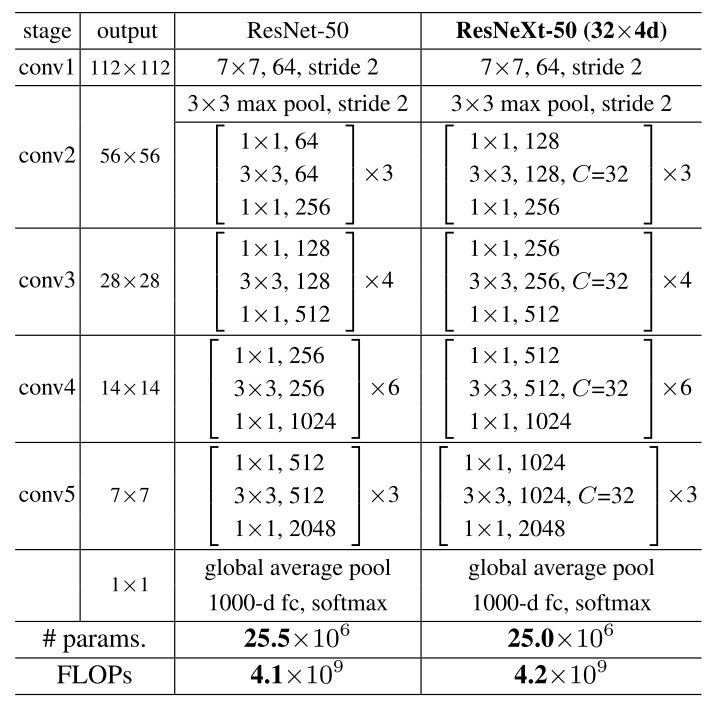
网络采用遵循VGG / ResNets的高度模块化的设计,由一堆具有相同拓扑的残差块堆叠组成。遵循两个简单的规则:
- 如果生成相同大小的feature map,则块共享相同的超参数(宽度和过滤器大小)
- 每次当空间map向下采样2倍时,块的宽度乘以2倍。(确保计算复杂性,就FLOPs(浮点操作,#乘-加)而言,对所有块大致相同)
有了这两条规则,只需要设计一个模板模块,就可以据此确定网络中的所有模块。因此,这两条规则极大地缩小了设计空间,并允许我们聚焦于几个关键因素。由这些规则,采用(c)中的重构构建的网络如下表所示:
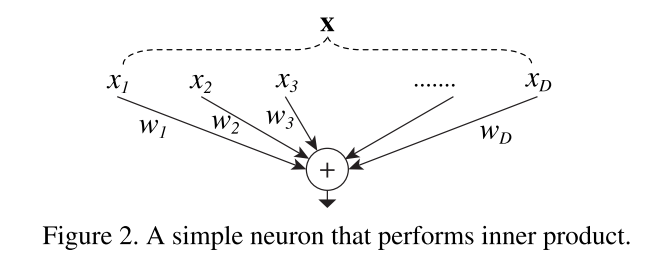
Revisiting Simple Neurons
内积可以认为是一种聚合变换的形式:![]() ,式中,
,式中,是神经元的d通道输入向量,wi是第i个通道的滤波器权值。
上面的操作可以重新定义为拆分、转换和聚合的组合:
- 分割:将向量x分割为低维嵌入,其中为一维子空间xi
- 变换:对低维表示进行变换,简单缩放:wixi
- 聚合:所有嵌入中的转换都用
进行聚合
Aggregated Transformations
用更通用的函数代替基本变换(),它本身也可以是一个网络。将聚合变换表示为:

可以是任意函数,
应该将x投影到一个(可选的低维)嵌入中,然后转换它。C是要被聚合的转换集合的大小,可以是任意数,称为基数。作者认为基数的维数控制着更复杂转换的数量。
在本文中,考虑了一种设计变换函数的简单方法:所有的具有相同的拓扑。将单个的转换
设置为瓶颈型架构。每个
的第一层1×1产生低维嵌入。
将Eqn.(2)中的聚合变换作为残差函数:
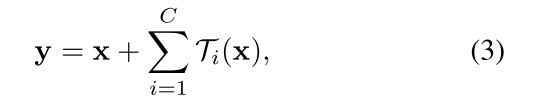
Model Capacity
参数的复杂性和数量反映了模型的内在能力,因此通常被作为深层网络的基本性质来研究。
考虑基数的影响时,方法:调整下图右侧瓶颈的宽度,因为它可以从输入和输出块中分离出来。这个策略不会改变其他超参数(块的深度或输入/输出宽度),因此有助于我们关注基数的影响。

图1(左)中,原ResNet瓶颈块[14]的参数为256·64+3·3·64·64+64·256≈70k
当瓶颈宽度为d时,我们在图1(右)中的模板有参数:C · (256 · d + 3 · 3 · d · d + d · 256)
当C = 32, d = 4时,Eqn.(4)≈70k。表2显示了基数C和瓶颈宽度d之间的关系。第二行的d表示每个path的中间channels数量,最后一行则表示整个block的宽度,是第一行C和第二行d的乘积。

Experiments
Experiments on ImageNet-1K
我们在1000种类别的ImageNet分类任务上进行了消融实验。将ResNet-50/101中所有的块替换为我们的块。
Cardinality vs. Width
首先评估基数C和瓶颈宽度之间的权衡,保留复杂性如表2所示。
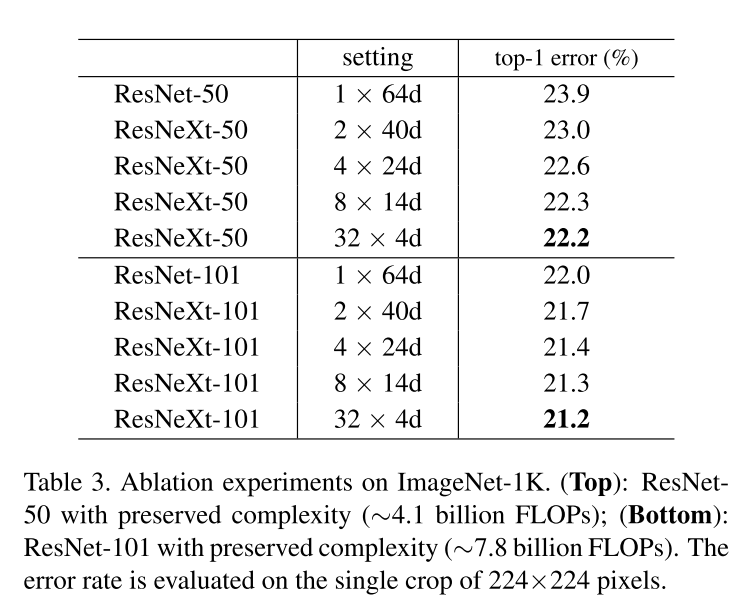
结果如下表所示,误差与epoch的关系曲线如下图所示。与ResNet-50比较,32×4d的ResNeXt-50验证误差为22.2%,比ResNet基线的23.9%降低1.7%。基数C从1增加到32,保持复杂性的同时,错误率不断降低。此外,32×4d的ResNeXt的训练误差也比ResNet的对应部分低得多,说明增益不是来自正则化,而是来自更强的表示。
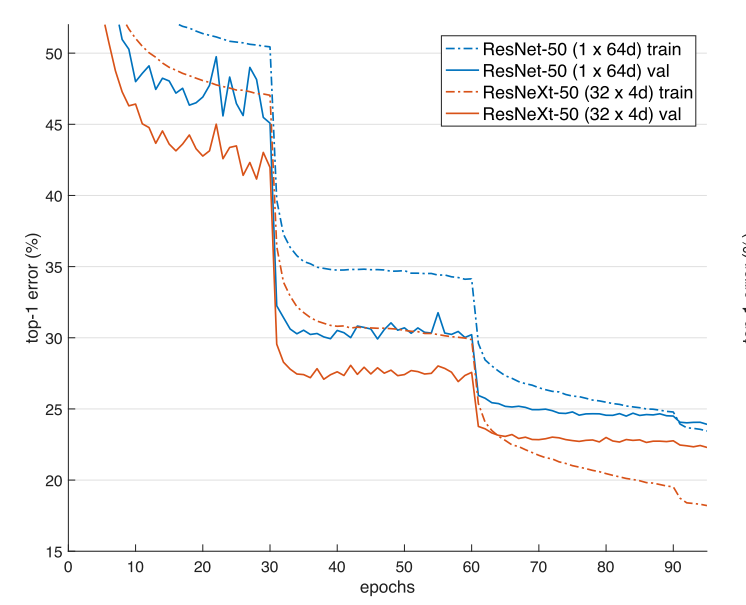
在ResNet-101中也观察到类似的趋势,其中32×4d的ResNeXt- 101比对应的ResNet-101表现好0.8%。虽然验证误差的提高比50层的情况小,但是训练error的提高仍然很大(ResNet-101为20%,32×4d的ResNeXt-101为16%)。事实上,更多的训练数据将扩大验证错误的差距,正如在ImageNet-5K集所显示的那样。
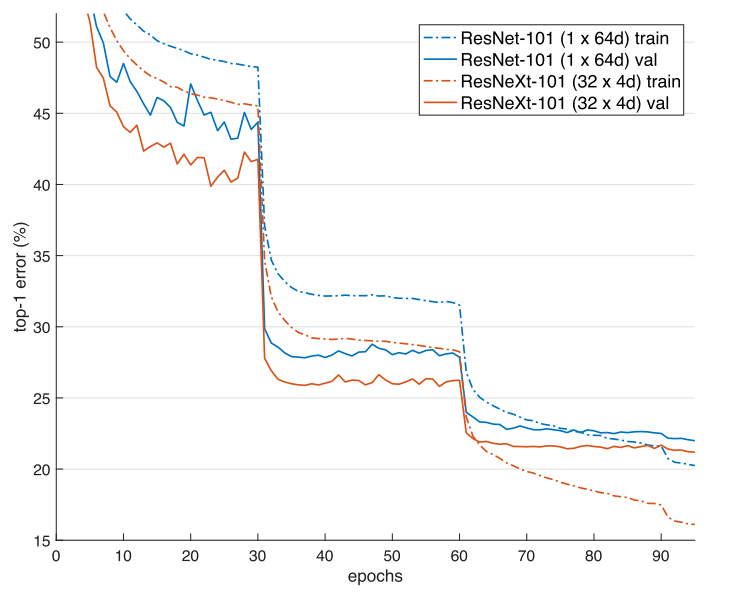
表3还表明,在保持复杂性的情况下,以减少宽度为代价增加基数,当宽度很小时,准确性趋于饱和,因此下面采用不小于4d的瓶颈宽度。
Increasing Cardinality vs. Deeper/Wider
接下来我们研究通过增加基数C或增加深度或宽度来增加复杂性。下面的比较是参照ResNet-101基线的2×FLOPs。我们比较一下下面的变种,它们有大约150亿次FLOPs。
- Going deeper:200层
- Going wider:增加瓶颈宽度
- Increasing cardinality:加倍C
表4显示,相对于ResNet-101基线(22.0%),增加2倍的复杂度可以减少错误。但是更深(ResNet- 200,上涨0.3%)或更宽(ResNet- 101,上涨0.7%)时,带来的改善很小。2×64d ResNeXt-101(即在1×64d的ResNet-101基线上,C翻倍并保持宽度)降低了top-1错误1.3%至20.7%。64×4d ResNeXt-101,将top-1的误差降低到20.4%。
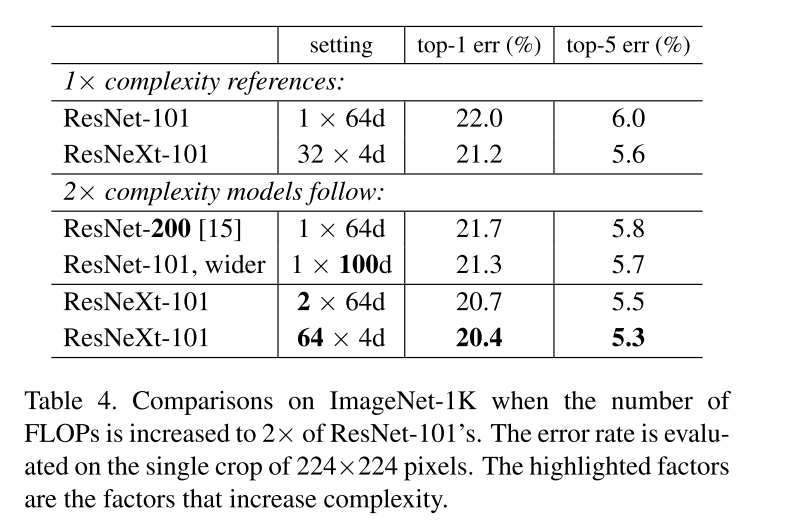
也就是说,增加C比更深更宽更有用 。
我们还注意到,32 * 4d的ResNet-101(21.2%)的性能优于更深的ResNet-200和更宽的ResNet-101,尽管它的复杂性只有约50%。这再次表明基数比深度和宽度维度更有效。
Residual connections
下表显示了剩余(shortcut)连接的效果:
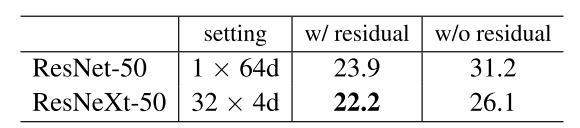
这些对比表明剩余连接有助于优化,而聚合转换是更强的表示,正如事实所示,它们始终比有或没有剩余连接的对应转换执行得更好。
Comparisons with state-of-the-art results
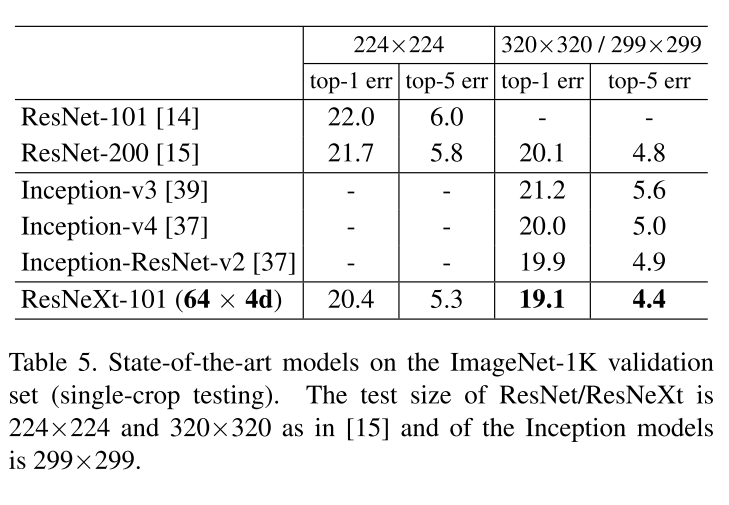
Experiments on ImageNet-5K
与ResNet-50相比,ResNeXt-50将5K-way top-1错误降低3.2%,与ResNet-101相比,ResNetXt-101将5K-way top-1错误降低2.3%。说明了ResNeXt更强的表示能力。
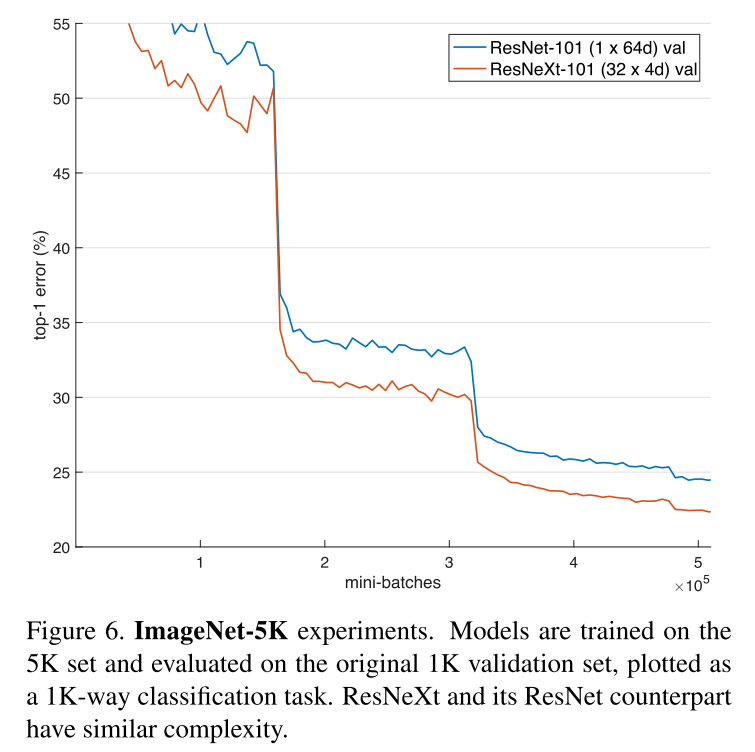
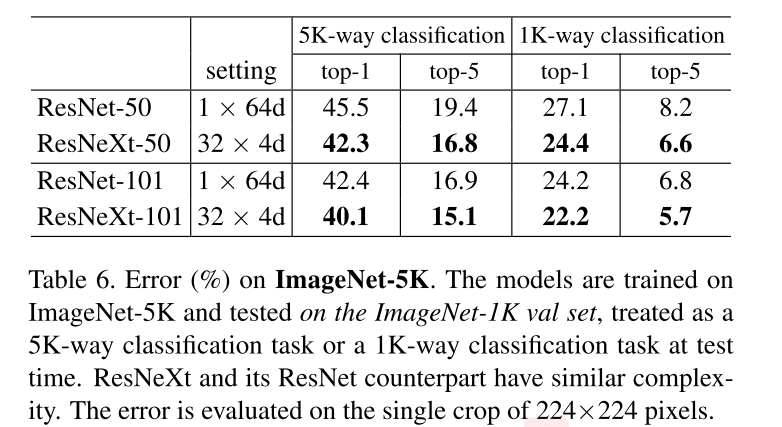
Experiments on CIFAR
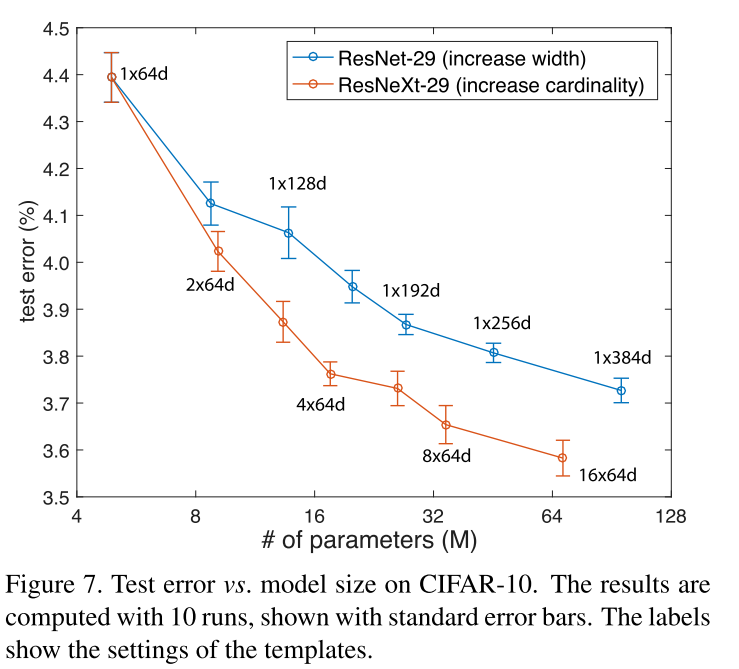
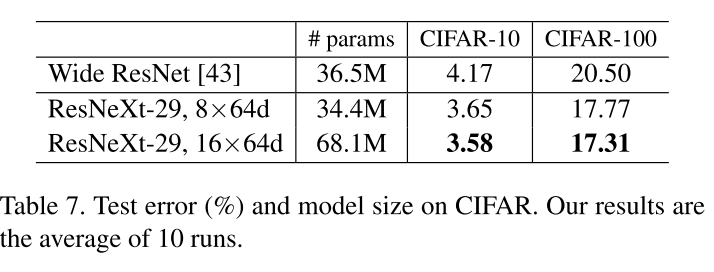
比较了两种基于基线的复杂性增加的情况:
- 增加基数并固定所有宽度,
- 增加瓶颈宽度并固定基线 = 1
Experiments on COCO object detection