多种梯度下降变体的对比：Batch gradient descent、Mini-batch gradient descent 和 stochastic gradient descent

一. 批量梯度下降（Batch gradient descent）

批量梯度下降（Batch gradient descent），是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行更新。
$θ = θ ? η · ?θJ(θ)$
由于我们需要计算整个数据集的梯度以仅执行一次更新，因此批量梯度下降可能非常缓慢，并且对于内存小而数据集庞大的情况来说很棘手。批次梯度下降法也不允许我们在线更新模型，即即时更新新示例。
批量梯度下降优点是理想状态下经过足够多的迭代后可以达到全局最优.

批量梯度下降伪代码：

for i in range(nb_epochs):params_grad = evaluate_gradient(loss_function, data, params) params = params - learning_rate * params_grad

其中nb_epoch是自己指定的迭代次数，params_grad是经过一次迭代后的参数

二. 随机梯度下降法（Stochastic Gradient Descent）

随机梯度下降法，其实和批量梯度下降法原理类似，区别在与求梯度时没有用所有的m个样本的数据，而是仅仅选取一个样本来求梯度。正是为了加快收敛速度，并且解决大数据量无法一次性塞入内存的问题，所以stochastic gradient descent（SGD）就被提出来了，SGD的思想是每次只训练一个样本去更新参数（比如样本 $j$: $(x_{(j)}^0,x_{(j)}^1,...,x_{(j)}^n)$），对应的更新公式是：
$θ = θ ? η · ?θJ(θ; x^{(i)}; y^{(i)})$
随机梯度下降（SGD）为每个训练示例 $x（i）$和标签 $y（i）$执行参数更新。

随机梯度下降伪代码：

for i in range(nb_epochs): np.random.shuffle(data) for example in data:params_grad = evaluate_gradient(loss_function , example , params) params = params - learning_rate * params_grad

因为每次只用一个样本来更新参数，会导致不稳定，每次更新的方向，不像batch gradient descent那样每次都朝着最优点的方向逼近，会在最优点附近震荡。每次训练的都是随机的一个样本，会导致导致梯度的方向不会像BGD那样朝着最优点（下图中所示）。因此我们在伪代码中加入了随机打乱数据np.random.shuffle(data)。

其实，随机梯度下降法与批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，而批量梯度下降法在样本量很大的时候，训练速度不能让人满意。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。那么，有没有一个办法能够结合两种方法的优点呢？有！这就是下面要介绍的小批量梯度下降法。

三. 小批量梯度下降法（Mini-batch Gradient Descent）

为n个训练示例的**每个小批量** (i到i+n）进行了更新。对应的更新公式是：
$θ = θ ? η · ?θJ(θ; x^{(i:i+n)}; y^{(i:i+n)})$
因此，这可以导致更稳定的收敛。常见的迷你批处理大小在50到256之间，但是会因不同的应用而有所不同。训练神经网络时，通常选择小批量梯度下降算法。
下面来看看对比图：

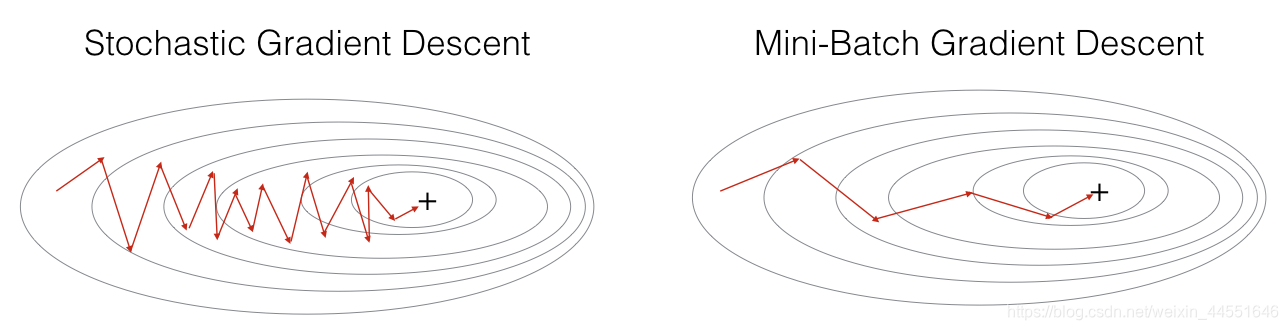
从图中能够看出，mini-batch gradient descent 相对SGD在下降的时候，相对平滑些（相对稳定），不像SGD那样震荡的比较厉害。

小批量梯度下降伪代码：

for i in range(nb_epochs): np.random.shuffle(data)for batch in get_batches(data, batch_size=50):params_grad = evaluate_gradient(loss_function, batch, params) params = params - learning_rate * params_grad

具体代码请见大佬Github

四. 梯度下降优化器