基本概念
面板数据及分类
面板数据分类:
- 短面板和长面板
- 动态面板和静态面板
- 平衡面板和非平衡面板
截面数大于时间数就是短面板,反之,则为长面板
解释变量包含被解释变量的滞后值则为动态面板,反之,则为静态面板
平衡面板:每个个体在想他的时间内都有观测值记录,For any I, there are T observations. 反之,则为非平衡面板
面板数据的优点:
1. 可以处理有不可观测的个体异质性所导致的内生性问题
2. 提供更多个体动态行为的信息
不足之处:
1. 大多数面板数据分析技术都是针对短面板
2. 寻找面板数据结构的工具变量不是很容易
面板数据模型
非观测效应模型
a.固定效应模型


b.随机效应模型

混合回归模型

面板数据模型的估计和修正方法
- 固定效应模型的估计
对固定效应模型的估计有两种方法:
固定效应变换(组内变换)与LSDV(最小二乘虚拟变量法)
a. 固定效应变换(组内变换)
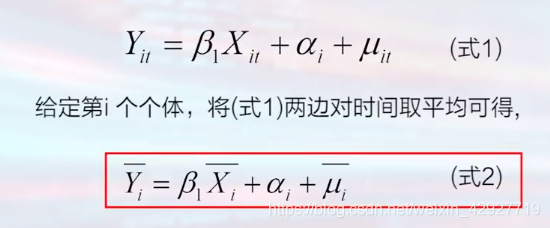

固定效应变换的优缺点
优点:即使个体效应与解释变量相关也可以得到一致估计;
缺点:无法估计不随时间而变的变量的影响。
固定效应的STATA命令
xtreg y x,fe
xi:xtreg y x i.year,fe
tab year,gen(year)
b. LSDV思想

STATA命令:
- 不存在时间效应: xi:reg y x i.code
- 存在时间效应:xi:reg y x i.code i.year
- 随机效应模型
对随机效应模型的估计方法是广义最小二乘法

STATA命令:
- 不存在时间效应:xtreg y x ,re
- 存在时间效应:xi: reg y x i.year,re
第一讲案例
- 导入数据及查看数据描述
. use "D:\traffic.dta" # 导入数据
. des #查看数据描述
显示:
obs: 336 vars: 54 30 Nov 2008 15:45
--------------------------------------------------------------------------------storage display value
variable name type format label variable label
--------------------------------------------------------------------------------
state float %9.0g sid State ID (FIPS) Code
year int %9.0g Year
spircons float %9.0g Spirits Consumption
unrate float %9.0g Unemployment Rate
perinc float %9.0g Per Capita Personal Income
emppop float %9.0g Employment/Population Ratio
beertax float %9.0g Tax on Case of Beer
sobapt float %9.0g % Southern Baptist
mormon float %9.0g % Mormon
....等等
- 描述性统计
格式: sum + 变量名
. sum beertaxVariable | Obs Mean Std. Dev. Min Max
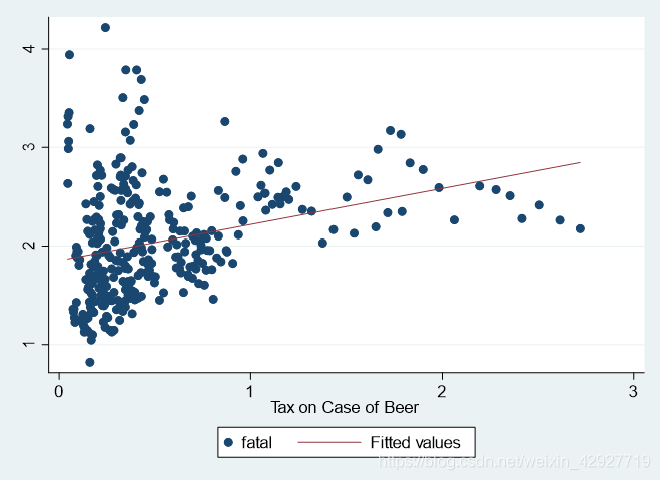
-------------+---------------------------------------------------------beertax | 336 .513256 .4778442 .0433109 2.720764twoway (scatter fatal beertax)(lfit fatal beertax) # 核心变量和被解释变量的散点图并画出回归直线
xtline fatal # 画出核心变量的时间序列图

3. 模型选择
选择PLS 还是 FE?
. tab year, gen(year)
. xtreg fatal beertax spircons unrate perinck year2-year7, fe
Fixed-effects (within) regression Number of obs = 336
Group variable: state Number of groups = 48R-sq: Obs per group:within = 0.4528 min = 7between = 0.1090 avg = 7.0overall = 0.0770 max = 7F(10,278) = 23.00
corr(u_i, Xb) = -0.8728 Prob > F = 0.0000------------------------------------------------------------------------------fatal | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------beertax | -0.435 0.154 -2.82 0.005 -0.738 -0.132spircons | 0.806 0.113 7.15 0.000 0.584 1.028unrate | -0.055 0.010 -5.31 0.000 -0.075 -0.035perinck | 0.088 0.020 4.41 0.000 0.049 0.128year2 | -0.053 0.030 -1.77 0.078 -0.113 0.006year3 | -0.165 0.037 -4.40 0.000 -0.239 -0.091year4 | -0.200 0.042 -4.80 0.000 -0.282 -0.118year5 | -0.051 0.052 -0.99 0.325 -0.152 0.051year6 | -0.100 0.059 -1.69 0.091 -0.216 0.016year7 | -0.134 0.068 -1.98 0.049 -0.267 -0.001_cons | 0.129 0.431 0.30 0.765 -0.720 0.978
-------------+----------------------------------------------------------------sigma_u | 1.0987683sigma_e | .14570531rho | .98271904 (fraction of variance due to u_i)
------------------------------------------------------------------------------
F test that all u_i=0: F(47, 278) = 64.52 Prob > F = 0.0000- 模型检验
截面相关检验
. xtcsd, pes
Pesaran's test of cross sectional independence = -1.716, Pr = 1.9138
如果截面相关
