一：概述
矩阵分解我学过的挺多种，比如极分解，谱分解，满秩分解，正交三角分解还有这里的直接三角分解大部分我都没有具体运用的经验。但是这里的三角分解的应用就很直白了，就是把矩阵分解为规律的三角矩阵后，我们就能用上次上篇文章里那种解出一个值然后不断回代的方式得到方程组的解。
二：具体步骤
计算方法课上老师只讲了一个很机械的方法，先用一个例子说明吧（带下标的通式打起来费劲看着也费劲）。
图一
我们可以通过如下步骤使之变成两个三角矩阵的乘积。
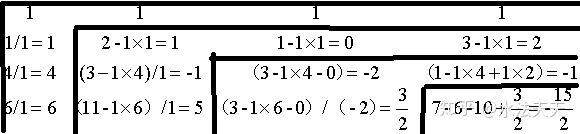
图二
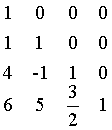
矩阵L
矩阵U
已知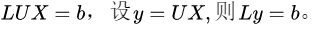
使用两次回代公式，
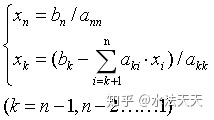
第一次求出y，第二次求出x。
三：原理分析
图二中的计算步骤很容易理解，线性代数课程中我们学习过求标准正交基的施密特方法，于是很容易联想到上述计算步骤的原理：
（1）首先提取出矩阵列向量：
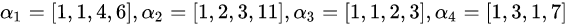
（2）然后从第一行开始把主元素上方的元素消去化为0，并把主元素化为1：
（3）再从上式中反解出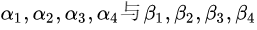
的关系，很容易得出矩阵L即为
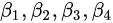为列空间组成的正交矩阵，矩阵U为从
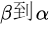的过渡矩阵。
（实际上正交三角分解即为把上述步骤替换为施密特方法，而上文这种正交化方法叫啥，评论区有大神可以告诉我一下）
（查到了，叫Dolittle分解，如果矩阵L对角元不进行单位化，称为Courant分解。）
四：算法实现（MATLAB）
function [L,U,y,X] = LU_fenjiefa(A, b)
%采用直接三角分解法解线性方程组，思路如下:
%求方程组AX=b的解，把A进行分解A=LU，LUX=b
%设y=UX，则Ly=b,先求出y再求X。%% 第一步：初始化L与U矩阵
[a1, a2] = size(A);
for r = 1:a2 %给上三角阵U的第一行赋值U(1,r) = A(1,r);
end
L(1,1) = 1; %给下三角阵L的第一列赋值
for r = 1:a2 L(r,1) = A(r,1)/U(1,1);L(r,r)=1;
end %第二步：Dolittle法求下三角矩阵L、上三角矩阵U
for k = 2:a2 %k为列数，一列一列地求for i =2:k %i为U矩阵中的行数s1=0;for r=1:k-1s1=s1+L(i,r)*U(r,k);endU(i,k)=A(i,k)-s1;endfor j=k+1:a1 %j为L矩阵中的行数s2=0;for r=1:k-1s2=s2+L(j,r)*U(r,k);endL(j,k)=(A(j,k)-s2)/U(k,k); %对主元素单位化end
end%% 第三步：求y Ly=b
y(1)=b(1); %下三角矩阵从第一行开始解for i=2:a1 s3=0;for j=1:i-1s3 =s3+L(i,j)*y(j);endy(i) = (b(i)-s3);
end
% 第四步：求X UX=y
X(a1)=y(a1)/U(a1,a2);
for i=a1-1:-1:1s4=0;for j=i+1:a1s4 =s4 +U(i,j)*X(j);endX(i) = (y(i)-s4)/U(i,i);
end
五：总结
刚学的时候对这种计算方法只是机械的记忆，今天要写这篇文章的时候才对计算的原理思考了一下，其实类比施密特正交化，我们很容易就能想到。
（插个旗子：计算方法课程笔记结束后，开一篇文章，专门研究一下各种矩阵分解的应用，应该很有趣）