privacy-preserve deep learning

背景：
大规模搜集数据来进行深度学习造成了严重的隐私问题。
带来的问题：
1.收集这些数据的公司会永远保存这些数据；从中收集数据的用户既不能删除这些数据，也不能控制如何使用这些数据，也不能控制从他们的数据中学习到的多少。
2.图像和语音记录往往包含意外捕捉到的敏感物品面部、车牌、电脑屏幕、他人说话的声音和环境噪音等。
3.公司保存的用户数据要接受传票和搜查令，以及国家安全和情报机构的无担保间谍活动
4.互联网巨头对从数百万用户收集的“大数据”的垄断导致了他们对从这些数据中学习到的人工智能模型的垄断。

这篇论文的主要创新点在于有选择的共享模型的参数。
这种参数共享的方法，使得即使没有额外的保护，已经实现了比任何现有的方法都更强大的隐私。系统中唯一的泄漏不是直接显示所有训练数据，而是通过一小部分神经网络参数间接泄漏。为了尽量减少这种泄漏，我们展示了如何使用稀疏向量技术将差异隐私应用于参数更新，从而减少由于参数选择（即，选择要共享的参数）和共享参数值造成的隐私损失。

该论文中深度学习系统的架构：
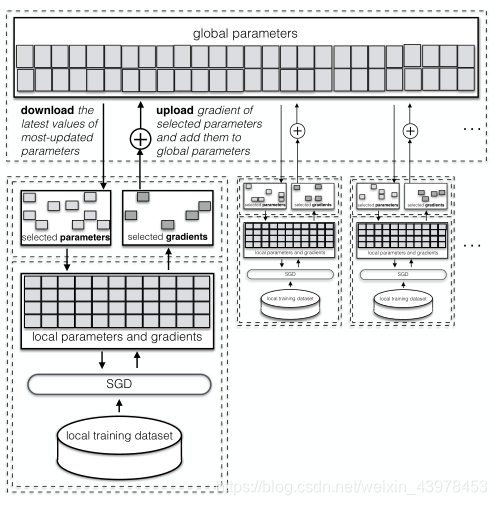DSSGD假设两个或多个参与者同时独立训练。在每一轮local training之后，每个参与方都可以异步选择梯度进行共享（上传）。每个参与方可以控制需要上传的梯度的个数以及共享的频率。中心服务器可以根据上传的梯度更新相应的参数。

元参数：

DSSGD在各个参与方中的过程

选择初始化参数 $w^{(i)}$和学习率α
repeated：
（1）从server上下载 $θ_d$x $w{(i)}$的参数并替换相应的本地参数。
（2）在本地数据集上跑SGD，并更新 $w{(i)}$.
这里的SGD一般采用mini-batch SGD（随机选择一组大小为M的batch），当然，也可以使用SGD。
（3）对于所有的parameters计算其梯度 $△w^{(i)}$
（4）上传 $△w_s^{(i)}$到server.
那么，到底应该如何上传呢？上传多少呢？
论文中提到了两种上传梯度的方案：
（1）选取对模型贡献最大的 $θ_u$的梯度进行上传。即S= $θ_u|w^{(i)}|$.
（2）将梯度值高于阈值τ的上传
注意：在上传 $△w^{(i)}$之前，他们的值被截断在[-γ，γ]之间，并且为了防止隐私泄露得多，可以在上传之前添加噪声。其实也就是是之在一个范围[ $△w^{(i)}$,γ]之间，并且加上噪声之后再上传。

参数服务器
处理上传和下载请求，并根据上传的梯度相应的更新global parameters和计数器。（为了使得最近更新的参数的权重更大，可以周期性的将计数器乘衰减因子β，即stat*β）

思考：为什么分布式随机梯度下降可以达到一个好的效果呢？
原因：和随机梯度下降相比较于批梯度下降有异曲同工之处。
训练过程中用全局参数子集更新局部参数，提高了局部SGD的随机性，这对于防止本地SGD过度拟合其小型本地数据集起着至关重要的作用。单独训练时，每个参与者都容易陷入局部最优。用其他参与者学习的值覆盖本地学习的参数，这些参与者在不同的数据集上进行训练，有助于每个参与者避开本地优化，并使他们能够探索其他值，从而得到更精确的模型。

DSSGD中参数服务器的过程

初始化 $w^{(global)}$，将计数器向量置0
事件：上传 $△w_s$
更新相应的参数，计数器+1。即：
$w^{(global)}:=w^{(global)}+△w_j$ $stat_j:=stat_j+1$
事件：download
对计数器进行排序，将其中stat_j最大的其中的 $θ_d$的下载下去。

该论文中使用的数据集：
1、MNIST（手写数据集）：3232的图像，60000个训练集，10000个测试集。
2、SVHN（谷歌街景数据集）：3232的图像，有600000个数据，论文中使用100000个来训练，10000个数据来测试。

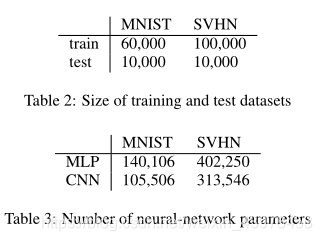
规范化数据：
减去训练样本中的平均值并除标准差来规范化数据。
论文中对两个数据集的神经网络的输入层分别是1024和3072。

论文中使用了两种神经网络结构来进行测试：
1、MLP（多层感知器）
2、CNN（卷积神经网络）

图5（MLP）和图6和图7（CNN）中提供了我们的网络架构的精确规范：

在该论文的实验中，实现了两个选择要传到参数服务器的梯度的标准。
1、在最大值的情况下，每个参与者上传上一个本地训练时期绝对值最大的梯度。
2、参与者上传值超过阈值的梯度随机样本。
对于下载，每个参与者都会选择经过最多更新的参数。

在论文的实验中，选择下载的参数比例为1，也就是将参数全部下载下来。

不同元参数值（小批量大小和共享梯度的分数）的SGD和SSGD

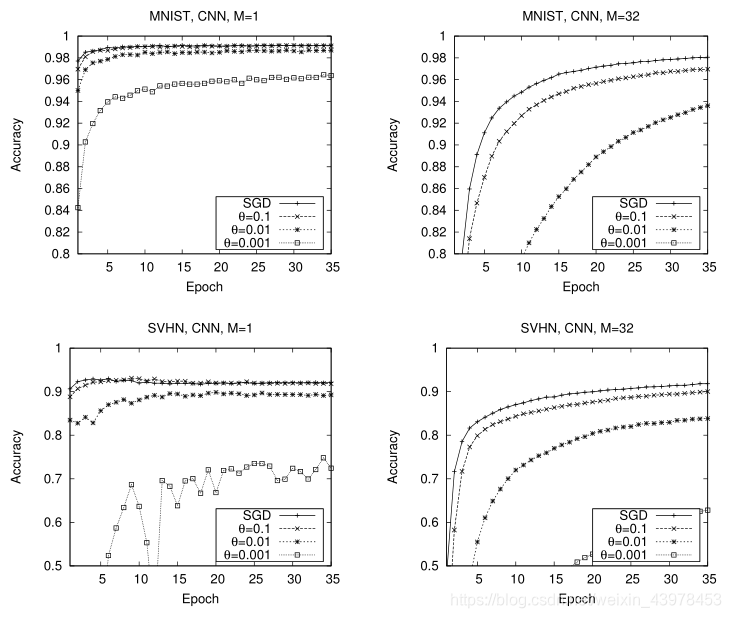
从上面的图可以发现：
将mini-batch 的size设置为1在整个训练过程中实现了很高的随机性，收敛速度非常快，但也会导致一些曲线的波动。当mini batch 的size设置为32时，由于在梯度下降期间对许多训练数据点应用梯度平均值，收敛速度较慢但更平滑。

SSGD在CNN和MLP网络架构和不同参数共享率下实现的最大精度。结果与独立精度进行了比较。最小批量大小为1。

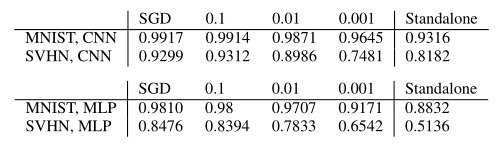
从上表可以发现：
通过在每个梯度下降步骤共享一小部分梯度，我们可以获得比独立SGD更好的精度。这也充分说明了该论文所提出的方案的优势。

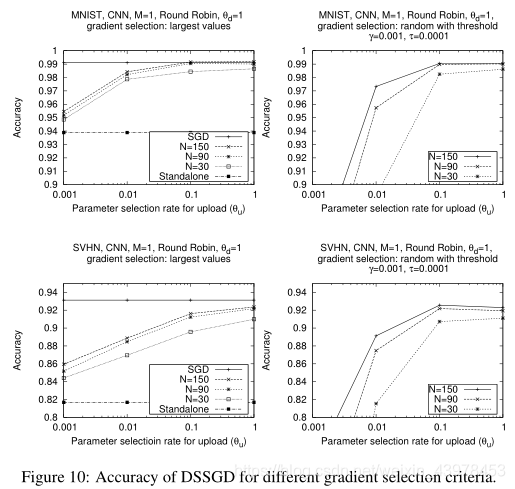
通过上面两个图可以发现：参与者的数量对准确性的影响低于共享参数的百分比。这表明分布式SSGD不需要很多参与者来提高准确性。

注意：所有上述结果都是假设每个参与者与其他参与者共享其最大梯度而获得的。（因为还有另外一种共享梯度的选择方法：高于阈值τ的梯度）

下图显示了不同数据集、学习率和参与者数量的DSSGD的收敛性
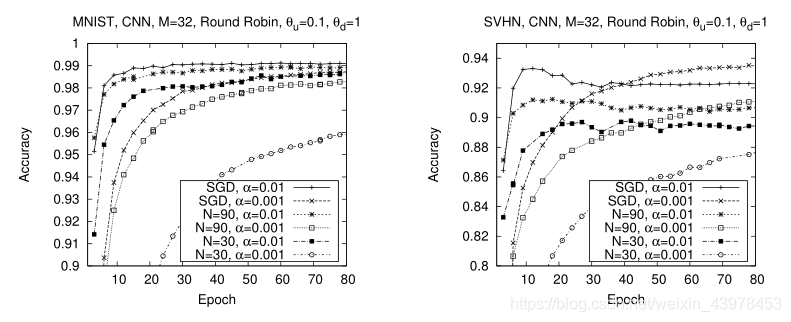从上图可以发现：
无论参与者人数多少，较高的学习率确实会导致更快的收敛到最大精度。因此，DSSGD的分布性和选择性不会改变梯度下降算法的整体性能。

最后，论文还提到隐私问题，论文中主要使用差分隐私技术来防止隐私的泄露。

传统深度学习中的几个隐私问题：
（1）所有的训练数据都揭露给第三方，数据拥有者没有对数据的控制权。
（2）数据所有者无法控制学习目标（即正在训练哪个模型），因此无法控制甚至不知道从数据中推断出什么。例如，一个人可能愿意分享她的图像用于人脸识别，但不愿意从背景对象推断她的位置。
（3）在传统的深度学习中，学习模型不能直接提供给数据所有者。如果他们想使用它，他们必须向持有模型的公司透露他们的输入，从而使他们面临与培训数据相同的隐私风险。

该论文防止了直接泄露和间接泄露的两种情况：
（1）直接泄露
在训练模型的时候： 参与者不会向任何人透露他们的培训数据集，从而确保他们的数据具有很强的隐私性。本地数据集的大小和动态是保密的，并且在每一轮SSGD中可以使用不同的数据样本。参与者还可以随时删除其培训数据。
在使用模型的时候： 所有参与者在本地和私下使用模型，无需与其他参与者进行任何通信，也无需向任何人透露输入数据或模型的输出.
（2）间接泄露
参与者可以通过公开更新一小部分神经网络参数，间接地揭示一些关于他们训练数据集的信息。所以该论文中使用差异隐私来确保参数更新不会泄露关于训练数据集中任何单个点的太多信息。

差分隐私

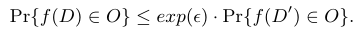
在该论文中，f计算参数梯度并选择要与其他参与者共享的参数梯度。 潜在泄漏有两个来源： 如何选和选了谁。
为了缓解这两种类型的泄漏，在一致的差分隐私机制下，我们使用 稀疏向量技术来随机选择一小部分梯度值高于阈值的梯度，并且共享所选梯度的扰动值。

首先，每个参与者j的每个epoch的总隐私预算都定为ε===》将ε分成c部分，其中c=可以上传的梯度的数量，即： $c=θ_u|△w|$，即对于每一个参与者的每一个可上传的参数j的梯度，其预算为 $\frac{ε}{c}$===》将每个上传值的预算分为两部分：1、检查对于随机参数j的梯度 $△w_j^{(i)}$是否大于阈值τ，对其分配的预算为 $\frac{8}{9}\frac{ε}{c}$，2、真正release的梯度，其预算分配为 $\frac{2}{9}\frac{ε}{c}$

使用拉普拉斯机制在选择和上传时根据分配的预算来添加噪声。
噪声取决于预算和每个参数梯度的敏感度
在该论文中，假设所有参数的梯度的敏感度都是相同的，那么噪声的大小就仅仅取决于所分配的预算。