实验(一)
研究设计:
- 选取由高一、高二、高三组成的265名高职学生,对他们进行心理测试,维度如下:
- 学生填写的分类信息包括:年级、性别、是否为独生子女。
- 身体与体育竞赛适应、陌生情境与学习情境适应、考试焦虑情景适应、群体活动适应、心理适应总分(由前四个维度相加可得到)、自我认同感总分。
研究需求:
- 需求一:根据下面的常规模型对每个学生的每个维度进行分类,并且测量在各个维度当中学生的平均值、所占百分比、最大值、最小值等基本信息(其中男生与女生要进行分开测量)。
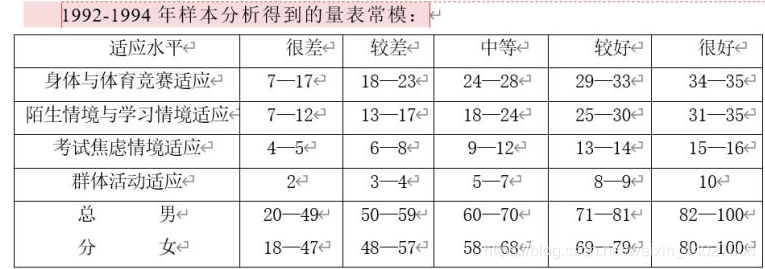
- 需求二:观察不同年级、不同性别以及是否为独生子女在这六个项的得分中是否存在显著差异,如果有差异,进一步探索哪个组与哪个组存在差异。
- 需求三:观察自我认同感的得分是否与其他5项得分存在一定的相关性,如果相关,观察相关的强度与相关的方向。
- 需求四:观察自我认同感得分的变化是否会影响到心理适应总分的变化。
构思:
- 需求一:起初原始数据当中只有每个项目的分数,而没有分组的这个维度。所以若要实现这个需求,我们必须要在每项后面分别按照常规模型去增加一个变量。这样一来,我们在每项上就拥有了两个维度。那么通过SPPS中的均值分析就可以实现这一需求。
- 需求二:首先要想探索两个及以上的独立组别之间在某一项得分上是否有差异。首先要进行正态检验与方差齐性检验。因为服从正态分布或服从近似正态分布且方差齐性和不服从正态分布的数据,所要采取的差异分析方式是不同的。若数据服从正态分布且方差齐,观察两个独立组别之间在某一项得分上是否有差异可以使用独立样本t检验。而数据若不服从近似正态分布,如果再继续使用独立样本t检验就很难保证结果的准确性。因此,要转而采用非参数检验当中的两个独立样本检验中的Mann-Whitney U检验(两个独立样本检验)。
- 需求三:由于要进行相关性检验的两个变量都属于连续变量,因此选择Pearson检验。
- 需求四:该项需求本希望采用一元线性回归。但是在进行一元线性回归是发现,结果当中的R方和调整后的R方远远低于正常可接受的水平,同时DW检验的结果远远的小于2,即意味着自变量可能自己对自己也会产生干扰,因此,采用这样的方法所得出来的结果是非常的不可信的。目前还没有找到解决办法…
实施:
- 需求一:设计好每个分组之后只要得出在每个分组上有多少人,平均值,中位数,最大值,最小值即可。在SPSS中实现这个需求只需要选择均值,然后将所需的数据放入框内即可。
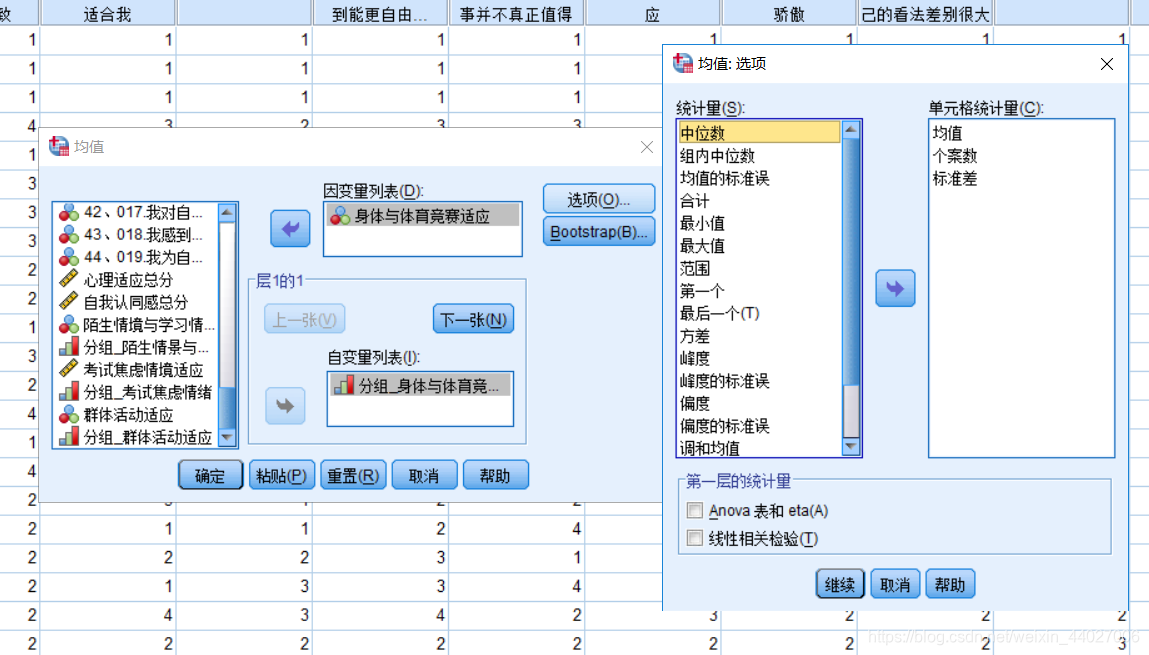
结果输出:
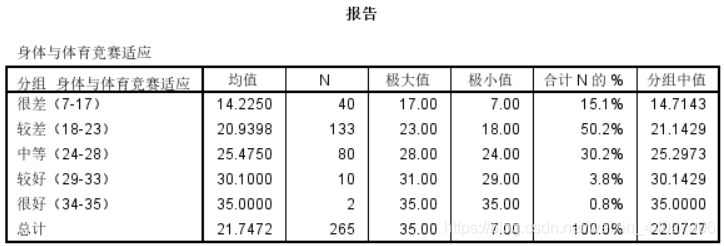
- 需求二:进行正态检验的方法有很多(比如:偏度和峰度、S-W检验(小样本<100)、K-W检验(大样本)、Q-Q图、P-P图),经过检验后发现所有数据都不服从正态分布。因此改用非参数检验中的Mann-Whitney U检验来进行两个独立组之间差异的分析。采用Kruskal-Wallis H(K)来检验三组及以上的独立组之间的差异,然后再进一步采用两两比较,来观察哪两组之间存在差异,最后取中位数来确定是何种差异。下面以年级为例:
首先检验是否为正态:
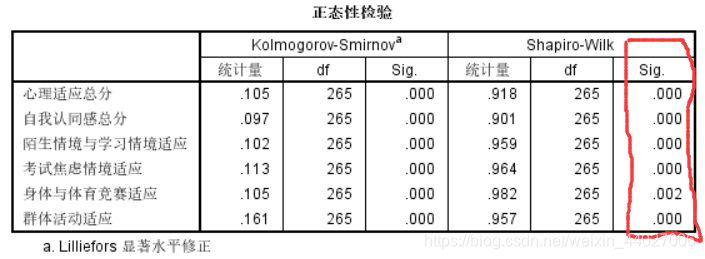
不服从正态分布,因此要采用非参数检验法:
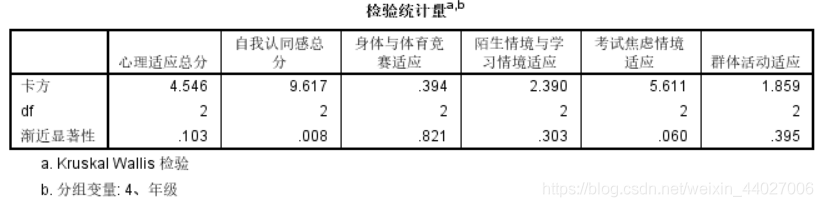
发现各个年级之间仅在自我认同感总分上有显著差异,因此进一步用两两比较来探索哪些方面具有差异。
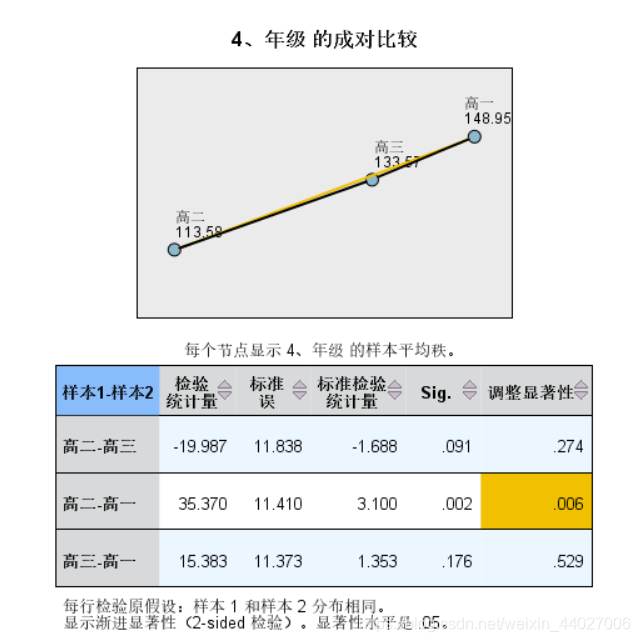
发现高一年级与高二年级之间在自我总分之间有差异,进而采用取中位数的方法来探索这两组的具体差异。
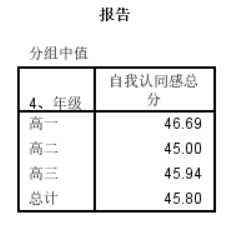
可发现高一的学生在自我认同方面的得分显著的高于高二的学生。 - 需求三:采用Pearson相关性检验即可
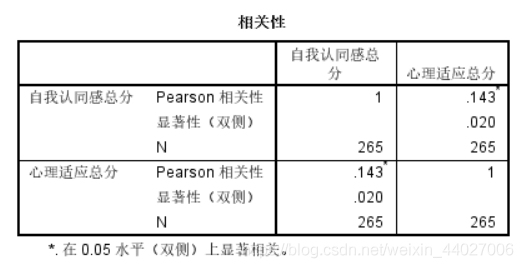
结果显示,自我认同感总分与心理适应总分呈现显著相关。但是相关的程度从Pearson相关性可以看出为极弱,即这条线比较细。
- 需求四:待解决
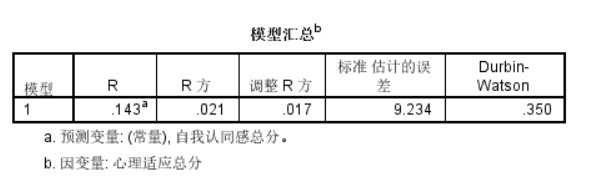
D-W值离2比较远,且R方,即拟合度极低。
实验(二)
研究设计:
- 需求一:选择24名被试,分为实验组与对照组,每组分别为12人。先对两组在同一时间进行实验前测,然后对实验组进行一段时间的心理辅导(6周左右),再次同时对实验组与对照组进行测试。
研究需求:
- 心理辅导是否会使得学生在这6项得分上能够有所提高,使得实验前和实验后出现显著差异
构思:
- 需求一:首先我对每组数据都进行了正态性检验与方差齐性检验,发现每组数据都服从近似正态分布,且方差齐。因此,接下来就是选择分析方法。由于我的目的是要测试,进行心理辅导是否会提高学生在各项得分的提升。因此我要把每个测试项分为4组(A1:实验组前测;A2:实验组后测;B1:对照组前测;B2:对照组后测)。然后对每一个组进行重复测量方差比较,即在每一项上,A1与A2比,A1与B1,B2比,A2与B1,B2比,B1与B2比。理想化一点:A1要与B1、B2没有显著差异,且A1与B1、B2互相之间不完全相等,A2与A1、B1、B2应有差异。(因为测试的时间不一样。比如:经历过爆炸或者恐怖事件的人,他们即使没有接受过心理辅导,在一段事件之后他们的恐慌程度也会降低,只是可能受过心理辅导的人降低的程度更大。)
过程:
- 需求一:首先将每个项的数据进行重新整理,分为A1、A2、B1、B2四组,然后检验是否为正态分布。然后根据正态检验结果选择重复测量方差检验的方法。
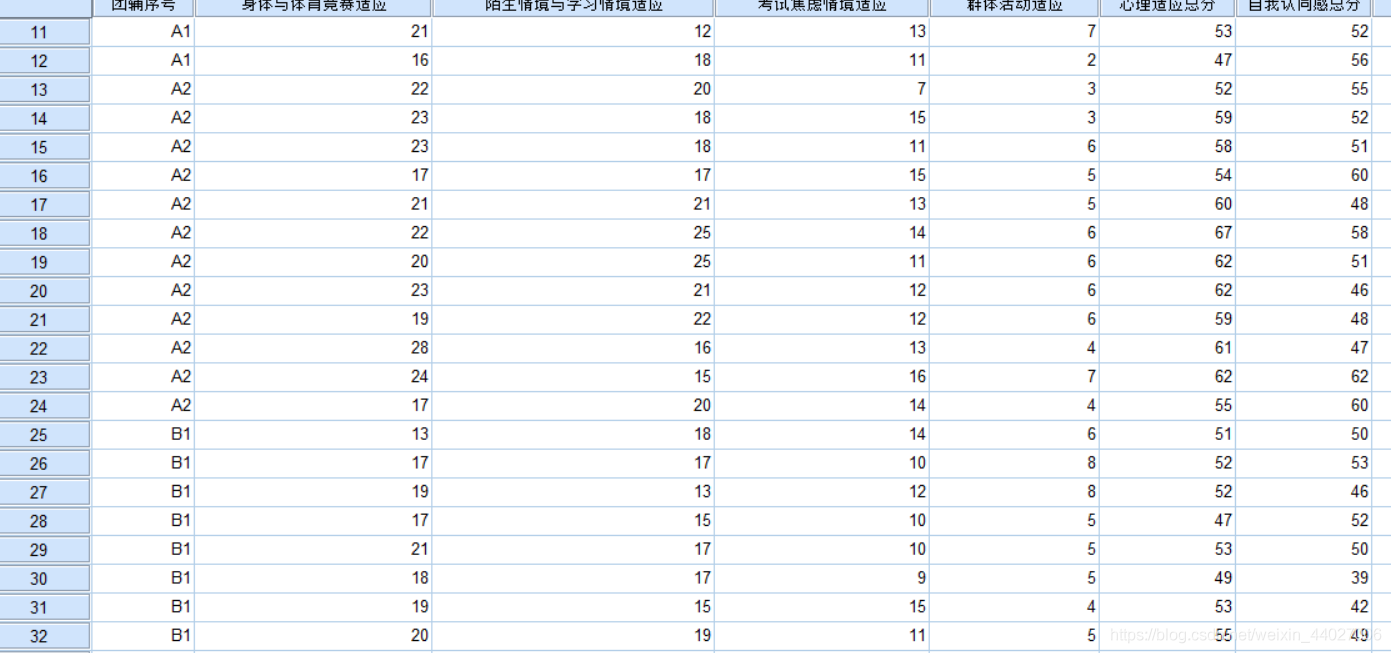
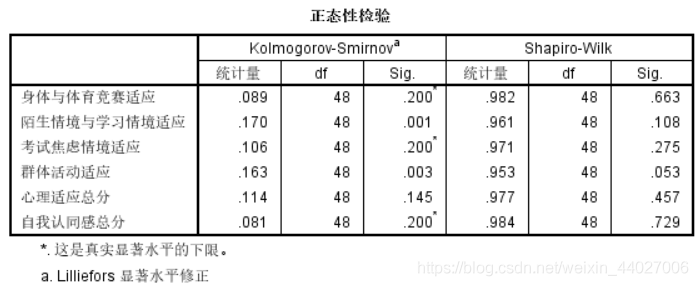
结果均服从正态分布,因此我们可以选择单因素 One-Way ANOVA进行重复测量方差检验分析。
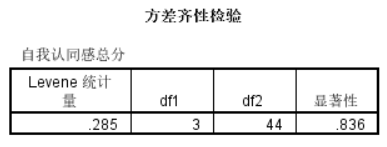
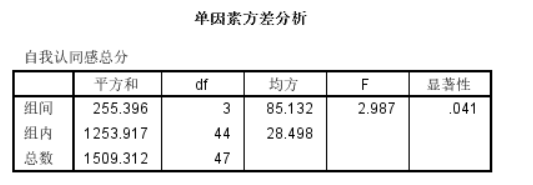
方差齐,且组间存在差异,因此进行多重比较
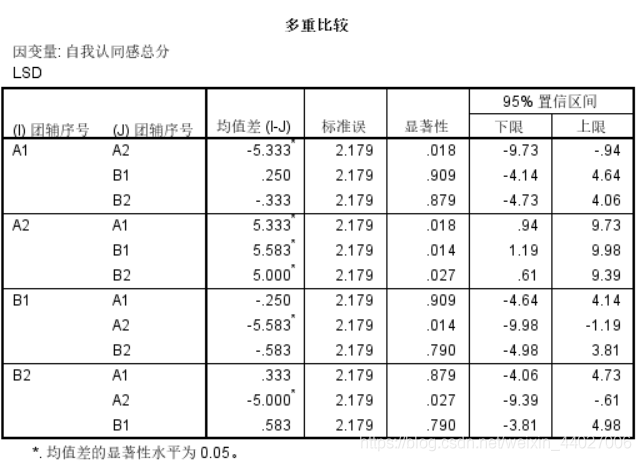
结果表明:A2与其他组均存在显著差异,并且其他组之间不存在显著差异。