

设增加的值为x,带入式子化简可得:
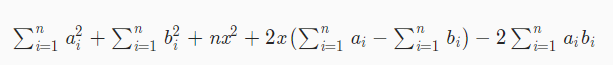
如果我们枚举x,那么整个式子只有最后一项是未知的。令整个式子最小,所以最后一项最大,所以我们需要求最后一项的最大值。
如果我们把b反转一下,那么最后一项就是卷积的形式了,所以直接FFT求出。
因为是成环的,所以我们把a复制一下,放到后面,然后FFT之后,n+1 -> 2*n 的每一项都代表选择之后的值,取最大值即可。
AC代码:
#pragma GCC optimize("-Ofast","-funroll-all-loops")
#include<bits/stdc++.h>
//#define int long long
using namespace std;
typedef long long LL;
const int N=6e5+10;
const double PI=acos(-1.0);
int n,m; LL a2,b2,a_2,b_2,res=1e18,t;
int r[N],lim,l;
struct Complex{double x,y;
}a[N],b[N];
Complex operator + (Complex a,Complex b){return {a.x+b.x,a.y+b.y};}
Complex operator - (Complex a,Complex b){return {a.x-b.x,a.y-b.y};}
Complex operator * (Complex a,Complex b){return {a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
inline void FFT(Complex *a,int n,int k){for(int i=0;i<n;i++) if(i<r[i]) swap(a[i],a[r[i]]);for(int mid=1;mid<n;mid<<=1){Complex wn={cos(2*PI/(mid<<1)),k*sin(2*PI/(mid<<1))};for(int i=0;i<n;i+=(mid<<1)){Complex w={1,0};for(int j=0;j<mid;j++,w=(w*wn)){Complex t0=a[i+j],t1=w*a[i+mid+j];a[i+j]=t0+t1;a[i+mid+j]=t0-t1;}}}if(k==-1) for(int i=0;i<n;i++) a[i].x=a[i].x/n+0.5;
}
inline void init(int n){lim=1,l=0; while(lim<=(n)) lim<<=1,l++;for(int i=0;i<lim;i++) r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
}
signed main(){cin>>n>>m;for(int i=1,x;i<=n;i++){scanf("%d",&x); a2+=x*x; a_2+=2*x; a[i].x=a[i+n].x=x;}for(int i=1,x;i<=n;i++){scanf("%d",&x); b2+=x*x; b_2+=2*x; b[n-i+1].x=x;}init(3*n);FFT(a,lim,1); FFT(b,lim,1);for(int i=0;i<=lim;i++) a[i]=a[i]*b[i];FFT(a,lim,-1);for(int i=1;i<=n;i++) t=max(t,2LL*(LL)a[i+n].x);for(int i=-m;i<=m;i++) res=min(res,a2+b2+a_2*i-b_2*i+i*i*n);cout<<res-t;return 0;
}