梯度下降Gradient-Descent

---

title: Gradient Descent
date: 2020-01-12 12:41:33
tags: [Gradient Descent]
categories: Machine Learning

梯度下降（Gradient Descent）

1.1梯度下降概述(Overview of gradient descent)

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数
$J(\theta_0,\theta_1)$
的最小值。

梯度下降的思想：开始我们随机选择一个参数的组合 $(\theta_0,\theta_1,......,\theta_n)$计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

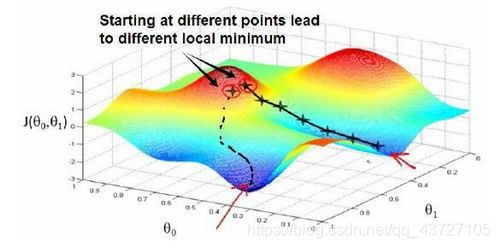
想象一下你正站立在山的这一点上，站立在你想象的公园这座红色山上，在梯度下降算法中，我们要做的就是旋转360度，看看我们的周围，并问自己要在某个方向上，用小碎步尽快下山。这些小碎步需要朝什么方向？如果我们站在山坡上的这一点，你看一下周围，你会发现最佳的下山方向，你再看看周围，然后再一次想想，我应该从什么方向迈着小碎步下山？然后你按照自己的判断又迈出一步，重复上面的步骤，从这个新的点，你环顾四周，并决定从什么方向将会最快下山，然后又迈进了一小步，并依此类推，直到你接近局部最低点的位置。

梯度下降特点：越接近最小值，步长越小，下降速度越慢。

注意区分几个常用函数：

1.损失函数（Loss Function）：定义在单个样本上，计算的是一个样本的误差；

2.代价函数（Cost Function）：定义在整个训练集上，是所有样本误差的平均，也就是损失函数的平均；

3.目标函数（Object Function）：最终要优化的函数，等于Cost Function+正则化项。

1.2 批量梯度下降（Batch gradient descent）

批量梯度下降（batch gradient descent）算法的公式为：

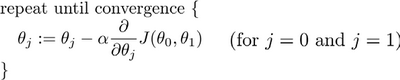
其中是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

在梯度下降算法中，还有一个更微妙的问题，梯度下降中，我们要更新 $\theta_0$和 $\theta_1$ ，当 $j=0$ 和 $j=1$时，会产生更新，所以你将更新 $J(\theta_0)$和 $J（\theta_1）$。实现梯度下降算法的微妙之处是，在这个表达式中，如果你要更新这个等式，你需要同时更新 $\theta_0$和 $\theta_1$，我的意思是在这个等式中，我们要这样更新：

$\theta_0$:= $\theta_0$ ，并更新 $\theta_1$:= $\theta_1$ 。

实现方法是：你应该计算公式右边的部分，通过那一部分计算出和的值，然后同时更新 $\theta_0$和 $\theta_1$。

在梯度下降算法中，这是正确实现同时更新的方法。这里不打算解释为什么你需要同时更新，同时更新是梯度下降中的一种常用方法。我们之后会讲到，同步更新是更自然的实现方法。当人们谈到梯度下降时，他们的意思就是同步更新。

如果你已经修过微积分课程，如果你熟悉偏导数和导数，这其实就是这个微分项：
$\alpha \frac{\partial J(\theta_0,\theta_1)}{\partial\theta_0},\alpha \frac{\partial J(\theta_0,\theta_1)}{\partial\theta_1}$

优点

对于凸目标函数，可以保证全局最优；对于非凸目标函数，可以保证一个局部最优。

缺点

速度慢；数据量大时不可行；无法在线优化，处理动态产生的新样本。

1.3梯度下降的直观理解（An intuitive understanding of gradient descent ）

我们更深入研究一下，更直观地感受一下这个算法是做什么的，以及梯度下降算法的更新过程有什么意义。梯度下降算法如下：
$\theta_j:=\theta_j-\alpha\frac{\partial J(\theta)}{\partial\theta_j}$
描述：对 $\theta$赋值，使得 $J(\theta)$按梯度下降最快方向进行，一直迭代下去，最终得到局部最小值。其中 $\alpha$是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。

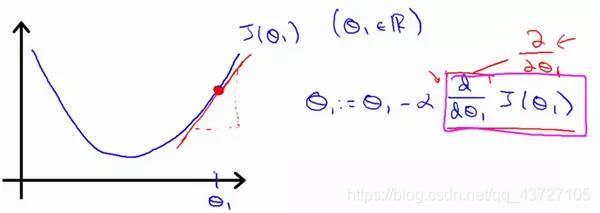
对于这个问题，求导的目的，基本上可以说取这个红点的切线，就是这样一条红色的直线，刚好与函数相切于这一点，让我们看看这条红色直线的斜率，就是这条刚好与函数曲线相切的这条直线，这条直线的斜率正好是这个三角形的高度除以这个水平长度，现在，这条线有一个正斜率，也就是说它有正导数，因此，我得到的新的 $\theta_1$， $\theta_1$更新后等于 $\theta_!$减去一个正数乘以 $\alpha$。

这就是我梯度下降法的更新规则： $\theta_j:=\theta_j-\alpha\frac{\partial J(\theta)}{\partial\theta_j}$

让我们来看看如果 $\alpha$太小或 $\alpha$太大会出现什么情况：

如果 $\alpha$太小了，即我的学习速率太小，结果就是只能这样像小宝宝一样一点点地挪动，去努力接近最低点，这样就需要很多步才能到达最低点，所以如果 $\alpha$太小的话，可能会很慢，因为它会一点点挪动，它会需要很多步才能到达全局最低点。

如果 $\alpha$太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，所以，如果 $\alpha$太大，它会导致无法收敛，甚至发散。

现在，还有一个问题，当我第一次学习这个地方时，我花了很长一段时间才理解这个问题，如果我们预先把 $\theta_1$放在一个局部的最低点，你认为下一步梯度下降法会怎样工作？

假设你将 $\theta_1$初始化在局部最低点，在这儿，它已经在一个局部的最优处或局部最低点。结果是局部最优点的导数将等于零，因为它是那条切线的斜率。这意味着你已经在局部最优点，它使得 $\theta_1$不再改变，也就是新的 $\theta_1$等于原来的 $\theta_1$，因此，如果你的参数已经处于局部最低点，那么梯度下降法更新其实什么都没做，它不会改变参数的值。这也解释了为什么即使学习速率 $\alpha$保持不变时，梯度下降也可以收敛到局部最低点。

我们来看一个例子，这是代价函数 $J(\theta)$。

我想找到它的最小值，首先初始化我的梯度下降算法，在那个品红色的点初始化，如果我更新一步梯度下降，也许它会带我到这个点，因为这个点的导数是相当陡的。现在，在这个绿色的点，如果我再更新一步，你会发现我的导数，也即斜率，是没那么陡的。随着我接近最低点，我的导数越来越接近零，所以，梯度下降一步后，新的导数会变小一点点。然后我想再梯度下降一步，在这个绿点，我自然会用一个稍微跟刚才在那个品红点时比，再小一点的一步，到了新的红色点，更接近全局最低点了，因此这点的导数会比在绿点时更小。所以，我再进行一步梯度下降时，我的导数项是更小的， $\theta_1$更新的幅度就会更小。所以随着梯度下降法的运行，你移动的幅度会自动变得越来越小，直到最终移动幅度非常小，你会发现，已经收敛到局部极小值。

回顾一下，在梯度下降算法中，当我们接近局部最低点时，梯度下降法会自动采取更小的幅度，这是因为当我们接近局部最低点时，很显然在局部最低时导数等于零，所以当我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。所以实际上没有必要再另外减小 $\alpha$。

这就是梯度下降算法，你可以用它来最小化任何代价函数 $J$，不只是线性回归中的代价函数 $J$。

1.4随机梯度下降（Stochastic Gradient Descent）

如果我们一定需要一个大规模的训练集，我们可以尝试使用随机梯度下降法来代替批量梯度下降法。

在随机梯度下降法中，我们定义代价函数为一个单一训练实例的代价：

随机梯度下降算法为：首先对训练集随机“洗牌”，然后：

Repeat (usually anywhere between1-10){

for i=1:m{

(for j=0:n)

}}

随机梯度下降算法在每一次计算之后便更新参数 $\theta$ ，而不需要首先将所有的训练集求和，在梯度下降算法还没有完成一次迭代时，随机梯度下降算法便已经走出了很远。但是这样的算法存在的问题是，不是每一步都是朝着”正确”的方向迈出的。因此算法虽然会逐渐走向全局最小值的位置，但是可能无法站到那个最小值的那一点，而是在最小值点附近徘徊。

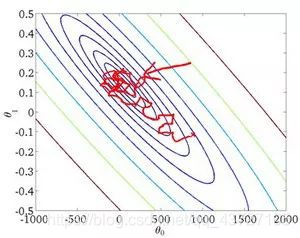
优点

更新频次快，优化速度更快; 可以在线优化(可以无法处理动态产生的新样本)；一定的随机性导致有几率跳出局部最优(随机性来自于用一个样本的梯度去代替整体样本的梯度)。

缺点

随机性可能导致收敛复杂化，即使到达最优点仍然会进行过度优化，因此SGD得优化过程相比BGD充满动荡。

1.5小批量梯度下降(Mini-batch gradient descent)

小批量梯度下降算法是介于批量梯度下降算法和随机梯度下降算法之间的算法，每计算常数b次训练实例，便更新一次参数 $\theta$。

Repeat {

for i=1:m{

? (for j=0:n )

? i+=10

} }

通常我们会令 $b$在 2-100 之间。这样做的好处在于，我们可以用向量化的方式来循环 $b$个训练实例，如果我们用的线性代数函数库比较好，能够支持平行处理，那么算法的总体表现将不受影响（与随机梯度下降相同）。

优点

参数更新时的动荡变小，收敛过程更稳定，降低收敛难度；可以利用现有的线性代数库高效的计算多个样本的梯度。

1.6优化算法

1、动量梯度下降法（Gradient descent with Momentum）

2、RMSprop algorithm(root mean square prop)

3、Adam优化算法（Adam optimization algorithm）

4、学习率衰减（Learning rate decay）
参考资料GitHub
参考GitHub