降噪变分自编码器（Denoising VAE），是将Denoising Criterion和VAE结合在一起的一种自编码器。大致来说，对输入按一个分布加入噪声，然后将扰乱后的样本作为的VAE的输入，并令VAE重构没有加入噪声的样本。
回顾VAE，对于所有样本，我们希望最大化其对数似然,即
L被称为是变分下界，最大化logp(x)
可以通过最大化变分下界实现，这里为了区分，定义为
。
在此基础上，我们对输入x加入噪声，令噪声破坏后的输入（corrupted input）为
，假设噪声的分布
是一个已知的分布（可以省去参数ψ，即变为无参分布），这里我们直接取为无参分布
，则原始VAE模型中的编码器
变为了
暂且不考虑如何优化该目标，首先需要明确一些细节：
的式子无法进一步变换为类似标准VAE的重构误差与KL散度的形式，因为期望下的分布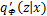
与分母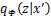
已经不是同一分布。- 根据不等式，我们得到了
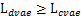，但这和
并没有必然的联系，只能说
很可能是一个比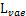
更紧的下界，但也存在反例。这主要取决于噪声的分布
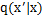，如果其噪声强度过大，导致扰乱后的样本失去了重要信息，那么势必会导致
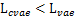。所以一个结论是，DVAE是一个对噪声分布敏感的模型。 - 我们还需要明确，最大化
的过程中，我们实际是在干什么，按照标准VAE的框架来看，我们的目标其实是在最小化近似后验和真实后验的距离，将此带入DVAE，即
如果将
换成
，这个等式会变成什么呢？这里不加证明地给出：
4. 关于等式
如果选择直接优化
也是可以的，并且只需要基于标准VAE框架上，在数据读入后，训练前加入噪声，其他不变即可。
附加的，我们可以稍微分析一下为什么DVAE很有可能比VAE效果好。直觉上说，DVAE能够对略加破坏的样本进行重构并恢复其未破坏的状态，其鲁棒性是比VAE要好的，因为其编码部分一定学到了如何排除噪声并提取重要特征的能力，但VAE由于没有人为加入噪声的干扰，所以我们不清楚其是否连带着噪声一并编码进z中。
接下来，从公式上去分析原因。我们会首先看到
也是近似标准高斯分布的，之后会结合高斯混合来最终解释。
首先对
进行变形如下：
可知，在训练过程中，是会有约束使得
近似标准高斯分布p(z)的。
接下来，观察近似后验分布
的表达式：
是一个已知的概率分布，而
又是一个近似标准高斯分布的分布，所以整体上，我们可以近似认为
是一个高斯混合模型。与VAE相比，DVAE以高斯混合模型对后验概率p(z|x)建模，而VAE则是以高斯分布对p(z|x)建模建模，显然，如果
选择的合适，VAE可以处理的DVAE也可以处理，并且VAE不能处理的（多峰）DVAE仍然可以处理。