第四章 低级特征提取 一阶边缘检测算子Sobel、Prewitt、Canny等
4.1 概述
a. 我们定义低层次特征为基本特征,不需要任何形状信息就可以从图像中自动提取;
局部特征提取:边缘检测;角点检测(线条高曲率点);局部兴趣图像块;
运动特征,常用方法为光流;
4.2 边缘检测
4.2.1 一阶边缘检测算子
4.2.1.1 基本算子
a. 基于边缘检测的分析不易受整体光照强度变化的影响,因此被用于很多图像理解环境中;边缘检测强调的是图像对比度,即亮度差异的明显性;人类视觉系统对目标的感知正是依赖于这种机制;
一阶微分可以简单地描述这种灰度起伏;
b. 离散数据一阶微分近似
水平边缘检测算子,检测水平方向的灰度差,即检测垂直的边缘;一个简单的算子形式是
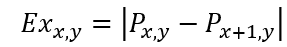
垂直边缘检测算子,检测垂直方向的灰度差;
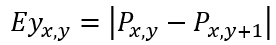
则有合并算子E,同时对垂直和水平边缘进行检测,有
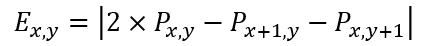
该算子给出差分模板的系数,模板可以描述为
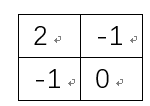
它可以与图像做卷积运算检测所有边缘点;
4.2.1.2 基础算子的分析
a. 设?x为相邻点坐标差值,f(x+?x)-f(x)即灰度差,则f’ (x)的t泰勒展开形为
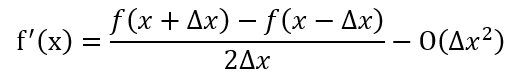
其中O(?x2 )为估算误差,一般取决于间距?x的大小和灰度曲线的复杂程度(;
b. Roberts交叉算子
卷积模板形式,
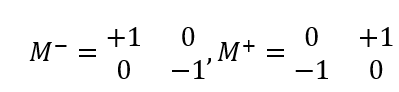
一般考虑将边缘表示为矢量成分;
4.2.1.3 Prewitt边缘检测算子
a. 易见,边缘检测算子对灰度突变进行正响应,频域模拟为高通滤波器,因此均值处理这类低通滤波预处理操作对边缘检测有一定的影响;
Prewitt算子作用是合并边缘检测和均值算子,其卷积模板为,
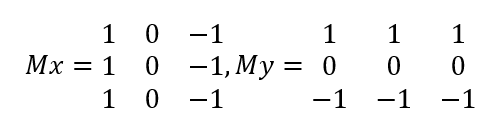
Prewitt算子给出变化率构造矢量,Mx和My的符号可以进一步确定边缘方向的相应象限;由于需要进行直接均指计算和基础一阶边缘检测,Prewitt算子不太适合简单模板;
4.2.1.4 Sobel边缘检测算子
a. Sobel算子是由以矢量方式确定边缘的两个掩码组成的,其模板构造为,
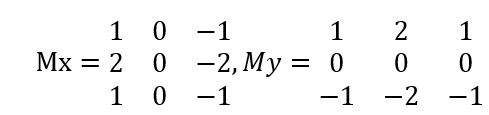
b. 可以用于计算大模板系数的理论基很少被提到,一个可能的理论基础是考虑均值计算和差分处理的最优方式;高斯平均是公认的最优均值算法;
有一些圆形边缘算子是为了得到正确的边缘方向数据而专门设计的;
Sobel模板也可以用来处理与窗口大小相同维数的矩阵,从中计算出边缘强度和梯度;
简单算子里Sobel效果拔群;
c. Sobel算子反转,影响边缘方向的计算;
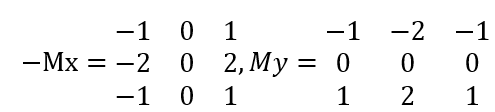
反转模板可以对Sobel算子检测到的边缘方向给出四个可能方向;这种重新排列可以简化形状检测的算法结构,利用边缘检测来找出形状的算法都必须精确地知道使用何种排列方式;
4.2.1.5 Canny边缘检测算子,当前最受欢迎的边缘检测方法
a. Canny边缘检测算子由三个主要目标形成:
无附加响应的最优检测(降低噪声);
检测边缘位置和实际边缘位置之间距离最小的正确定位(正确性,可以通过非极大值抑制实现);
减少单边缘的多重响应而得到单响应;
b. 高斯算子,
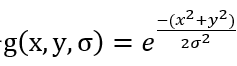
沿坐标轴对单位矢量Ux=[1,0]和Uy=[0,1]进行微分处理有,
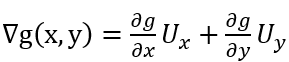
该算子结合了高斯平滑和不同方向的一阶微分;
图像经过平滑处理后,边缘由尖峰表现为数据岭的形式;为了进行更精准的定位可以在边缘法线方向上进行一阶微分,以极值作为边缘准确定位;
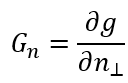
表示高斯函数g在法线n⊥的一阶导数;
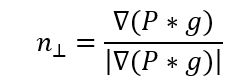
则边缘点算子,
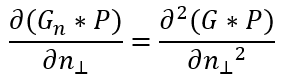
满足最小定位标准(非极大值抑制);
c. 通常采用如下近似:
(1)应用高斯平滑处理;
(2)应用Sobel算子;
(3)应用非极大值抑制;
(4)滞后阈值处理对边缘点进行连接;
d. 非极大值抑制利用边缘方向信息来处理,验证是否为峰值;
离散梯度极值的近似,
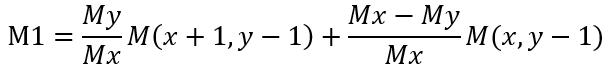
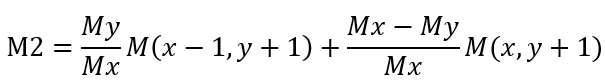
若M大于M1和M2,则保留边缘点;
e. 非极大值抑制的实现首先需要一个函数生成两点的坐标,在这两点之间插入边缘强度;
f. 滞后阈值;
滞后阈值用于对非极大值抑输出的峰值点进行处理;
滞后阈值即当当前点取高值时,如果相邻点低于阈值下限,则相邻点输出低值,否则保持高值;当前点取低值时,如果相邻点高于阈值上限,则相邻点输出高值,否则保持低值;