第四章 低级特征提取(5)SIFT特征、显著性算子、图像运动的描述
4.4.2 现代方法:区域/图像块分析
a. 局部特征提取的现代方法旨在放开早期的局部特征提取所设的一些限制,以便于拜托尺度差异对特征提取和描述带来的影响,通过利用多点排列的描述对目标进行描述和识别;该类方法一般依赖于尺度空间,兴趣特征一般为仍然存留在所选尺度上的特征;
4.4.2.1 尺度不变特征变换,SIFT
a. SIFT的目标是解决低层次特征提取及其在图像匹配应用中的很多实际问题,特别用于存在尺度变换的情况下;SIFT一般包括特征提取和描述两个步骤,特征提取选取具有尺度和旋转不变性的显著特征(降低遮挡、杂波、噪声干扰),并对低层次特征进行描述;
b. 首先把高斯算子的差值用于图像以确定一些可能的兴趣特征,该方法的目的是保证特征选取不依赖于特征尺度和朝向;其次对这些特征进行分析,再利用局部梯度方向确定特征朝向之前确定特征的位置和尺度;最后将特征集转换为某种具体的表达形式;从本质上而言,该算子是利用局部信息来优化标准算子所得到的信息;
c. SIFT描述算子的计算,首先计算图像高斯差值,
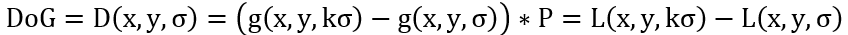
则L称为尺度空间函数,用于定义不同尺度的平滑图像;
通过将目标点与其邻域进行对比判断是否为候选点,进一步需要对低对比度候选点(泰勒展开-均一阈值处理等)和在边缘上定位不准的点进行处理(通过Harris算子等),利用局部曲线拟合函数确定局部边缘强度、稳定性、位置;
d. 不同尺度上的滤波后关键点特征描述为:

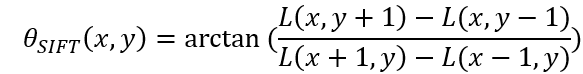
选取关键点附近的直方图峰值作为特征局部方向,计算正规朝向以得到旋转不变性和近似亮度不变性;
参考
www.cs.ubc.ca/spider/lowe/research.html
https://www.cnblogs.com/wangguchangqing/p/4853263.html
e. 生成特征描述,通过一组向量描述特征点生成特征点描述算子,主要步骤为,
(1)校正旋转方向;
(2)生成描述子,对目标点邻域的88区域,以目标点位中心分成4个44邻域像素尺寸,对每个4*4子区域-,计算每个像素的梯度幅值与梯度方向,利用高斯窗口进行加权运算得到8方向梯度直方图,计算每个标准方向的累加值形成一个种子点;
(3)对描述子进行归一化消除局部亮度等的影响;
4.4.2.2 SURF特征
a. SURF采用不同尺度的二阶边缘检测近似,通过各类二阶近似模板(如垂直二阶近似、对角二阶近似等)给出比对图像进行平滑和重采样更快地处理以形成一个在尺度空间方法中很常见的不同尺度的金字塔结构;;
利用图像亮度的泰勒展开可以得到Hessian矩阵M,则

其中L相关项同样根据高斯函数微分算子和图像得出,
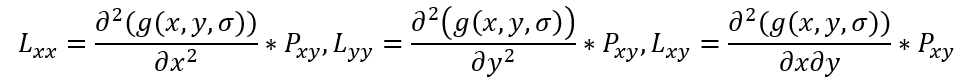
w为手动系数,作用是平衡方程各项;
b. 为了定位图像中各个尺度上的兴趣点,在333邻域采用非最大值抑制;
Hessian矩阵行列式的最大值在尺度空间和图像空间被插值,并且通过水平和垂直Harr小波得到的朝向进行描述;
4.5 运动图像描述
4.5.1 基于区域的方法
a. 对固定场景,运动目标可以看作是一组图像平面上的位移,该位移所对应的是场景中目标的投射移动,这称为光流;使用光流可以基于像素/帧对运动进行描述,对像素的运动描述同样可以推广到图像的替代特征,如点、像素、曲线、目标等;
b. 帧间对应方法有很多,可以通过特征、约束条件、优化或者检索策略等进行区分;
对像素特征可以通过局部邻域点之间的相似度找到对应点(基于区域的匹配方法,常用);一般来说,无遮挡区域的像素之间密切相关,只需要进行一般性变换
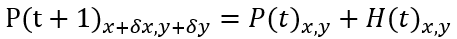
其中H(描述帧间亮度补偿,δx,δy表示帧间像素位移矢量;
对模型的简化认为帧间图像像素近似不变,且相邻像素的运动相近,则区域匹配可以描述为一个优化问题,其目的是找到使误差最小的矢量(δx,δy),
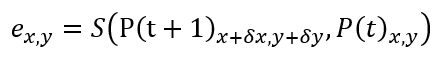
其中S为相似度度量函数,看作极大似然估计问题,则需要计算平方误差S(x)=x2((P1-P2)2);
考虑到上述上述位移是对像素的比较,容易产生误差,且存在图像整体的变化导致的像素点匹配错误,因此优化处理需要考虑邻域运动的一致性,即

通过引入一个隐式的平滑系数可以使计算更加稳定;
增大窗口W可以得到更平滑的结果,但是会模糊边界;小窗口则会导致边界噪声较大;
4.5.2 微分方法
a. 像素值的微分变化是常用的光流算法,考虑亮度均衡,认为同一像素在帧间亮度相同,当前帧像素泰勒展开有
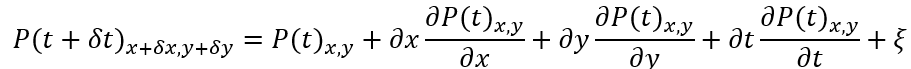
取δt=0则ξ可忽略;且有运动约束方程
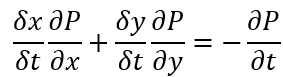
则光流有关的项表示为u=δx/δt,v=δy/δt,分别表示水平和垂直方向的光流分量;
表示为点积形式有?P?v=-P ?,其中?P=[?x ?y]=[?P/?x ?P/?y],光流v=[u v]T;
对于一组图像,?P,?t是已知的,但光流矢量v=[u v]T通常具有若干中可能的不同组合,从本质上看采取的方法是对整体图像计算误差最小的u和v的估算值,考虑到u?x+v?y+?t=0,可以得到使像素上所有像素的整体误差ec最小的估算值
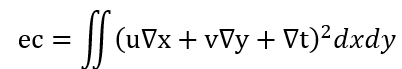
由于想要使平滑最大化,所以需要使两轴上光流变化率的积分达到最小,即认为相邻点光流不具有差异,
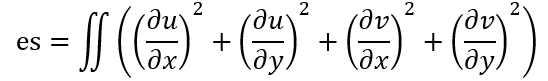
则总误差表示为不变亮度假设和平滑速度假设的折中,表示为
e=λ×ec+es
其中λ是正规化参数;
b. 假设误差的离散实现为:
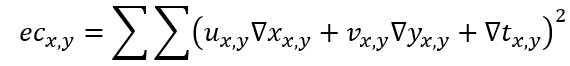

整体误差对u,v分别进行微分,
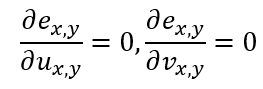
这一方程组的求解过程采用迭代形式,记u在n次迭代的估算值为u<n>,每次迭代为每个点的光流计算一对新值
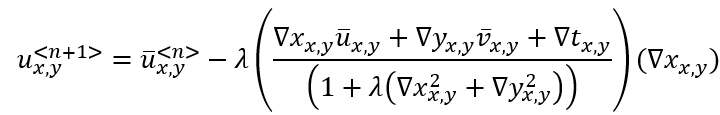
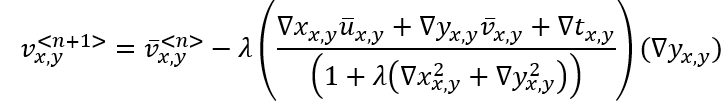
对一阶微分采用近似估算,即有
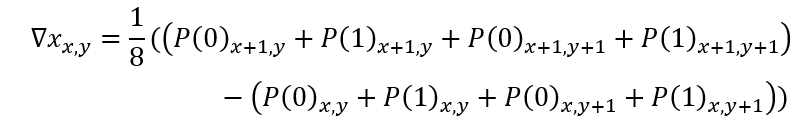
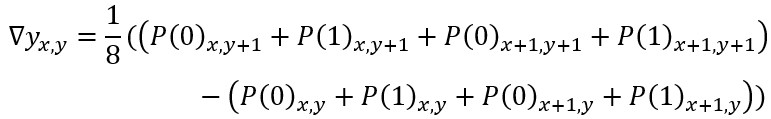
时间微分是通过这个正方体两个面上的两个像素之间的差值计算的(避免帧间定位错误),如

对于多帧间隔应该调整对应的分母(因此实际上光流幅值描述的不是对比差异,而是单位速度);又
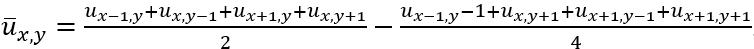
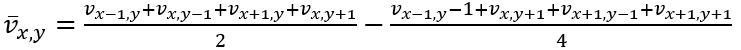
则可以解出相应的u,v最小值点对;
需要注意,离散导数近似一般只用于小位移情况,对于较大位移一般采用梯度算法;