第三十九篇 数值积分-牛顿柯特斯
当以解析法去求代数积分时不便利或者根本求不出来时,就使用数值积分或“求积”的方式。数值积分方法可以应用在数学函数,或者针对工程实验中能够测量的离散数据。首先考虑一元函数的数值积分方法,即:

多个变量函数的面积和体积积分将在后面讨论。
本篇将介绍几种数值积分公式(也称为“法则”)。这些方法通常不依赖于被积分的函数类型,但一些“自定义”方法也会被讨论。
少数情况下数值积分有时会得到精确解,特别是如果处于计算的函数是一个简单的多项式,但通常最后的解是近似的。在积分是由超越函数所组合(如正弦、余弦、对数等)成时,函数在任何情况下都可能没有精确的解析解。一旦得到了近似解,那么就需要知道误差值的大小了。在某些情况下,数值积分规则可以具有自适应的特点去求出最精确的解。
数值积分方法的第一步是用一个简单的多项式Qn?1(x) (n - 1)次替换被积分的函数f(x),它在n个点处的xi和f(x)值一样,其中i = 1,2,…,n。
因此

其中

ai是常系数。
像Qn?1(x)这样的多项式很容易解析积分,也可以精确地进行数值积分。因此,如果像上面一样可以求出一个近似的形式,可以得到一个所需积分的合理估计。
数值积分的“法则”通常表示为求和的形式

因此

xi被称为“采样点”,即函数f(x)的取值点,wi是常数“加权系数”。上面方程构成了在单一变量中所有数值积分方法的基础。
虽然Qn?1(x)实际上是由方程积分的函数,但并不需要知道它的确切形式,因为样本点将会被代入f(x)中。
两个数值积分法则的区别在于样本点的数量和位置以及对应的加权系数。
首先考虑的方法为,将样本点在积分范围内取等间隔的“牛顿科特”法则。后来得到的方法“高斯”法则,其中样本点取最优的间隔,能显著地提高精度和效率
数值积分的其他需要在本篇中处理的有采取自适应方法去控制误差、特殊的包含一个指数衰减函数或某种类型的奇点的被积函数,和多个变量的多重积分函数在二维和三维情况下。
样本点一般在积分范围内,故a≤xi≤b。
然而还将有样本点在积分范围之外的情况,这将在之后讨论。
牛顿柯特法则
牛顿柯特法则的特点是在积分范围和限制之内等间隔的取样本点。在下面的小节中,我们将描述牛顿-科特斯家族的前几个成员,从只使用一个样本点的最简单的方法开始。
矩形法则,(n=1)
这种简单的方法也被称为“矩形法则”,积分的近似函数f(x)仅与第一个点的多项式Q0(x)一致,即积分下限如下图所示。
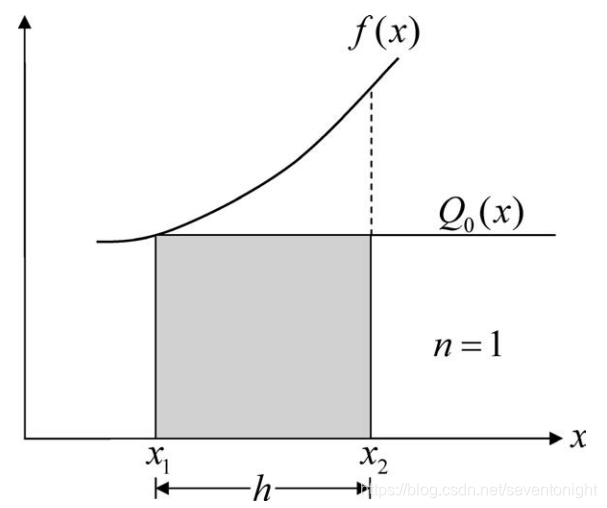
由于被积分的函数是常数,解是阴影矩形的面积,因此,矩形规则为

显然,这种方法不是特别精确,只有当f(x)本身是一个零阶多项式,即一条平行于x轴的线时,才会得到精确的解。
计算实例
使用矩形规则计算下面函数的值

解:

因此:

这种情况下的解是非常不准确的,因为在要积分的范围内,在第一个点取得函数完全没有代表性。
虽然这种方法对于常规函数不推荐使用,这种简单得方式还是有吸引力得,后面的一个求解常微分方程称为“显式”的算法就是基于此规则
梯形法则,(n=2)
这是一种很常用的方法,其中f(x)近似为一个一阶多项式Q1(x),它与f(x)在积分的 两侧重合。如下图所示,积分近似为梯形的面积。梯形法则:

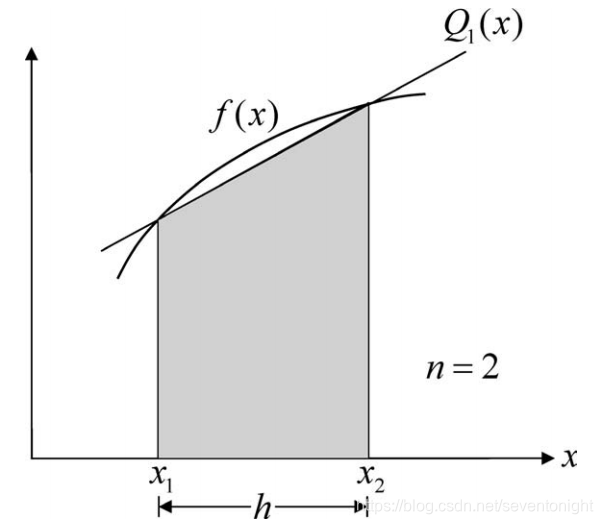
这种算法对于f(x)的次数小于等于1时是准确的。
计算实例
使用梯形法则去计算下面积分的值

解:

因此

数值解虽然比矩形规则的结果好,但仍然和正确解有差距。通过使用“重复”法则可以找到更准确的估计,下一篇将详细介绍。
辛普森(simpson)法则
另一种著名的方法是将f(x)近似为一个二阶多项式Q2(x), Q2(x)在与f(x)有三个点重合,即积分的两端和积分的中间值。然而,与前面的例子不同的是,Q2(x)的面积不能用简单的几何推导出来,因此介绍了一种高效而通用的方法来推导数值积分规则,称为“多项式代换法”。
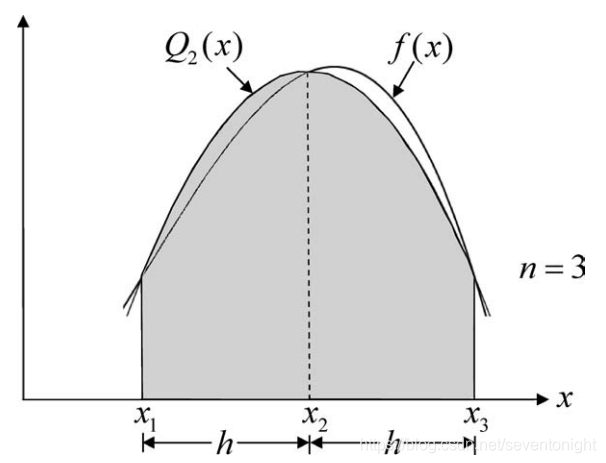
多项式替代方法
在这个例子中,我们将使用多项式替代法来推导一般形式的三点(n = 3)牛顿-柯特法则的加权系数

其中x2 = (x1 + x3)/2 x3?x2 = x2?x1 = h。
根据前两个牛顿科特法则所建立的形式,可以假定,当f(x)是一个0阶、1阶或2阶多项式时,方程中三个样本点的辛普森法则是准确的。这可以用未知的w1、w2和w3产生3个方程式。
然而,在开始推导之前,对问题做一个临时的变换,使积分范围的中点在原点,积分的上下限为±h,使得对未知数的求解更简单。为了实现上述过程,将所有的x值平移x2得到一个变换后的函数F(x),其中

和

让F(x)=1

让F(x)=x

让F(x)=x2

由上面方程得到

因此

回到原来的函数和上下限值,得到

计算实例
使用辛普森(simpson)法则计算下面的积分

解

因此

希望读者可以自己计算上面的推导过程,以验证多项式代换法的正确性。
结果证明辛普森法法则对于f(x)为3次多项式时是正确的。
高阶牛顿科特法则(n>3)
在牛顿-柯特法则中,对样本点的数量是没有限制的。四点法则可以适合于三次f(x)的积分,并且对于f(x)次数为3或者更小的情况是精确的。5点规则适用于f(x)的为四次式的积分,适用于f(x)为5次式或更小的情况,以此类推
然而,这些高阶规则在实践中很少使用,因为“重复的”低阶方法是优先选用的。
牛顿科特规则的精确性
偶数个样本点(即n = 2,4,…)可以精确地积分次数小于1的多项式(即n?1),奇数个样本点(即n = 3,5,…)的规则效率更高,这种差异的原因可以通过辛普森法则(n = 3)的图来证明,如果f(x)是三次式,它将被精确地积分,因为在近似多项式Q2(x)中上下出现的误差被抵消了。
为了更精确地评估牛顿-柯特法则的正确性,需要将该法则产生的结果与精确解写成的泰勒级数进行比较。级数中被近似解忽略的最大项称为“主要误差项”。
矩形法则的误差(n=1)
考虑f(x)关于下限x1的泰勒级数展开,即,

方程两边的积分得到

替换积分限h = x2?x1将变成

比较方程1之后,可以得出结论主导误差项为1/2h2f’ (x1)。
梯形法则的误差
再次取h = x2?x1,考虑f(x)关于积分下限x1的泰勒级数展开,得到f(x2),即

通过乘1/2h之后得到

将这个方程代入方程3后得到,

比较方程2之后得到,最大的主要误差项为-1/12h**3f’’(x1)
辛普森(simpson)法则的误差(n=3)
如果法则中多项式的最高阶数是已知的,则可以使用另一种方法来寻找主要误差项。
辛普森法则对三次幂精确积分,但只对四次幂近似积分,因此,主要误差项肯定包含四次导数,得到

令f(x) = x4

因此

所以辛普森法则的主要错误项为

牛顿科特法则的总结
所有牛顿-柯特定律都可以写成下面的形式

式中,h表示样本点之间的距离xi = a + (i?1)h, i = 1,2时系数Wi,…,n和C是一个常数。F k(x)表示F (x)的第K阶导数。上式中的值汇总在下表。
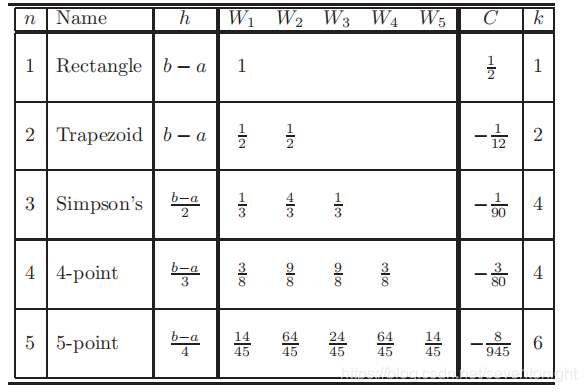
描述牛顿-柯特规则的另一种方法是考虑积分上下限为±1的正交化问题,从而便于与本篇后面将要介绍的高斯规则进行比较

在这种情况下,间隔h是已知的,因此它的数值直接包含在加权系数wi中。上面方程中的值总结了下表中,下面的表包括前5个正交化牛顿-柯特法则的样本点和权重值。
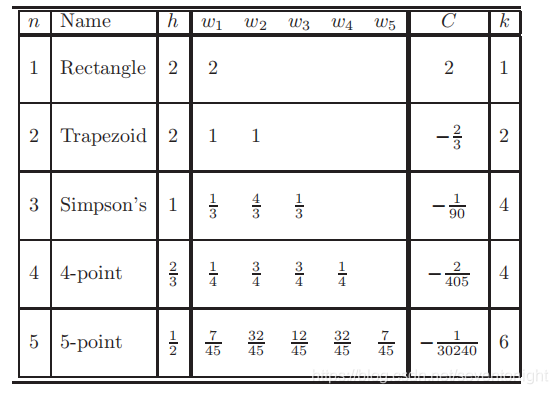

从上表可以,加权系数在积分范围的的中点两边是对称的,它们的和始终等于积分范围的值。
虽然主要误差项系数C对这些法则的准确性有很大影响,但实际的主要误差项既包括h的某次幂,也包括被积分的函数的导数。显然,当h变小时(当h < 1时),误差项也会变得很小,但对于某些函数应该注意如果具有高阶导数,值不应该太大。