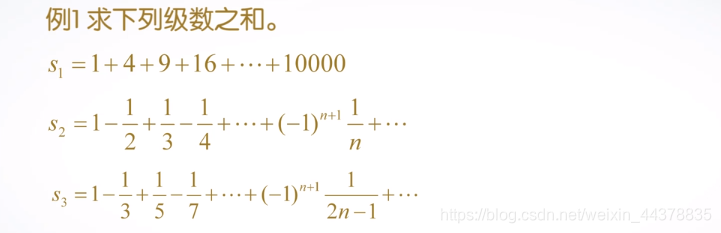7. 符号计算

A 符号对象

A.a 符号对象的建立

• sym函数
• syms命令

<1> sym函数
sym函数用于建立单个符号对象，其常用调用格式为：符号对象名=sym(A)
将由A来建立符号对象。其中，A可以是一个数值常量、数值矩阵或数值表达式（不加单引号），此时符号对象为一个符号常量；A也可以是一个变量名（加单引号），这是符号对象为一个符号常量。

例子（符号常量）：

t = sym(2);
t+1/2
sin(sym(pi/3))
sin(pi/3)

$sin(sym(pi/3))$得到的是一个表达式，而$sin(pi/3)$得到的是一个数值。
例子（符号变量)：

a = 5;
b = -8;
x = sym('a');
y = sym('b');
w = (a+b)*(a+b)
s = (x+y)*(x+y)

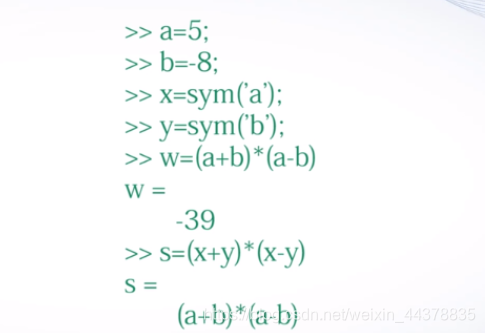
结论：符号计算的结果是一个精确的数学表达式。数值计算的结果是一个数值。

将符号表达式转化为数值结果，使用eval() 将字符串当成命令来实现

sym一次只能定义单个符号对象，如果符号对象很多，就不方便。

---

<2>syms命令
syms命令可以一次定义多个符号变量，其一般调用格式如下：
syms 符号变量1 符号变量2 ... 符号变量n
其中，变量名不能加单引号，相互之间用空格隔开。如：

建立完符号对象，再用符号运算符连接起来，就组成了符号表达式。

A.b 符号对象的运算

<1>四则运算
符号表达式的四则运算与数值运算一样，用+、-、*、/运算符实现，其运算结果依然是一个符号表达式。

syms x;
f = 2*x^2+3*x-5;
g = x^2-x+7;
f+g

<2>关系运算

• 6种关系运算符：<、<=、>、>=、==、~=。
• 对应的6个函数：lt()、le()、gt()、ge()、ge()、eq()、ne()。

若参与运算的是符号表达式，其结果是一个符号关系表达式；若参与运算的是符号矩阵，其结果是由符号关系表达式组成的矩阵。

在进行符号对象的运算前，可用assume函数对符号对象设置域，函数调用格式为：
assume(condition)
assume(expr, set)

第一种格式指定变量满足条件condition，第二种格式指定表达式expr属于set

<3>逻辑运算

• 3种逻辑运算符：&(与)、|(或)和~(非)
• 4个逻辑运算函数：and()、or()、not()和xor()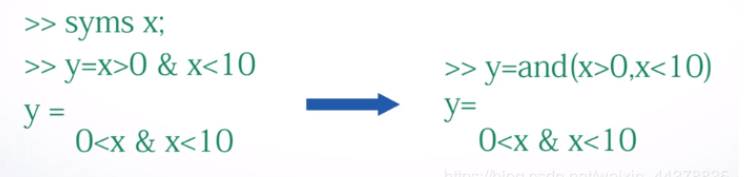
• 

<4>因式分解与展开运算
MATLAB提供了对符号表达式进行因式分解、展开、合并的函数，函数的调用格式为：
fator(s)：对符号表达式s分解因式。

syms a b;
s = a^3-b^3;
factor(s)

%梅森素数
syms p;
m = 2^p-1;
p = 19;
m19 = eval(m)
factor(m19)

expand(s)：对符号表达式s进行展开。
collect(s)：对符号表达式s合并同类项。
collect(s, v)：对符号表达式s按变量v合并同类项。

<5>其他计算

• 1 提取有理分式的分子分母：[n, d]=numden(s)
  
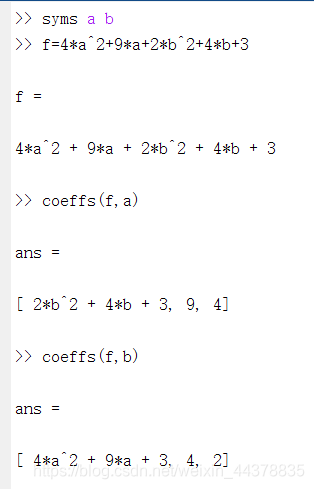
• 2 提取符号表达式的系数(低位到高位)：c=coeffs(s, x)
  
• 3 符号表达式化简：simplify(s)
• 4符号多项式与多项式系数向量之间的转换：
  符号多项式转换为多项式系数向量：p=sym2poly(s)
  多项式系数向量转换为符号多项式：s=ploy2sym()
  
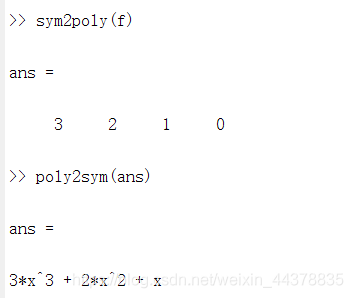
  f只能有一种符号变量

例子：

syms a b c x;
f = a*x^2+b*x+c
g = coeffs(f,x)
g = g(end:-1:1)
roots(g)

<6>符号运算中变量的确定

• 如果没有明确指定自变量，MATLAB将按以下原则确定主变量并对其进行相应运算：
  寻找除了i、j之外，在字母顺序上最接近x的小写字母。
  若表达式中有两个符号变量与x的距离相等，则ASCII码大者优先。

• symvar()函数可以用于查找一个符号表达式中的符号变量，函数的调用格式为：symvar(s,n)。函数返回符号符号表达式s中的n个符号变量。因此，可以用symvar(s, 1)查找表达式s的主变量。

A.c 符号矩阵

符号矩阵也是一种符号表达式，所以符号表达式运算都可以在矩阵意义下进行。
注意：这些函数作用于符号矩阵时，是分别作用于矩阵的每一个元素。

由于符号矩阵也是矩阵，所以有关矩阵的函数也可以使用。

syms lambda;
A = [1-lambda,-2,4;2,3-lambda,1;1,1,1-lambda];
D = det(A);
factor(D)

B 符号微积分

B.a 符号函数的极限

<1>符号函数的极限

• 求符号函数极限的命令limit，其调用格式为：limit(f, X, a)即求函数f关于变量x在a点的极限。若x省略，则采用系统默认的自变量。a的默认值为0。
• limit函数的另一种功能是求单边极限，其调用格式为：
  limit(f, x, a, 'right')
limit(f,x,a,'left')

syms a m x n;
f = (x^(1/m)-a^(1/m))/(x-a);
limit(f,x,a)
g = (1+1/n)^n;
limit(g,n,inf)

B.b 符号函数的导数

MATLAB中的求导函数为：diff(f, x, n)
即求函数f关于变量x的n阶导数。参数x的用法同求极限函数limit，可以缺省，默认值与limit相同，n的默认值是1。

syms x y;
f = sqrt(1+exp(x));
diff(f)g = x*exp(y)/y^2;
diff(g,x)
diff(g,y)

极限、导数、微分的概念是紧密关联的。有极限是可导的前提，而导数是微分之商，因此导数也称为微商。

B.c 符号函数的积分

<1>不定积分

在MATLAB中，求不定积分的函数是int，其常用调用格式为：int(f, x)求函数f对变量x的不定积分。

syms x t;
f = (3-x^2)^3;
int(f)
g = 5*x*t/(1+x^2);
int(g,t)

<2>定积分
在MATLAB中，定积分的计算也使用int命令，但调用格式有区别：
int(f, a, b)
其中，a、b分别表示定积分的下限和上限。

• 当函数关于变量x在闭区间[a, b]可积时，函数返回一个定积分的结果。
• 当a、b中有一个是inf时，函数返回一个广义积分。
• 当a、b中有一个是符号表达式时，函数返回一个符号函数。

syms x t;
int(abs(1-x),1,2)
int(1/(1+x^2),-inf,inf)
int(4*x/t,t,2,sin(x))

B.d 河道水流量的估算问题

根据实际测量，得到河流某处宽600m，其横截面不同位置某一时刻的水深如下表所示。

x	0	50	100	150	200	250	300	350	400	450	500	550	600
h（x）	4.4	4.5	4.6	4.8	4.9	5.1	5.4	5.2	5.5	5.2	4.9	4.8	4.7

①若此刻水流的流速为0.6m/s，试估计该河流此刻的流量。
②已知x方向[50,60]区间为坡式护岸的下部护脚部分，根据相关堤防设计规范，抛石护岸护脚坡度应缓于1：1.5（正切值），请估计水流冲刷是否已破坏该区域的护脚。

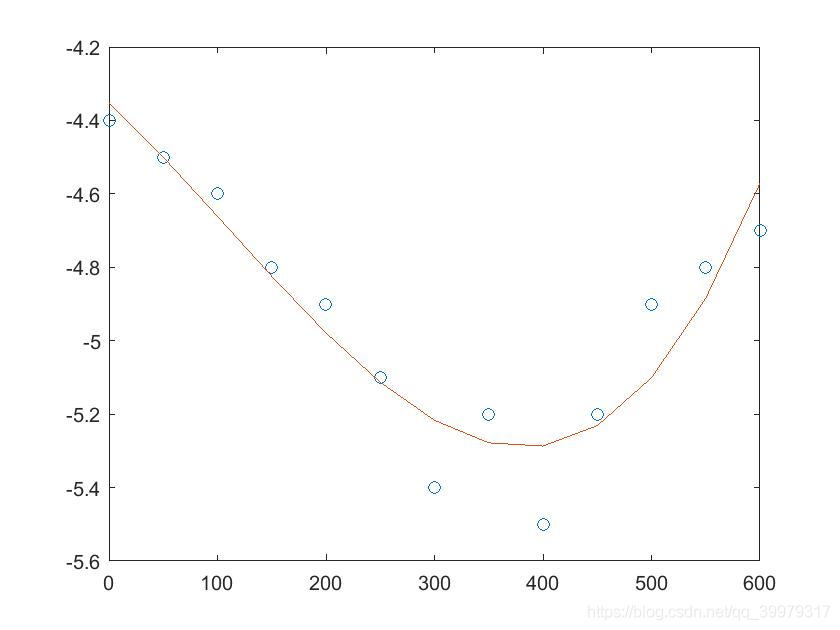
①先拟合出河床曲线，然后进行定积分，计算出河流横截面，即可估计流量。
②根据河床曲线，计算其导函数，并判断相应范围内导函数的取值是否大于1：1.5。

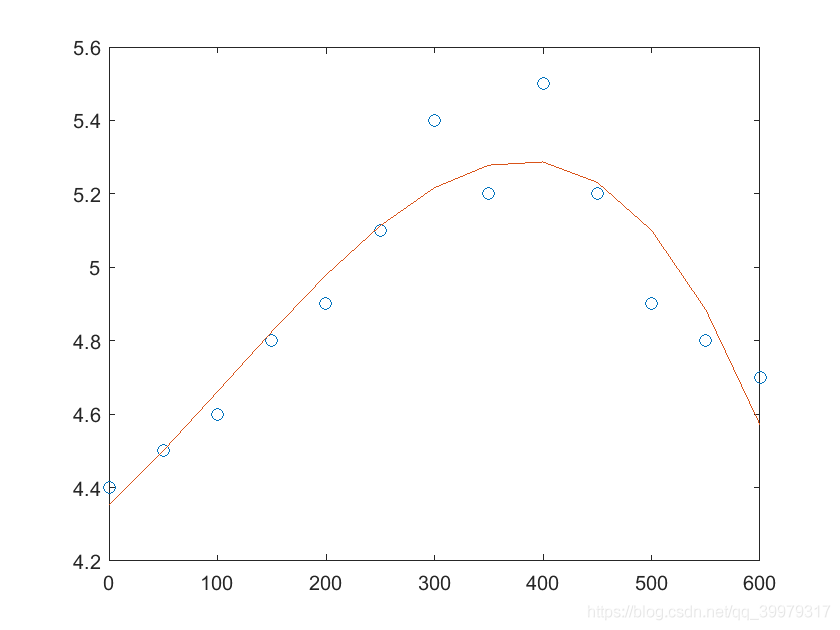
xi=0:50:600; 
yi=[4.4,4.5,4.6,4.8,4.9,5.1,5.4,5.2,5.5,5.2,4.9,4.8,4.7]; 
%曲线拟合
p=polyfit(xi, yi,3); 
plot(xi, yi,'o', xi, polyval(p, xi)); %同时画出散点图与拟合函数。
syms y x; 
y=poly2sym(p,x); 
s=int(y,x,0,600); %计算横截面积
v=s*0.6; %计算水流量
eval(v)
123456789
ans =1.7874e+03
12

方法一：

xi=0:50:600; 
yi=[4.4,4.5,4.6,4.8,4.9,5.1,5.4,5.2,5.5,5.2,4.9,4.8,4.7]; 
yn=-yi;
p=polyfit(xi, yn,3); %这两句是为了让函数开口朝上，更符合河道真实情况。
plot(xi, yn,'o', xi, polyval(p, xi)); 
syms y x yii; 
y=poly2sym(p,x); 
yii=diff(y,x); 
x=50:60; 
k=eval(yii); 
all(abs(k)<1/1.5)%判断相应范围内导函数的取值是否小于1：1.5。all（i）：若向量i中所有元素非零，结果为1，否则结果为0。
1234567891011
ans =logical1
123

方法二：

xi=0:50:600; 
yi=[4.4,4.5,4.6,4.8,4.9,5.1,5.4,5.2,5.5,5.2,4.9,4.8,4.7]; 
yn=-yi;
p=polyfit(xi, yn,3); %这两句是为了让函数开口朝上，更符合河道真实情况。
plot(xi, yn,'o', xi, polyval(p, xi)); %polyval(p, xi)可以求得多项式在xi的函数值并放到p中。
x=50:60; %步长为1
y=polyval(p,x); 
k=diff(y)/1;%diff为差分函数，步长为1，k就是微商，导数。
all(abs(k)<1/1.5) 
123456789
ans =logical1
123

可以看出，结果为1，也就是说，在[50,60]内,导函数的取值是小于1：1.5，符合要求。

C 级数

C.a 级数求和

例子：

syms n;
s1 = symsum(n^2,1,100)
s2 = symsum((-1)^(n-1)/n,1,inf)
s3 = symsum((-1)^(n-1)/(2*n-1),n,1,inf)

hypergeom:超几何函数

C.b 级数求和应用实例

假设某人在银行存款50000元，年利率为4.5%，按复利计息。
①若半年期计息一次，请问一年后总金额是多少？
②若每季度计息一次，请问一年后总金额是多少？
③若每月计息一次，请问一年后总金额是多少？
④若计息时间无限短，即计息期数趋于无穷，则一年后总金额是多少？
思考：期数无限多，总金额是否也会无限增长？
问题分析：
假 设 存 款 （ 初 始 总 金 额 ） 为 p ， 年 利 率 为 r ， 计 息 期 数 为 k 。 第 一 期 后 总 金 额 为 p ? （ 1 + r / k ） 。 第 二 期 后 总 金 额 为 p ? （ 1 + r / k ） ^2 。 第 三 期 后 总 金 额 为 p ? （ 1 + r / k ）^ 3 。 依 此 类 推 ， 第 k 期 后 总 金 额 为 p ? （ 1 + r / k ）^ k 。

①若半年期计息一次，请问一年后总金额是多少？

syms k r; 
p2=symsum(50000*(1+0.045/k)^k,k,2,2); 
eval(p2)
123
ans =5.2275e+04
12

②若每季度计息一次，请问一年后总金额是多少？

syms k r; 
p4=symsum(50000*(1+0.045/k)^k,k,4,4); 
eval(p4)
123
ans =5.2288e+04
12

③若每月计息一次，请问一年后总金额是多少？

syms k r; 
p12=symsum(50000*(1+0.045/k)^k,k,12,12); 
eval(p12)
123
ans =5.2297e+04
12

④若计息时间无限短，即计息期数趋于无穷，则一年后总金额是多少？

limit((1+r/k)^k,k,inf)%计算一下lim(1+r/k)^k,k趋于无穷大时的结果。
1
ans =
exp(r)
12

所以，即使是无数次计息，只要年利率确定，总金额也不会无限增长，它收敛于p e r pe^rper。
当p=5000,r=4.5%时。

5000*exp(0.045)
1
ans =5.2301e+03
12

C.b 特例

注 意 ： 在 符 号 计 算 中 ， 因 为 小 数 都 表 示 为 有 理 分 数 的 形 式 , 随 着 计 算 次 数 的 增 加 ， 容 易 导 致 分 子 或 分 母 出 现 极 大 整 数 从 而 无 法 计 算 的 情 况 。 \color{red}注意：\在符号计算中，因为小数都表示为有理分数的形式,随着计算次数的增加，\容易导致分子或分母出现极大整数从而无法计算的情况。注意：在符号计算中，因为小数都表示为有理分数的形式,随着计算次数的增加，容易导致分子或分母出现极大整数从而无法计算的情况。
求以下级数之和
(1) S 1 = 1 + 1 / 4 + 1 / 9 + . . . + 1 / n 2 + . . .
(2) S 2 = 1 + 1 / 4 + 1 / 9 + . . . + 1 / 500 2

syms n; 
s1=symsum(1/n^2,n,1,inf)
12
s1 = 
pi^2/6
12
syms n; 
s2=symsum(1/n^2,n,1,500)
12
s2 =
409896675094...
12
eval(s2)
1
ans =NaN
12

第2个级数无法使用symsum函数求和。但可以使用循环计算。

s=0
for i=1:500s=s+1/i^2
end
1234
s =1.6429

C.c 泰勒级数

例子：

syms x;
f = (1+x+x^2)/(1-x+x^2);
taylor(f,x,1,'Order',6)
expand(ans)

C.d 泰勒级数的应用

复杂函数的计算方法问题
除 了 四 则 运 算 以 外 ， 计 算 机 对 其 他 复 杂 函 数 怎 么 计 算 ？ 是 否 存 在 一 种 方 法 ， 使 得 计 算 机 只 需 要 通 过 四 则 运 算 ， 就 能 计 算 其 他 复 杂 函 数 ？
泰勒级数展开就是一种非常好的解决方案。
例 利用泰勒展开式计算三角函数的值。

syms x; 
f=taylor(cos(x),x,pi)%求cos(x)的泰勒展开式并赋值给f
12
f = 
(x - pi)^2/2 - (x - pi)^4/24 - 1
12
syms x; 
f=taylor(cos(x),x,pi);
x=3;
eval(f)
1234
ans =-0.9900
12
cos(3)
1
ans =-0.9900
123

通过泰勒级数展开的方法，成功地将三角函数的计算转换成了四则运算。
是不是感觉数学实在是太美妙了。

D 符号方程求解

D.a 代数方程

例子：

syms x y a b c
%法一
solve(a*x^2+b*x+c==0)%法二
f = a*x^2+b*x+c==0
solve(f)%法三
solve(a*x^2+b*x+c)%法四
f = a*x^2+b*x+c
solve(f)

solve所得到的结果可能不准确：

syms x y;
u = solve(x + (2-x^(1/3))^3==98)
v = 98-u

D.b 常微分方程

syms x y t;
y = dsolve('Dy-(x^2+y^2)/x^2/2',x)
[x,y] = dsolve('Dx = 4*x-2*y','Dy = 2*x - y',t)

注意单引号。

---

D.c 疾病传染问题

syms a b c y t;
f = dsolve('Dy = a*y*(1-y)-c*y','y(0)=b',t)f = dsolve('Dy = a*y*(1-y)-a*y','y(0)=b',t)f =((a - c)*(tanh((t + (2*atanh((2*a*b)/(a - c) - 1))/(a - c))*(a/2 - c/2)) + 1))/(2*a)f =b/(a*b*t + 1)