【机器学习】组合算法 Bootstraping, Bagging, Boosting, AdaBoost, RandomForest, Gradient boosting

组合模型

Bootstraping

名字来自成语“pull up by your own bootstraps”，意思就是依靠你自己的资源，称为自助法，它是一种有放回的抽样方法，它是非参数统计中一种重要的估计统计量方差进而进行区间估计的统计方法。其核心思想和基本步骤如下：

采用重抽样技术从原始样本中抽取一定数量（自定义）的样本，此过程允许重复抽样。
根据抽出的样本计算给定的统计量T。
重复上述N次（一般大于1000），得到N个统计量T。
计算上述N个统计量T的样本方差，得到统计量的方差。

Bootstrap是现代统计学较为流行的一种统计方法，小样本时效果很好。通过方差的估计可以构造置信区间等，其运用范围得到进一步延伸。

bagging

装袋算法相当于多个专家投票表决，对于多次测试，每个样本返回的是多次预测结果较多的那个。算法描述：

模型生成令n为训练数据的实例数量对于t次循环中的每一次从训练数据中采样n个实例将学习应用于所采样本保存结果模型
分类对于t个模型的每一个使用模型对实例进行预测返回被预测次数最多的一个

bagging：bootstrap aggregating的缩写。让该学习算法训练多轮，每轮的训练集由从初始的训练集中随机取出的n个训练样本组成，某个初始训练样本在某轮训练集中可以出现多次或根本不出现，训练之后可得到一个预测函数序列

h1，??hnh1，??hn

最终的预测函数H对分类问题采用投票方式，对回归问题采用简单平均方法对新示例进行判别。

[训练R个分类器f_i，分类器之间其他相同就是参数不同。其中f_i是通过从训练集合中(N篇文档)随机取(取后放回)N次文档构成的训练集合训练得到的。对于新文档d，用这R个分类器去分类，得到的最多的那个类别作为d的最终类别。]

使用scikit-learn测试bagging方法

from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier
bagging = BaggingClassifier(KNeighborsClassifier(),max_samples=0.5, max_features=0.5)

Boosting与Adaboost

提升算法描述

模型生成赋予每个训练实例相同的权值t次循环中的每一次：将学习算法应用于加了权的数据集上并保存结果模型计算模型在加了权的数据上的误差e并保存这个误差结果e等于0或者大于等于0.5：终止模型对于数据集中的每个实例：如果模型将实例正确分类将实例的权值乘以e/(1-e)将所有的实例权重进行正常化
分类赋予所有类权重为0对于t（或小于t）个模型中的每一个：给模型预测的类加权 -log(e/(1-e))返回权重最高的类

这个模型提供了一种巧妙的方法生成一系列互补型的专家。

boosting: 其中主要的是AdaBoost（Adaptive boosting，自适应boosting）。初始化时对每一个训练例赋相等的权重1／N，然后用该学算法对训练集训练t轮，每次训练后，对训练失败的训练例赋以较大的权重，也就是让学习算法在后续的学习中集中对比较难的训练例进行学习，从而得到一个预测函数序列h1,?,hmh1,?,hm , 其中h_i也有一定的权重，预测效果好的预测函数权重较大，反之较小。最终的预测函数H对分类问题采用有权重的投票方式，对回归问题采用加权平均的方法对新示例进行判别。

提升算法理想状态是这些模型对于其他模型来说是一个补充，每个模型是这个领域的一个专家，而其他模型在这部分却不能表现很好，就像执行官一样要寻觅那些技能和经验互补的顾问，而不是重复的。这与装袋算法有所区分。

Adaboost算法描述

模型生成训练数据中的每个样本，并赋予一个权重，构成权重向量D，初始值为1/Nt次循环中的每一次：在训练数据上训练弱分类器并计算分类器的错误率e如果e等于0或者大于等于用户指定的阈值：终止模型，break重新调整每个样本的权重，其中alpha=0.5*ln((1-e)/e)对权重向量D进行更新，正确分类的样本的权重降低而错误分类的样本权重值升高对于数据集中的每个样例：如果某个样本正确分类：权重改为D^(t+1)_i = D^(t)_i * e^(-a)/Sum(D)如果某个样本错误分类：权重改为D^(t+1)_i = D^(t)_i * e^(a)/Sum(D)
分类赋予所有类权重为0对于t（或小于t）个模型（基分类器）中的每一个：给模型预测的类加权 -log(e/(1-e))返回权重最高的类

（类似Bagging方法，但是训练是串行进行的，第k个分类器训练时关注对前k-1分类器中错分的文档，即不是随机取，而是加大取这些文档的概率。)

AdaBoosting的基本思想

通俗地讲就是综合某些专家的判断，往往要比一个专家单独的判断要好（三个臭皮匠顶过诸葛亮-周志华《机器学习第八章》）。在”强可学习”和”弱可学习”的概念上来说就是我们通过对多个弱可学习的算法进行”组合提升或者说是强化”得到一个性能赶超强可学习算法的算法。

Boosting的思路

1.找到一个弱分类器，分类器简单，快捷，易操作(如果它本身就很复杂，而且效果还不错，那么进行提升无疑是锦上添花，增加复杂度，甚至上性能并没有得到提升，具体情况具体而论)。

2.迭代寻找N个最优的分类器(最优的分类器，就是说这N个分类器分别是每一轮迭代中分类误差最小的分类器，并且这N个分类器组合之后是分类效果最优的。)。

在迭代求解最优的过程中我们需要不断地修改数据的权重(AdaBoost中是每一轮迭代得到一个分类结果与正确分类作比较，修改那些错误分类数据的权重，减小正确分类数据的权重 ),后一个分类器根据前一个分类器的结果修改权重在进行分类，因此可以看出，迭代的过程中分类器的效果越来越好，所以需要给每个分类器赋予不同的权重。最终我们得到了N个分类器和每个分类器的权重，那么最终的分类器也得到了。

归纳算法流程

输入：训练数据集M*N(M为样本数量，N为特征数量)弱，其中xi表示数据i[数据i为N维],yi表示数据的分类为yi,Y={-1,1}表示xi在某种规则约束下的分类。

输出：最终的分类器G(x)

1. 初始化训练集的权值均匀分布(每个样本数据权重均等)，

        D1 = (W11,W12,W13,...,W1M), W1i=1/M, ,M表示数据的个数，i=1,2,3…M。　

2. j=1,2,3,…,J(表示迭代的次数/或者最终分类器的个数,取决于是否能够使分类误差为0)。

（a）使用具有权值分布Dj的训练数据集学习，得到基本的分类器:Gj(x)；

（b） 计算Gj(x)在训练集上的分类误差率

求的是分错类别的数据的权重值和,表示第i个数据的权重Dj[i]；

（c）计算Gj(x)第j个分类器的系数,,ej表示的是分类错误率。

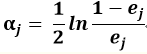
（d）更新训练数据集的权重Dj+1,数据集的权重根据上一次权重进行更新， i=1,2,…M

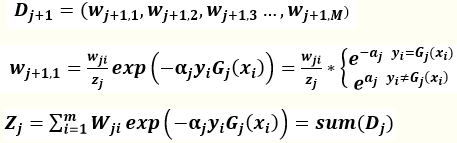
Z是规范化因子，他表示所有数据权重之和，它使Dj+1成为一个概率分布。

3. 构建基本分类器的线性组合

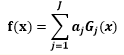
得到最终的分类器：

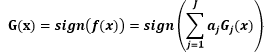
Boosting与Bagging对比：

AdaBoost泛化错误率低，易编码，可以应用在大部分分类器上，无参数调整，但是对离群点敏感。

Bagging基于数据随机重抽样的分类器构建方法，原始数据集中重新选择S次得到S个新数据集，将磨沟算法分别作用于这个数据集,最后进行投票，选择投票最多的类别作为分类类别。

Boosting关注那些已有分类器错分的数据来获得新的分类器，Bagging则是根据已训练的分类器的性能来训练的。Boosting分类器权重不相等，权重对应与上一轮迭代成功度Bagging分类器权重相等。

来源：《机器学习实战》

# -*- coding:utf-8 -*-   
from pprint import pprint  
import numpy as np  class Adaboosting(object):  def loadSimpData(self):  datMat = np.matrix([[1., 2.1],  [2., 1.1], [1.3, 1.],  [1., 1.], [2., 1.]])  classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]  return datMat, classLabels  def stumpClassify(self, datMat, dimen, threshVal, threshIneq):  # print( "-----data-----")  # print( datMat)  retArr = np.ones((np.shape(datMat)[0], 1))  if threshIneq == 'lt':  retArr[datMat[:, dimen] <= threshVal] = -1.0  # 小于阈值的列都为-1  else:  retArr[datMat[:, dimen] > threshVal] = -1.0  # 大于阈值的列都为-1  # print( "---------retArr------------")  # print( retArr)  return retArr  ''''' 单层决策树生成函数 '''  def buildStump(self, dataArr, classLables, D):  dataMatrix = np.mat(dataArr)  lableMat = np.mat(classLables).T  m, n = np.shape(dataMatrix)  numSteps = 10.0  # 步数，影响的是迭代次数，步长  bestStump = {}  # 存储分类器的信息  bestClassEst = np.mat(np.zeros((m, 1)))  # 最好的分类器  minError = np.inf  # 迭代寻找最小错误率  for i in range(n):  # 求出每一列数据的最大最小值计算步长  rangeMin = dataMatrix[:, i].min()  rangeMax = dataMatrix[:, i].max()  stepSize = (rangeMax - rangeMin) / numSteps  # j唯一的作用用步数去生成阈值，从最小值大最大值都与数据比较一边了一遍  for j in range(-1, int(numSteps) + 1):  threshVal = rangeMin + float(j) * stepSize  # 阈值  for inequal in ['lt', 'gt']:  predictedVals = self.stumpClassify(dataMatrix, i, threshVal, inequal)  errArr = np.mat(np.ones((m, 1)))  errArr[predictedVals == lableMat] = 0  # 为1的 表示i分错的  weightedError = D.T * errArr  # 分错的个数*权重(开始权重=1/M行)  print("split: dim %d, thresh %.2f, thresh ineqal:\  %s,the weighted error is %.3f" % (i, threshVal, inequal, weightedError))  if weightedError < minError:  # 寻找最小的加权错误率然后保存当前的信息  minError = weightedError  bestClassEst = predictedVals.copy()  # 分类结果  bestStump['dim'] = i  bestStump['thresh'] = threshVal  bestStump['ineq'] = inequal  # print( bestStump)  # print( minError)  # print( bestClassEst)  # 类别估计  return bestStump, minError, bestClassEst  """ 基于单层决策树的AdaBoosting训练过程： """  def adaBoostingDs(self, dataArr, classLables, numIt=40):  weakClassArr = []  # 最佳决策树数组  m = np.shape(dataArr)[0]  D = np.mat(np.ones((m, 1)) / m)  aggClassEst = np.mat(np.zeros((m, 1)))  for i in range(numIt):  bestStump, minError, bestClassEst = self.buildStump(dataArr, classLables, D)  print("bestStump:", bestStump)  print("D:", D.T)  alpha = float(0.5 * np.log((1.0 - minError) / max(minError, 1e-16)))  bestStump['alpha'] = alpha  weakClassArr.append(bestStump)  print("alpha:", alpha)  print("classEst:", bestClassEst.T)  # 类别估计  expon = np.multiply(-1 * alpha * np.mat(classLables).T, bestClassEst)  D = np.multiply(D, np.exp(expon))  D = D / D.sum()  aggClassEst += alpha * bestClassEst  print("aggClassEst ；", aggClassEst.T)  # 累加错误率  aggErrors = np.multiply(np.sign(aggClassEst) !=  np.mat(classLables).T, np.ones((m, 1)))  # 错误率平均值  errorsRate = aggErrors.sum() / m  print("total error:", errorsRate, "\n")  if errorsRate == 0.0:  break  print("weakClassArr:", weakClassArr)  return weakClassArr  """ 预测分类： datToClass：待分类数据 classifierArr: 训练好的分类器数组 """  def adClassify(self, datToClass, classifierArr):  dataMatrix = np.mat(datToClass)  m = np.shape(dataMatrix)[0]  aggClassEst = np.mat(np.zeros((m, 1)))  print('')  for i in range(len(classifierArr)):  # 有多少个分类器迭代多少次  # 调用第一个分类器进行分类  classEst = self.stumpClassify(dataMatrix,  classifierArr[i]['dim'],  classifierArr[i]['thresh'],  classifierArr[i]['ineq'])  # alpha 表示每个分类器的权重，  pprint(classEst)  aggClassEst += classifierArr[i]['alpha'] * classEst  pprint(aggClassEst)  return np.sign(aggClassEst)  if __name__ == "__main__":  adaboosting = Adaboosting()  D = np.mat(np.ones((5, 1)) / 5)  dataMat, lableMat = adaboosting.loadSimpData()  # 训练分类器  classifierArr = adaboosting.adaBoostingDs(dataMat, lableMat, 40)  # 预测数据  result = adaboosting.adClassify([0, 0], classifierArr)  pprint(result)  

bagging与boosting的区别：

二者的主要区别是取样方式不同。bagging采用均匀取样，而Boosting根据错误率来取样，因此boosting的分类精度要优于Bagging。bagging的训练集的选择是随机的，各轮训练集之间相互独立，而boostlng的各轮训练集的选择与前面各轮的学习结果有关；bagging的各个预测函数没有权重，而boosting是有权重的；bagging的各个预测函数可以并行生成，而boosting的各个预测函数只能顺序生成。对于象神经网络这样极为耗时的学习方法。bagging可通过并行训练节省大量时间开销。

bagging和boosting都可以有效地提高分类的准确性。在大多数数据集中，boosting的准确性比bagging高。在有些数据集中，boosting会引起退化— Overfit。

Boosting思想的一种改进型AdaBoost方法在邮件过滤、文本分类方面都有很好的性能。

Gradient boosting（又叫Mart, Treenet)：Boosting是一种思想，Gradient Boosting是一种实现Boosting的方法，它主要的思想是，每一次建立模型是在之前建立模型损失函数的梯度下降方向。损失函数(loss function)描述的是模型的不靠谱程度，损失函数越大，则说明模型越容易出错。如果我们的模型能够让损失函数持续的下降，则说明我们的模型在不停的改进，而最好的方式就是让损失函数在其梯度（Gradient)的方向上下降。

使用scikit-learn测试adaboost算法

1
2
3
4
5
6
7
8

>>> from sklearn.cross_validation import cross_val_score
>>> from sklearn.datasets import load_iris
>>> from sklearn.ensemble import AdaBoostClassifier
>>> iris = load_iris()
>>> clf = AdaBoostClassifier(n_estimators=100)
>>> scores = cross_val_score(clf, iris.data, iris.target)
>>> scores.mean()                             
0.9...

4.Random Forest

Random Forest： 随机森林，顾名思义，是用随机的方式建立一个森林，森林里面有很多的决策树组成，随机森林的每一棵决策树之间是没有关联的。在得到森林之后，当有一个新的输入样本进入的时候，就让森林中的每一棵决策树分别进行一下判断，看看这个样本应该属于哪一类（对于分类算法），然后看看哪一类被选择最多，就预测这个样本为那一类。 在建立每一棵决策树的过程中，有两点需要注意——采样与完全分裂。首先是两个随机采样的过程，random forest对输入的数据要进行行和列的采样。对于行采样，采用有放回的方式，也就是在采样得到的样本集合中，可能有重复的样本。假设输入样本为N个，那么采样的样本也为N个。这样使得在训练的时候，每一棵树的输入样本都不是全部的样本，使得相对不容易出现over-fitting。然后进行列采样，从M个feature中，选择m个(m << M)。之后就是对采样之后的数据使用完全分裂的方式建立出决策树，这样决策树的某一个叶子节点要么是无法继续分裂的，要么里面的所有样本的都是指向的同一个分类。一般很多的决策树算法都一个重要的步骤——剪枝，但随机森林不这样做，由于之前的两个随机采样的过程保证了随机性，所以就算不剪枝，也不会出现over-fitting。 按这种算法得到的随机森林中的每一棵都是很弱的，但是大家组合起来就很厉害了。可以这样比喻随机森林算法：每一棵决策树就是一个精通于某一个窄领域的专家（因为我们从M个feature中选择m让每一棵决策树进行学习），这样在随机森林中就有了很多个精通不同领域的专家，对一个新的问题（新的输入数据），可以用不同的角度去看待它，最终由各个专家，投票得到结果。

Random forest与bagging的区别：

(1)Random forest是选与输入样本的数目相同多的次数（可能一个样本会被选取多次，同时也会造成一些样本不会被选取到），而bagging一般选取比输入样本的数目少的样本；
(2)bagging是用全部特征来得到分类器，而Random forest是需要从全部特征中选取其中的一部分来训练得到分类器； 一般Random forest效果比bagging效果好！

使用scikit-learn测试随机森林算法

from sklearn.ensemble import RandomForestClassifier
X = [[0, 0], [1, 1]]
Y = [0, 1]
clf = RandomForestClassifier(n_estimators=10)
clf = clf.fit(X, Y)

5.Gradient boosting

梯度提升树或者梯度提升回归树(GBRT)是任意一个不同损失函数的泛化。GBRT是一个灵敏的并且高效程序，可以用在回归和分类中。梯度提升树模型在许多领域中都有使用，如web搜索排行榜和社会生态学中。它主要的思想是，每一次建立模型是在之前建立模型损失函数的梯度下降方向。这句话有一点拗口，损失函数(loss function)描述的是模型的不靠谱程度，损失函数越大，则说明模型越容易出错（其实这里有一个方差、偏差均衡的问题，但是这里就假设损失函数越大，模型越容易出错）。如果我们的模型能够让损失函数持续的下降，则说明我们的模型在不停的改进，而最好的方式就是让损失函数在其梯度（Gradient)的方向上下降。

GRBT的优势：

• 混合数据类型的自然处理
• 预测力强
• 健壮的输出空间

Boosting主要是一种思想，表示“知错就改”。而Gradient Boosting是在这个思想下的一种函数（也可以说是模型）的优化的方法，首先将函数分解为可加的形式（其实所有的函数都是可加的，只是是否好放在这个框架中，以及最终的效果如何）。然后进行m次迭代，通过使得损失函数在梯度方向上减少，最终得到一个优秀的模型。值得一提的是，每次模型在梯度方向上的减少的部分，可以认为是一个“小”的或者“弱”的模型，最终我们会通过加权(也就是每次在梯度方向上下降的距离）的方式将这些“弱”的模型合并起来，形成一个更好的模型。