题目
POJ1904 King’s Quest
分析
题目大意:
有n个王子和n个妹子,王子可能会喜欢多个妹子,现在这些王子要跟自己喜欢的妹子结婚。
给出一个可行的婚配方案(完美匹配),要求所有的可行匹配,使得:每个王子与求得方案中的某一个妹子结婚后,其他喜欢这个妹子的王子仍有其他婚配方案。
(不可行)思路1:
乍一看上去像是二分图匹配。显然,所有妹子与王子都要结婚,没有重婚、没有单身,即“不重不漏“”。那么我们可以通过二分图匹配,不断寻找增广路,每次记录可行匹配,最后枚举给定方案中的每个王子的妹子进行判断。
复杂度应该是 O(n?m2) O ( n ? m 2 ) ,显然TLE。
(不可行)思路2:
我们发现给出的完美匹配还没有用上。思考一下它的用处?不妨在建完二分图后,让给定方案中的妹子向该王子连一条边。观察性质,发现每一些“王子——妹子——王子……”的路径就类似于二分图匹配中的增广路,如果我们按照这写路径不断走下去,相当于模拟了匹配的过程。
可这样只是优化了匈牙利算法递归的时间,仍然TLE。
(可行)思路3:
如果跳出“二分图”这一思维定势,我们不妨尝试其他做法。在思路2的建图过后,我们还可以发现:在每一强连通分量里的王子们,可以通过“强连通分量内部调节”与其他妹子婚配,并且保证联通块内王子和妹子不重不漏。但为什么呢?
首先,根据思路1的“不重不漏”分析,因为一个妹子可以由多个王子连过来,但每个妹子只连向一个王子,一旦形成强联通分量,就意味着大致形成下图所示的情况:(红线表示二分图边,黄线表示后加的边,左边为王子,右边为妹子)
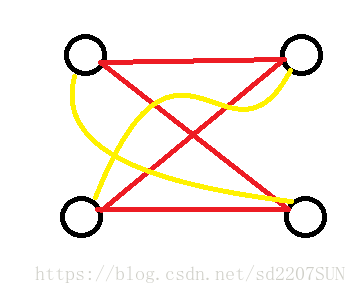
这样,王子可以通过(黄——红——红)找到另一个妹子,妹子可以通过(红——红——黄)找到另一个王子,这样保证了更改后的方案合法。
至于 妹子数=王子数 妹 子 数 = 王 子 数 ,此处反证:若多了几个妹子,那这些妹子也就没有黄色边,也就没法找到另一个可匹配的王子,也就没有刚才描述的路线,不符合题设。多几个王子的情况同理。
思路十分明朗了。建图,缩点,对于每个王子,枚举处在同一强连通分量里的妹子记录答案。
代码
#include<cstdio>
#include<iostream>
using namespace std;
const int maxn=4004,maxm=200002;
struct Edge{int to,next;
}e[maxm+maxn];
int head[maxn],blt[maxn],sta[maxn],dfn[maxn],low[maxn],ans[maxn/2];
bool love[maxn/2][maxn/2];
int n,cnt,top,dfc,rpg;void add(int u,int v)
{e[++cnt].to=v;e[cnt].next=head[u];head[u]=cnt;
}void tarjan(int u)
{dfn[u]=low[u]=++dfc;sta[++top]=u;for(int i=head[u];i;i=e[i].next){int v=e[i].to;if(!dfn[v]){tarjan(v);low[u]=min(low[u],low[v]);}else if(!blt[v])low[u]=min(low[u],dfn[v]);}if(low[u]==dfn[u]){rpg++;while(1){int x=sta[top--];blt[x]=rpg;if(x==u)break;}}
}int main()
{scanf("%d",&n);for(int i=1,t,x;i<=n;i++){scanf("%d",&t);while(t--){scanf("%d",&x);add(i,x+n);love[i][x]=true;}}for(int i=1,x;i<=n;i++){scanf("%d",&x);add(x+n,i);}for(int i=1;i<=(n<<1);i++)if(!dfn[i])tarjan(i);for(int i=1;i<=n;i++){int sum=0;for(int j=1;j<=n;j++)if(blt[i]==blt[j+n]&&love[i][j])ans[++sum]=j;printf("%d ",sum);for(int i=1;i<=sum;i++)printf("%d ",ans[i]);printf("\n");}return 0;
}