一、问题描述
回文子串和回文子序列不同:
子串,一定要连续
子序列,不一定连续
其实最长回文子串是可以转换成LCS来做的,具体方法就是:
将原串生成反向串,然后用dp求原串和反向串的LCS
但是这样缺点也很明显的是O(n*n)的复杂度,即使优化到:滚动数组+下标找反向串,也不能从根本上解决这个算法的低效。
如果想在 O(n) 时间内解决回文子串问题呢?
答案就是Manacher算法,用一句话来概括这个算法:
通过记录已匹配的最右位置和对应的对称中心来跳过一些没用的比较
在下面的代码中,这个已匹配的最右位置就是mx,对称中心就是id。
二、Manacher算法模板
完整模板
int Manacher(string tmp) {memset(P,0,sizeof(P));int len=tmp.size();int k;for(k=0;k<len;k++){s[2*k] = '#';s[2*k+1] = tmp[k];}s[2*k] = '#';s[2*k+1] = '\0';//算法核心len=strlen(s);int mx = 0; //mx 记在i之前的回文串中,延伸至最右端的位置int id=0; //id 记下取得这个最优mx时的 坐标值for (int i=0;i<len;++i) {if( i < mx ) //在当前最优边界左边P[i] = min(P[2*id-i],mx-i);elseP[i]=1;for (;s[i-P[i]] == s[i+P[i]] && s[i-P[i]] != '\0' && s[i+P[i]] != '\0' ; ) //对于超出mx或者P[j]边界的计算P[i]++;if( P[i]+i > mx ) { //当前最佳情况,update mx和idmx = P[i] + i; //最右端情况id = i; //记下坐标}}int res = 0;for (int i=0;i<len;++i) {res = max(res,P[i]);}return res-1;
}三、算法思想
1、预处理
算法在字符串开头、结尾、字符之间都插入特殊字符(这里用’#’),这样就巧妙的把奇数的回文串和偶数的回文串统一起来考虑了(统一为奇数),不然处理回文串会很麻烦。
比如:abc 变成 #a#b#c# 这样有7个字符。
abcd 变成 #a#b#c#d# 有9个字符。
可能有疑问:预处理成这样,后面不是要算回文子串长度的时候,又要减去这些特殊字符吗。
其实不会,因为算法用 P[i] 来记录 i 这个 pos 的最长单臂子串长度,比如 #a#b#c#b#a# 这个单臂子串长度为 #a#b#c,即长度为6,
而这里有一个很好的性质,P[i]-1 就是该回文子串在原串中的长度。即 abcba 就是5
2、核心算法
其实Manacher算法的核心代码很简单,但是理解起来感觉相当精妙,果然是算法是代码写成的诗歌。
核心代码:
//算法核心
len=strlen(s);
int mx = 0; //mx 记在i之前的回文串中,延伸至最右端的位置
int id=0; //id 记下取得这个最优mx时的 坐标值
for (int i=0;i<len;++i) {if( i < mx ) //在当前最优边界左边P[i] = min(P[2*id-i],mx-i); //算出对称初始值elseP[i]=1; //如果超出mx边界,P[i]初始值为1for (;s[i-P[i]] == s[i+P[i]] && s[i-P[i]] != '\0' && s[i+P[i]] != '\0' ; ) //对于超出mx或者P[j]边界的计算P[i]++;if( P[i]+i > mx ) { //当前最佳情况,update mx和idmx = P[i] + i; //最右端情况id = i; //记下坐标}
}算法开始是会通过一个if else判断来决定P[i]的初始值。
算法的关键点就在这里:
if( i < mx ) //在当前最优边界左边P[i]= min(P[2*id-i],mx-i); //算出对称初始值
elseP[i]=1; //如果超出mx边界,P[i]初始值为1那为什么是 min(P[2*id-i],mx-i) 呢?
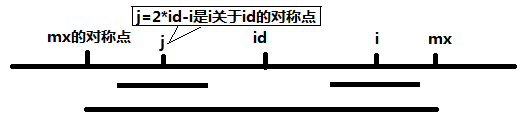
3.2.1 取 P[2*id-i],即 P[2*id-i] <= mx-i
这种情况下,整个 中心i(或中心j) 的子串都涵盖在 中心为 id,长度为 mx-id 的巨型臂膀下,由于 id为中心的完全对称,必然 P[j] == P[i],
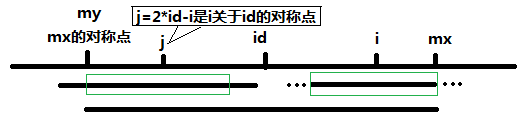
3.2.2 取 mx-i,即 P[2*id-i] >= mx-i
这种情况下,是 id 的臂展无法完全包裹 以i为中心的臂展时:
根据对称性可知,图中两个绿框所包围的部分是相同的,也就是说以 i 为中心的回文子串,其向右至少会扩张到mx的位置,也就是说 P[i] >= mx - i。至于mx之后的部分是否对称,就只能一个一个匹配了。
另外特别要注意的是,要注意设置“哨兵”,也就是自己设置特殊字符或者’\0’代表边界,不然后面的
for (;s[i-P[i]] == s[i+P[i]] ; P[i]++);就会越界。
给出我画出的原手稿
下图中,当i为13时,臂展最大,但是这个字符的P[i]初始化为6,即 i = 5那个点 ‘c’。
参考资料
[1] http://www.cnblogs.com/biyeymyhjob/archive/2012/10/04/2711527.html
[2] http://blog.csdn.net/ggggiqnypgjg/article/details/6645824/