提纲:
分类模型 与 Loss 函数的定义,
为什么不能用 Classification Error,
- Cross Entropy 的效果对比,
为什么不用 Mean Squared Error,
- 定量理解 Cross Entropy,
- 总结,
- 参考资料。
分类模型 与 Loss 函数的定义
分类和回归问题,是监督学习的 2 大分支。
不同点在于:分类问题的目标变量是离散的,而回归是连续的数值。
本文讨论的是分类模型。
分类模型的例子:
根据年龄、性别、年收入等相互独立的特征,
预测一个人的政治倾向(民主党、共和党、其他党派)。
为了训练模型,必须先定义衡量模型好与坏的标准。
在机器学习中,我们使用 loss / cost,即,
当前模型与理想模型的差距。
训练的目的,就是不断缩小 loss / cost.
为什么不能用 classification error
大多数人望文生义的 loss,可能是上面这个公式。
我们用一个的实际模型来看 classification error 的弊端。
使用 3 组训练数据,
computed 一栏是预测结果,targets 是预期结果。
二者的数字,都可以理解为概率。
correct 一栏表示预测是否正确。
模型 1
computed | targets | correct?
------------------------------------------------
0.3 0.3 0.4 | 0 0 1 (democrat) | yes
0.3 0.4 0.3 | 0 1 0 (republican) | yes
0.1 0.2 0.7 | 1 0 0 (other) | no
item 1 和 2 以非常微弱的优势判断正确,item 3 则彻底错误。
模型 2
computed | targets | correct?
-------------------------------------------------
0.1 0.2 0.7 | 0 0 1 (democrat) | yes
0.1 0.7 0.2 | 0 1 0 (republican) | yes
0.3 0.4 0.3 | 1 0 0 (other) | no
item 1 和 2 的判断非常精准,item 3 判错,但比较轻。
结论
2 个模型的 classification error 相等,但模型 2 要明显优于模型 1.
classification error 很难精确描述模型与理想模型之间的距离。
Cross-Entropy 的效果对比
TensoFlow 官网的 MNIST For ML Beginners 中 cross entropy 的计算公式是:
根据公式,
第一个模型中第一项的 cross-entropy 是:
-( (ln(0.3)*0) + (ln(0.3)*0) + (ln(0.4)*1) ) = -ln(0.4)
所以,第一个模型的 ACE ( average cross-entropy error ) 是
-(ln(0.4) + ln(0.4) + ln(0.1)) / 3 = 1.38
第二个模型的 ACE 是:
(ln(0.7) + ln(0.7) + ln(0.3)) / 3 = 0.64
结论
ACE 结果准确的体现了模型 2 优于模型 1。
cross-entropy 更清晰的描述了模型与理想模型的距离。
为什么不用 Mean Squared Error (平方和)
若使用 MSE(mean squared error),
第一个模型第一项的 loss 是
(0.3 - 0)^2 + (0.3 - 0)^2 + (0.4 - 1)^2 = 0.09 + 0.09 + 0.36 = 0.54
第一个模型的 loss 是
(0.54 + 0.54 + 1.34) / 3 = 0.81
第二个模型的 loss 是
(0.14 + 0.14 + 0.74) / 3 = 0.34
看起来也是蛮不错的。为何不用?
分类问题,最后必须是 one hot 形式算出各 label 的概率,
然后通过 argmax 选出最终的分类。
(稍后用一篇文章解释必须 one hot 的原因)
在计算各个 label 概率的时候,用的是 softmax 函数。
如果用 MSE 计算 loss,
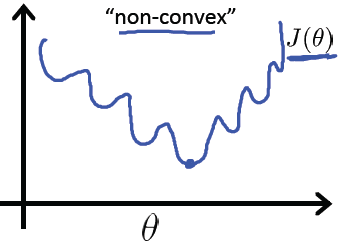
输出的曲线是波动的,有很多局部的极值点。
即,非凸优化问题 (non-convex)
cross entropy 计算 loss,则依旧是一个凸优化问题,
用梯度下降求解时,凸优化问题有很好的收敛特性。
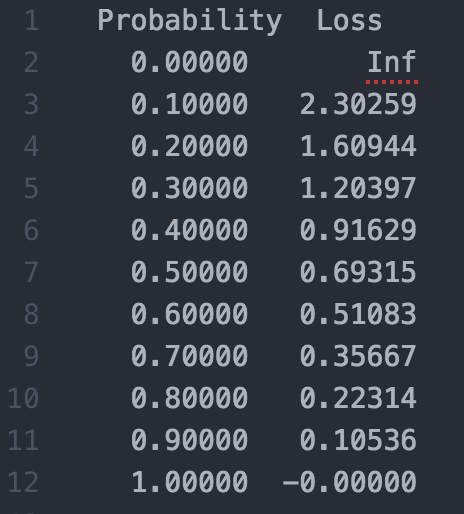
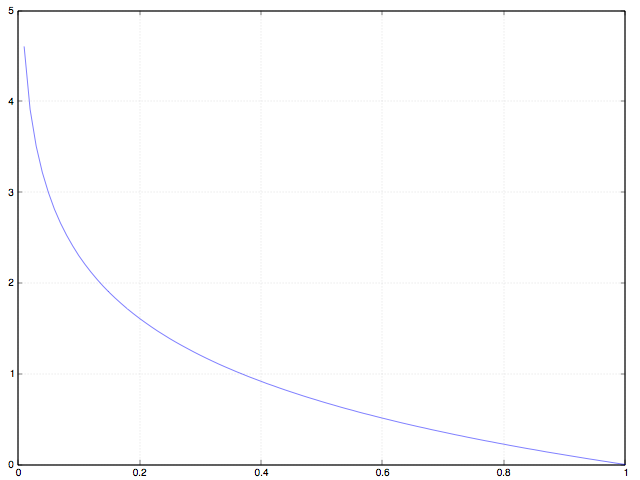
定量理解 cross entropy
训练的时候,loss 为 0.1 是什么概念,0.01 呢?总结
分类问题,都用 onehot + cross entropy
training 过程中,分类问题用 cross entropy,回归问题用 mean squared error。
training 之后,validation / testing 时,使用 classification error,更直观,而且是我们最关注的指标。
参考资料
分类模型的本质是组合数学问题 A Tutorial on the Cross-Entropy Method
文中的对比模型来自:Why You Should Use Cross-Entropy Error Instead Of Classification Error Or Mean Squared Error For Neural Network Classifier Training
关于 cross entropy 与 MSE 的详细对比:http://books.jackon.me/Cross-Entropy-vs-Squared-Error-Training-a-Theoretical-and-Experimental-Comparison.pdf
Ng 的公开课中有详细讨论 logistic regression 的 loss 函数 https://www.coursera.org/learn/machine-learning/lecture/1XG8G/cost-function