线性插值
先讲一下线性插值:已知数据 (x0, y0) 与 (x1, y1),要计算 [x0, x1] 区间内某一位置 x 在直线上的y值(反过来也是一样,略):

上面比较好理解吧,仔细看就是用x和x0,x1的距离作为一个权重,用于y0和y1的加权。双线性插值本质上就是在两个方向上做线性插值。
线性插值的几何意义如右图所示,即为利用过点 和 的直线 来近似原函数 。线性插值相比其他插值方式,如抛物线插值,具有简单、方便的特点。线性插值的几何意义即为概述图中利用过A点和B点的直线来近似表示原函数。线性插值可以用来近似代替原函数,也可以用来计算得到查表过程中表中没有的数值。
双线性插值
在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值:
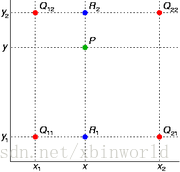
假如我们想得到未知函数 f 在点 P = (x, y) 的值,假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。
首先在
x方向进行线性插值,得到R1和R2,然后在
y方向进行线性插值,得到P.
这样就得到所要的结果
f(
x,
y).
其中红色点Q11,Q12,Q21,Q22为已知的4个像素点.
线性插值的结果与插值的顺序无关。首先进行
y
方向的插值,然后进行
x
方向的插值,所得到的结果是一样的。双线性插值的结果与先进行哪个方向的插值无关。