本篇博客转载自:
VAE(Variational Autoencoder)的原理
OpenAI实习生讲解变分自编码机
以上两篇文章翻译自Kevin Frans的英文博客.
英文原文:Variational Autoencoders Explained
论文链接:Auto-encoding variational bayes
论文的理论推导:变分自编码器(VAEs)
以下为正文:
我曾经讲解过一次生成式对抗网络(GAN),谈的是用它来生成逼真图像的一个简单例子。
但这中间有些问题,即单纯使用GAN存在两大不利因素。
首先,这里的图像生成自某些随机的噪点。如果你想生成的是一张特定细节的图像,除了遍历初始噪点的整个分布范围,你没有别的办法来找出它们的值。
其次,生成式对抗模型只能区分出图像的“真”、“假”。你没有办法强制它所生成猫图必须看起来像猫。这就造成了一个问题,就是它所生成的图像不是参照真实的物体,而是参照的他们在图片中的样子,风格上不会特别写实。
如何解决这两个问题呢?
我会在本文中介绍另一种神经网络——变分自编码机,来解决这两个问题。
什么是变分自编码机?
为了理解VAE,我们首先从最简单的网络说起,然后再一步一步添加额外的部分。
一个描述神经网络的常见方法是近似一些我们想建模的函数。然而神经网络也可以被看做是携带信息的数据结构。
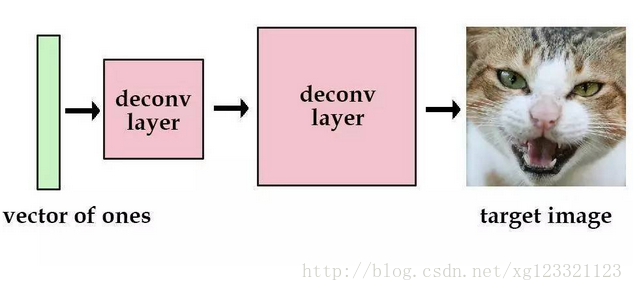
假如我们有一个带有解卷积层的网络,我们设置输入为值全为1的向量,输出为一张图像。然后,我们可以训练这个网络去减小重构图像和原始图像的平均平方误差。那么训练完后,这个图像的信息就被保留在了网络的参数中。
现在,我们尝试使用更多的图片。这次我们用one-hot向量而不是全1向量。我们用[1, 0, 0, 0]代表猫,用[0, 1, 0, 0]代表狗。虽然这没什么问题,但是我们最多只能储存4张图片。当然,我们也可以增加向量的长度和网络的参数,那么我们可以获得更多的图片。
但是,这样的向量很稀疏。为了解决这个问题,我们想使用实数值向量而不是0,1向量。我们可认为这种实数值向量是原图片的一种编码,这也就引出了编码/解码的概念。举个例子,[3.3, 4.5, 2.1, 9.8]代表猫,[3.4, 2.1, 6.7, 4.2] 代表狗。这个已知的初始向量可以作为我们的潜在变量。
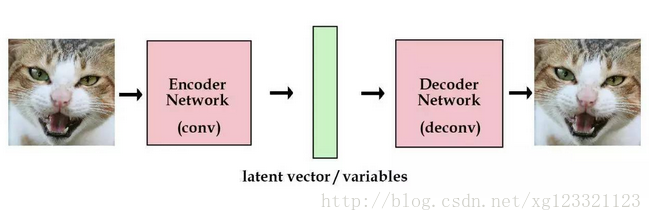
如果像我上面一样,随机初始化一些向量去代表图片的编码,这不是一个很好的办法,我们更希望计算机能帮我们自动编码。在autoencoder模型中,我们加入一个编码器,它能帮我们把图片编码成向量。然后解码器能够把这些向量恢复成图片。
我们现在获得了一个有点实际用处的网络了。而且我们现在能训练任意多的图片了。如果我们把这些图片的编码向量存在来,那以后我们就能通过这些编码向量来重构我们的图像。我们称之为标准自编码器。
但是,我们想建一个产生式模型,而不是一个只是储存图片的网络。现在我们还不能产生任何未知的东西,因为我们不能随意产生合理的潜在变量。因为合理的潜在变量都是编码器从原始图片中产生的。
这里有个简单的解决办法。我们可以对编码器添加约束,就是强迫它产生服从单位高斯分布的潜在变量。正式这种约束,把VAE和标准自编码器给区分开来了。
现在,产生新的图片也变得容易:我们只要从单位高斯分布中进行采样,然后把它传给解码器就可以了。
事实上,我们还需要在重构图片的精确度和单位高斯分布的拟合度上进行权衡。
我们可以让网络自己去决定这种权衡。对于我们的损失函数,我们可以把这两方面进行加和。一方面,是图片的重构误差,我们可以用平均平方误差来度量,另一方面。我们可以用KL散度(KL散度介绍)来度量我们潜在变量的分布和单位高斯分布的差异。
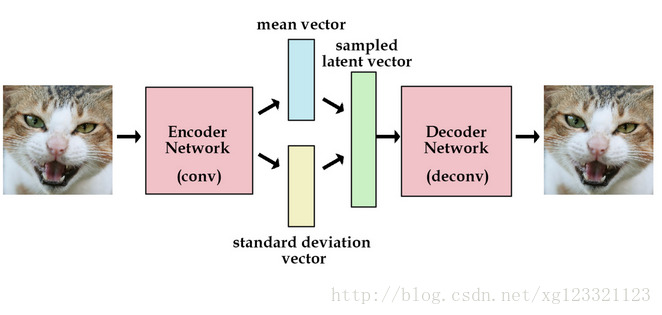
为了优化KL散度,我们需要应用一个简单的参数重构技巧:不像标准自编码器那样产生实数值向量,VAE的编码器会产生两个向量:一个是均值向量,一个是标准差向量。
我们可以这样来计算KL散度:
z_mean and z_stddev are two vectors generated by encoder networklatent_loss = 0.5 * tf.reduce_sum(tf.square(z_mean) + tf.square(z_stddev) - tf.log(tf.square(z_stddev)) - 1,1)
- 1
- 2
- 3
当我们计算解码器的loss时,我们就可以从标准差向量中采样,然后加到我们的均值向量上,就得到了编码去需要的潜在变量。
VAE除了能让我们能够自己产生随机的潜在变量,这种约束也能提高网络的产生图片的能力。
为了更加形象,我们可以认为潜在变量是一种数据的转换。
我们假设我们有一堆实数在区间[0, 10]上,每个实数对应一个物体名字。比如,5.43对应着苹果,5.44对应着香蕉。当有个人给你个5.43,你就知道这是代表着苹果。我们能用这种方法够编码无穷多的物体,因为[0, 10]之间的实数有无穷多个。
但是,如果某人给你一个实数的时候其实是加了高斯噪声的呢?比如你接受到了5.43,原始的数值可能是 [4.4 ~ 6.4]之间的任意一个数,真实值可能是5.44(香蕉)。
如果给的方差越大,那么这个平均值向量所携带的可用信息就越少。
现在,我们可以把这种逻辑用在编码器和解码器上。编码越有效,那么标准差向量就越能趋近于标准高斯分布的单位标准差。
这种约束迫使编码器更加高效,并能够产生信息丰富的潜在变量。这也提高了产生图片的性能。而且我们的潜变量不仅可以随机产生,也能从未经过训练的图片输入编码器后产生。
VAE的效果如何?
我做了一些小实验来测试VAE在MNIST手写数字数据集上的表现:
使用VAE的优点是我们可以通过编码解码的步骤,直接比较重建图片和原始图片的差异,但是GAN做不到。
另外,VAE的一个缺点是没有使用对抗网络,所以会更趋向于产生模糊的图片。
也有一些需要结合VAE和GAN的研究工作:采用相同的 编码器-解码器 配置,但使用对抗网络来训练解码器。
更多细节可以参考以下的论文和博客:
Autoencoding beyond pixels using a learned similarity metric
Generating Large Images from Latent Vectors
你也可以从这里获得这篇博客的代码,这是原始的代码。