Unsupervised Deep Embedding for Clustering Analysis
1.Introduction
聚类在无监督机器学习中由这几个方面进行了研究:如何定义一个类?什么是正确的距离矩阵?如何对数据进行有效聚类?如何验证聚类结果?至今已有许多工作致力于距离函数与嵌入方法的研究,用于执行聚类的特征空间无监督学习的的研究工作还比较少。对于所有最简单的图像数据集,使用欧氏距离的聚类完全失效。本文希望找到一种方案,可以联合解决特征空间学习与聚类关系判别。
本文定义了一个由数据空间X到低维特征空间Z的参数化非线性映射,在低维空间优化聚类目标。此前的工作在数据空间或是浅层线性嵌入空间上进行操作,本文在聚类目标上采用反向传播的SGD来学习映射,该映射被深度神经网络进行了参数化,被称为DEC。
如何优化DEC?本文希望同时解决聚类分配与潜在特征表示的学习,然而无法通过标签数据训练DNN。因此本文提出使用目前的soft cluster assignment派生出的辅助目标分布来迭代细化聚类。这个过程可以同时改进聚类与特征表示。
2.Related work
有些方法可以拥有解决一系列问题,但是它们的距离矩阵限于初始数据空间,当输入维度过高时,它们会变得没有效果。
还有一些方法为了解决高维输入空间的问题:首先使用k-means聚类数据,然后将数据投影到低维使之类间差异最大化。这种框架受限于线性嵌入。
最小化数据分布与嵌入分布间的Kullback-Leibler (KL) divergence被用于数据可视化与降维,例如t-SNE,是一个非参数的方法,其参数化变种通过DNN来参数化embedding。
我们定义了基于质心的概率分布,并最小化其与辅助目标分布的KL偏差,以同时改进聚类分配和特征表示,而不是最小化KL散度以产生忠实于原始数据空间中的距离的嵌入。
3.Deep embedded clustering
考虑 n n n个点的聚类问题,将划分为 k k k个类, j = 1 , 2 … … k j=1,2……k j=1,2……k表示 k k k个聚类中心。并非直接在聚类空间X中聚类,我们首先将数据使用非线性映射: X → Z X→Z X→Z, θ \theta θ是学习到的参数, Z Z Z是潜在特征空间。 Z Z Z的维度一般来说要比 X X X小的多。使用DNN来参数化。
DEC算法同时学习特征空间 Z Z Z的 k k k个聚类中心和用于映射的参数θ。DEC有两个阶段:(1)使用deep autoencoder初始化参数 (2)参数优化(聚类),该过程中,本文在计算辅助目标分布于最小化KL之间交替进行。本文从参数优化过程开始阐述,给定 θ \theta θ与参数中心 μ \mu μ的初始估计。
3.1 通过 KL divergence 聚类
给定 θ \theta θ与参数中心 u u u的初始估计,本文提出使用分两步迭代进行的非监督算法来改进聚类。第一步:计算嵌入点与聚类中心间的soft assignment(当某点与某聚类中心依概率符合分布时,将其分配给该中心);第二步:更新映射,通过从"使用辅助目标分布的高自信assignments"中学习来细化聚类中心。这个过程直到某种收敛准则符合而停止。
3.1.1 SOFT ASSIGNMENT
本文使用学生 t t t-分布作为kernel来衡量嵌入点 z i z_i zi?与中心点 μ j \mu_j μj?的相似性:
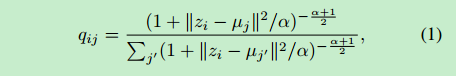
其中, 对应于的嵌入点, α \alpha α是 t t t分布的自由度,可以解释为将样本 i i i分配给聚类 j j j的概率(soft assignment)。因为在非监督学习中无法交叉验证 α \alpha α,所以没必要学习它,统一设置为1。
PS:软分配概念
3.1.2 KL DIVERGENCE MINIMIZATION
在辅助目标函数的帮助下,本文从高自信assignments中学习,迭代精炼聚类。本文模型通过将soft assignment与目标分布进行匹配来进行训练。为实现该目的,本文将目标函数设置为soft assignments与辅助分布之间的KL divergence损失:
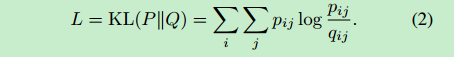
目标分布P的选择对于DEC的表现来说至关重要。一般做法是将每个 p i p_i pi?设置为高于置信度阈值的数据点的delta分布(到最近的质心),并忽略其余部分。然而,由于 q i q_i qi?是soft assignments,因此随 q i q_i qi?使用softer probabilistic targets是一件自然而然的选择。本文希望target distribution具有以下性质:(1)强化预测,(2)更加重视高可信度地分配的数据点,(3)规范每个质心的损失贡献,以防止大类扭曲隐藏的特征空间。
本文实验通过首先将 q i q_i qi?提高到第次幂然后按每个簇的频率归一化来计算 p i p_i pi?:
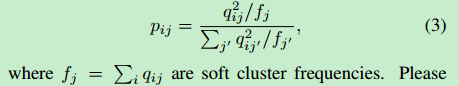
其中, f j = ∑ i q i j f_j=\sum_i q_{ij} fj?=∑i?qij?是软聚类频率。
3.1.3 OPTIMIZATION
本文联合优化聚类中心 u j u_j uj?和DNN的参数 θ \theta θ(通过动量SGD)。L的梯度与数据点 z i z_i zi?的嵌入特征空间和每个聚类中心 u j u_j uj?有关,如下计算:
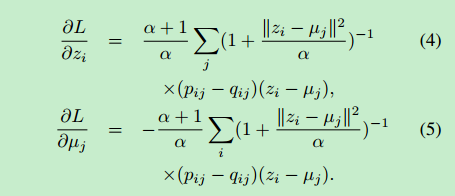
梯度 ? L ? z i \frac{\partial L}{\partial z_i} ?zi??L?随后被传递给DNN,用于标准反向传播来计算DNN的参数梯度 ? L ? θ \frac{\partial L}{\partial \theta} ?θ?L?为了发现聚类分配的目的,本文设置当少于总量的tol%数据点在连续迭代间改变其所属类时停止优化。
3.2 参数初始化

使用堆叠自动编码器(SAE)初始化DEC的参数 θ \theta θ;
使用k-means对用SAE得到的嵌入表示聚类,得到聚类中心作为DEC模型的初始化质心。
总体来说,第一步是最小化重建误差(初始化),第二步(DEC模型)是最小化KL散度。论文定义了基于质心的概率分布,并最小化其与辅助目标分布的KL偏差,以同时改进聚类分配和特征表示,而不是最小化KL散度以产生忠实于原始数据空间中的距离的嵌入。
4.实验
数据集
MNIST:手写数字,28*28的灰度图
STL-10:彩色图,96*96,将HOG特征和8×8彩色图连接起来,用作输入。
路透社:路透社包含大约810000个标有类别树的英文新闻报道 的一部分
评价指标
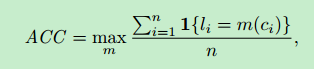
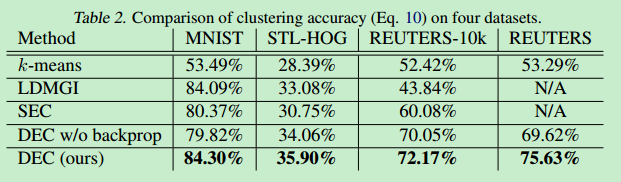
实验结果
参考
Unsupervised Deep Embedding for Clustering Analysis
https://blog.csdn.net/Weyoung_/article/details/79407651
