k-Shape: Efficient and Accurate Clustering of Time Series
John Paparrizos Luis Gravano Columbia University
ACM SIGMOD 2015
主要贡献
- 提出一种新的对尺度和漂移具有不变性的距离度量
- 提出一种新的计算聚类中心的方法
- 提出一种通用性强的时间序列聚类算法——k-shape算法
- 通过实验验证算法为state-of-the-art
目前聚类算法存在的问题
- 无法处理大的数据集,计算复杂度高
- 通用性不好,一般只针对特定问题有效
时间序列比较的关键问题——处理各种distortions(扭曲?)
- Scaling and transform invariances 量纲不同、映射不变性
- Shift invariances 序列相似但是存在相位漂移
- Uniform scaling invariance 序列的长度不一致(压缩、拉伸)
- Occlusion invariance 序列存在缺失
本文主要解决前两个问题,第一个问题通过z-normalization可以解决。
基于互相关的度量SBD——解决相位漂移问题
固定序列y,移动序列x,找到最佳匹配
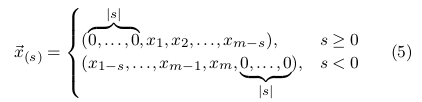
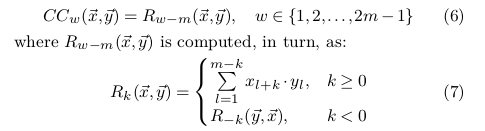
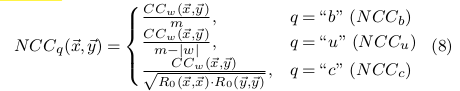
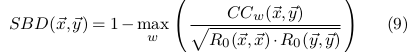

卷积定理:两个信号的卷积可计算为两个信号的DFT(离散傅里叶变换)的乘积的IDFT(逆离散傅里叶变换)。
由于直接计算DFT和IDFT,时间复杂度为O(m2),这里采用FFT,使复杂度降为O(mlogm)。
聚类中心的计算

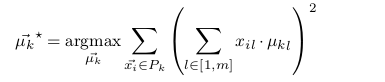
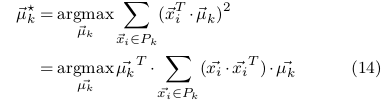

这样就变成了求瑞利商的问题,于是最大值为矩阵M对应最大特征值的特征向量。
k-shape算法

- 根据给定聚类中心,更新类内成员,将序列归到距离最近的聚类中心所在的簇
- 重新计算聚类中心
实验结果

这里的“>”, “=”, and “<”代表与k-AVG+ED比,算法的表现更好、持平、更差的数据集的数量。“Better”和“Worse”指的是好于k-AVG+SBD算法。
如何衡量算法的好坏?
- 时间复杂度
- 与其他算法的比较
- 准确率、精确率、召回率、ROC、MSE等等
- Wilcoxon Signed Ranks Test 比较两种算法
- 使用Friedman test配合Nemenyi test做post-hoc 比较多种算法