题目背景:
分析:这个题,我真的很想呵呵,当时听满分神犇讲了一次,然后学长讲了一次,然后默默的自己看了n次,然后在给别人讲了两次,才终于算是基本懂了······现在让我写,恐怕还是只有呵呵······我们先一步步进行考虑,首先对于一条链上的某一个点,他在这一条链上的统计次数,是这条链上比它的权值小的点的个数加1次,对于那一个1,我们完全可以通过dfs判断一个点会出现在多少的链中,然后比它小的点,我们可以通过直接以每一个点为根,分别dfs一次,然后求得每一个点到当前根路径上,比根的权值小的点的个数,因为我们可以发现,这个性质是具有可并性的,比如,点x在链A上有a个权值比它小的点,在链B上有b个权值比它小的点,那么在AB长链上,点x就会被统计a + b + 1次(前提是链A与链B不重合),那么我们就可以选择支持这一个换根操作来统计每个点的贡献,这样做的复杂度是O(n2)的,我们可以过60分的数据。
Source:
#include #include #include #include #include #include #include #include using namespace std; inline char read() { static const int IN_LEN = 1024 * 1024; static char buf[IN_LEN], *s, *t; if (s == t) { t = (s = buf) + fread(buf, 1, IN_LEN, stdin); if (s == t) return -1; } return *s++; } template inline bool R(T &x) { static char c; static bool iosig; for (c = read(), iosig = false; !isdigit(c); c = read()) { if (c == -1) return false; if (c == '-') iosig = true; } for (x = 0; isdigit(c); c = read()) x = (x << 3) + (x << 1) + (c ^ '0'); if (iosig) x = -x; return true; } const int OUT_LEN = 1024 * 1024; char obuf[OUT_LEN], *oh = obuf; inline void writechar(char c) { if (oh == obuf + OUT_LEN) fwrite(obuf, 1, OUT_LEN, stdout), oh = obuf; *oh++ = c; } template inline void W(T x) { static int buf[30], cnt; if (!x) writechar(48); else { if (x < 0) writechar('-'), x = -x; for (cnt = 0; x; x /= 10) buf[++cnt] = x % 10 + 48; while (cnt) writechar(buf[cnt--]); } } inline void flush() { fwrite(obuf, 1, oh - obuf, stdout); } const int MAXN = 100000 + 10; const int mod = 1e9 + 7; int n, x, y; int v[MAXN], size[MAXN]; vector edge[MAXN]; inline void create(int x, int y) { edge[x].push_back(y); edge[y].push_back(x); } inline void readin() { R(n); for (int i = 1; i < n; ++i) R(x), R(y), create(x, y); for (int i = 1; i <= n; ++i) R(v[i]); } int id, val, cnt; inline void add(int &x, int t) { x += t; if (x >= mod) x -= mod; } inline void dfs(int cur, int fa, int w) { if (v[cur] < val || v[cur] == val && cur < id) w++; add(cnt, w), size[cur] = 1; for (int p = 0; p < edge[cur].size(); ++p) if (edge[cur][p] != fa) { dfs(edge[cur][p], cur, w); size[cur] += size[edge[cur][p]]; } } inline void work() { int cur, del, ans = 0; for (int i = 1; i <= n; ++i) { id = i, val = v[i], cur = 1, del = 0; for (int p = 0; p < edge[i].size(); ++p) { cnt = 0, dfs(edge[i][p], i, 0); add(ans, 1LL * cnt * (n - size[edge[i][p]]) * v[i] % mod); add(del, 1LL * cur * size[edge[i][p]] % mod); add(cur, size[edge[i][p]]); } add(ans, 1LL * del * v[i] % mod); } W(ans); } int main() { // freopen("in.in", "r", stdin); readin(); work(); flush(); return 0; } 现在我们再来考虑如何做到100分,我们看上面的60分的代码,我们可以发现,针对一个特定的根,对于一个权值比它小的点,针对这一个特定根的贡献应该是当前这个点的子树的大小size,(如下面代码片段)
inline void dfs(int cur, int fa, int w) {
if (v[cur] < val || v[cur] == val && cur < id) w++;
add(cnt, w), size[cur] = 1;
/* 走过的时候直接走过的时候直接全部加入
每一次在子树中就会被加入*/
for (int p = 0; p < edge[cur].size(); ++p)
if (edge[cur][p] != fa) {
dfs(edge[cur][p], cur, w);
size[cur] += size[edge[cur][p]];
}
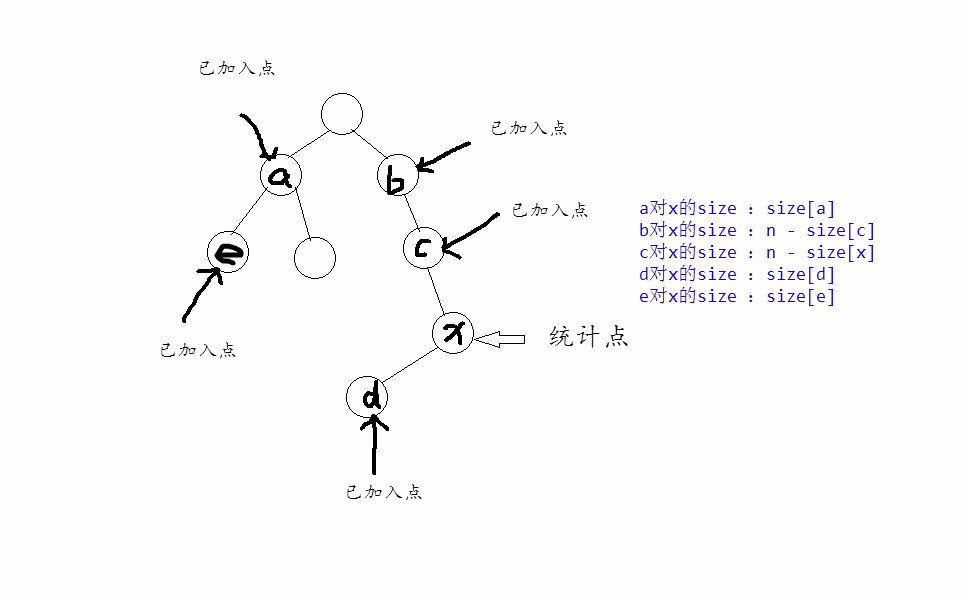
}在我们访问它的每一个子树节点时,我们都可以发现我们都会将吗,目前统计的全部贡献加入总答案,也就是说,这个点对当前根的贡献是它的子树大小,然后,我们就可以发现,对于某一个特定的点,比他权值大的点,对统计当前点的答案是没有影响的,那么我们就可以选择对于每一个点进行权值的排序,然后一次从小到大加入,这样,然后我们在dfs序上搞一个bit,每一次将新加入的节点的size在上面加入即可,这个时候,我们就又会发现一个问题,如果我们统计的点不是树根,这个点到根路径上的权值比它小的点的size的计算是不能遵循最开始的dfs时获得的值的,而是应该为整棵树的大小减去其在当前的统计点到根路径上的儿子的大小,(直接说可能会比较抽象,见下面的图片),
之后,我们又来考虑如何统计,首先,我们可以比较容易的统计出除掉当前的统计点到根路径上的其他点对统计点的贡献,然后考虑如何统计这一条路径,首先对于每一个点都会有一个total size即n,我们可以在重新开一个bit,在每一次加入新的点的时候,在他的子树上全部加一,然后统计的时候可以直接计算有多少个1,而得到n的个数,之后对于当前的加入点的儿子该如何除掉,我们完全可以再开一个dfs序上的bit,在他的每一个儿子的子树上打上当前儿子的size即可,然后对于每一个点的统计只需要用bit1中的数 – bit2中的数 n – bit3中的数就可以了。(详情见代码)
#include #include #include #include #include #include #include #include using namespace std; inline char read() { static const int IN_LEN = 1024 * 1024; static char buf[IN_LEN], *s, *t; if (s == t) { t = (s = buf) + fread(buf, 1, IN_LEN, stdin); if (s == t) return -1; } return *s++; } template inline bool R(T &x) { static char c; static bool iosig; for (c = read(), iosig = false; !isdigit(c); c = read()) { if (c == -1) return false; if (c == '-') iosig = true; } for (x = 0; isdigit(c); c = read()) x = (x << 3) + (x << 1) + (c ^ '0'); if (iosig) x = -x; return true; } const int OUT_LEN = 1024 * 1024; char obuf[OUT_LEN], *oh = obuf; inline void writechar(char c) { if (oh == obuf + OUT_LEN) fwrite(obuf, 1, OUT_LEN, stdout), oh = obuf; *oh++ = c; } template inline void W(T x) { static int buf[30], cnt; if (!x) writechar(48); else { if (x < 0) writechar('-'), x = -x; for (cnt = 0; x; x /= 10) buf[++cnt] = x % 10 + 48; while (cnt) writechar(buf[cnt--]); } } inline void flush() { fwrite(obuf, 1, oh - obuf, stdout); } const int MAXN = 100000 + 10; const int mod = 1e9 + 7; vector edge[MAXN]; int n, x, y, cnt, sum; int v[MAXN], bit1[MAXN], bit2[MAXN], bit3[MAXN]; int in[MAXN], out[MAXN], father[MAXN], size[MAXN]; struct data { int id, val; bool operator < (const data &a) const { return (val == a.val) ? (id < a.id) : (val < a.val); } } node[MAXN]; template inline void add(T &x, int t) { x += t; if (x >= mod) x -= mod; if (x < 0) x += mod; } inline int lowbit(int i) { return (i & (-i)); } inline void modify(int i, int val, int *bit) { /*树状数组实现单点修改*/ for (; i <= n; i += lowbit(i)) add(bit[i], val); add(sum, val); } inline void modify(int l, int r, int val, int *bit) { /*树状数组实现区间修改*/ for (int i = l - 1; i; i -= lowbit(i)) add(bit[i], -val); for (int i = r; i; i -= lowbit(i)) add(bit[i], val); } inline int query(int i, int *bit) { /*单点查询*/ int ans = 0; for (ans = 0; i <= n; i += lowbit(i)) add(ans, bit[i]); return add(ans, 0), ans; } inline int query(int l, int r, int *bit) { /*区间查询*/ int ans = 0; for (int i = l - 1; i; i -= lowbit(i)) add(ans, -bit[i]); for (int i = r; i; i -= lowbit(i)) add(ans, bit[i]); return add(ans, 0), ans; } inline void create(int x, int y) { edge[x].push_back(y); edge[y].push_back(x); } inline void readin() { R(n); for (int i = 1; i < n; ++i) R(x), R(y), create(x, y); for (int i = 1; i <= n; ++i) R(node[i].val), v[i] = node[i].val, node[i].id = i; } inline void dfs(int cur, int fa) { /*dfs求得dfs序*/ father[cur] = fa, in[cur] = ++cnt, size[cur] = 1; for (int p = 0; p < edge[cur].size(); ++p) if (edge[cur][p] != fa) dfs(edge[cur][p], cur), size[cur] += size[edge[cur][p]]; out[cur] = cnt; } int ans = 0; inline void solve(int cur) { long long del = 1, ret = 0; for (int p = 0; p < edge[cur].size(); ++p) { if (edge[cur][p] == father[cur]) { /*出题上面的子树*/ long long sum1 = (sum - query(in[cur], out[cur], bit1)) % mod; long long sum2 = query(in[cur], bit2); long long sum3 = query(in[cur], bit3); /*sum1除了自身子树以外的其他点的size*/ /*sum2当前点到根路径上的权值更小的点的个数*/ long long temp = (sum1 - sum3 + (1LL * sum2 * n) % mod) % mod; /*计算贡献*/ add(ret, 1LL * temp * size[cur] % mod); /*将贡献加入答案*/ add(ret, 1LL * (n - size[cur]) * del % mod); /*统计当前统计点经过的链长*/ del += n - size[cur]; } else { int sum1 = query(in[edge[cur][p]], out[edge[cur][p]], bit1); /*分开统计每一个子树的贡献*/ add(ret, 1LL * sum1 * (n - size[edge[cur][p]]) % mod); add(ret, 1LL * size[edge[cur][p]] * del % mod); del += size[edge[cur][p]]; } } add(ans, 1LL * ret * v[cur] % mod); } inline void work() { dfs(1, 1); sort(node + 1, node + n + 1); /*将结点按权值进行排序*/ for (int i = 1, p; i <= n; ++i) { solve(p = node[i].id); modify(in[p], size[p], bit1); /*在第一个bit中计入当前点的size*/ modify(in[p], out[p], 1, bit2); /*在第二个bit中,在当前点的子树上区间加1*/ modify(in[p], out[p], size[p], bit3); /*在第三个bit中,在当前点的子树上打上自己的size explain:因为我们如果发现这个点在统计点到根的路径上,那么我们需要 首先出去之前在bit1中存储的size[p],因为本来我们需要减去bit3中的 儿子的size,那么可以把其自己的size也一并存入来做减*/ for (int j = 0; j < edge[p].size(); ++j) if (edge[p][j] != father[p]) /*在bit3中的对应的子树上放入当前儿子的size*/ modify(in[edge[p][j]], out[edge[p][j]], size[edge[p][j]], bit3); } W((ans % mod + mod) % mod); } int main() { // freopen("in.in", "r", stdin); readin(); work(); flush(); return 0; }