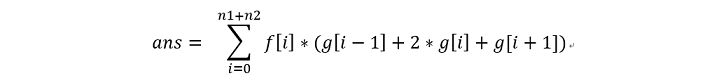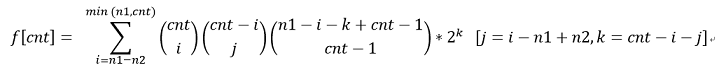计数
题目背景:
BJ模拟2017 D1T1
分析:DP
考虑最后的结果,一定是一些由A,B组成的合法段,和一些由C,D组成的合法段交错连接,我们定义f[i]表示,把A,B分成i个合法段的方案数,g[i]表示,把C,D分成i个合法段的方案数,那么显然答案就是:
显然,可以选择,将i - 1段插在i段之间的空隙,或者将i段插在i段之间的空隙和前面,或者i段之间的空隙和后面,或者将i + 1段插在i段之间和前后。显然f[i]和g[i]的求得方式是类似的,我们只讨论其中之一就可以了。对于两个字母的合法段只有四种情况,(1)ABAB…A,(2)BABA…B,(3)ABAB…AB,(4)BABA…BA,因为后两种情况中的A,B个数相同,那么显然(1) - (2) = n1 - n2,因为A,B个数之差固定,所以,我们只需要枚举其中一个的个数,就可以获得另外一个了,对于f[cnt],第(1)种情况出现了i次,第(2)种出现了j = i - n1 + n2次,那么(3), (4)种,共同出现了k = cnt - i - j次,显然(3), (4)是可以等价考虑的,我们直接全部当成(3)情况,然后最后乘上2k就可以了,有了i, j, k我们相当于在i个位置,先放置了一个A,在j个位置先放置了一个B,k个位置放置了一个AB,剩下的AB数量是n1 - i - k个,我们需要把它分配到cnt个位置,这是个经典的组合数问题,方案数是C(n1 - i - k + cnt- 1, cnt - 1),所以:
复杂度O(n2);
Source:
/*created by scarlyw
*/
#include <cstdio>
#include <string>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>
#include <cctype>
#include <vector>
#include <set>
#include <queue>inline char read() {static const int IN_LEN = 1024 * 1024;static char buf[IN_LEN], *s, *t;if (s == t) {t = (s = buf) + fread(buf, 1, IN_LEN, stdin);if (s == t) return -1;}return *s++;
}///*
template<class T>
inline void R(T &x) {static char c;static bool iosig;for (c = read(), iosig = false; !isdigit(c); c = read()) {if (c == -1) return ;if (c == '-') iosig = true; }for (x = 0; isdigit(c); c = read()) x = ((x << 2) + x << 1) + (c ^ '0');if (iosig) x = -x;
}
//*/const int OUT_LEN = 1024 * 1024;
char obuf[OUT_LEN], *oh = obuf;
inline void write_char(char c) {if (oh == obuf + OUT_LEN) fwrite(obuf, 1, OUT_LEN, stdout), oh = obuf;*oh++ = c;
}template<class T>
inline void W(T x) {static int buf[30], cnt;if (x == 0) write_char('0');else {if (x < 0) write_char('-'), x = -x;for (cnt = 0; x; x /= 10) buf[++cnt] = x % 10 + 48;while (cnt) write_char(buf[cnt--]);}
}inline void flush() {fwrite(obuf, 1, oh - obuf, stdout);
}/*
template<class T>
inline void R(T &x) {static char c;static bool iosig;for (c = getchar(), iosig = false; !isdigit(c); c = getchar())if (c == '-') iosig = true; for (x = 0; isdigit(c); c = getchar()) x = ((x << 2) + x << 1) + (c ^ '0');if (iosig) x = -x;
}
//*/const int MAXN = 2000 + 10;
const int mod = 1000000000 + 7;int n1, n2, n3, n4;
int c[MAXN][MAXN], p[MAXN], f[MAXN], g[MAXN];inline int calc(int x, int y, int cnt) {if (cnt == 0) return (x + y == 0);if (x < y) std::swap(x, y);long long ans = 0;for (int i = x - y, end = std::min(x, cnt); i <= end; ++i) {int j = i - x + y, k = cnt - i - j;if (k < 0) break ;ans = (ans + (long long)c[cnt][i] * c[cnt - i][j] % mod * p[k] % mod * c[x - i - k + cnt - 1][cnt - 1]) % mod; }return ans;
}inline void solve() {R(n1), R(n2), R(n3), R(n4), p[0] = 1;if (n1 + n2 + n3 + n4 == 0) std::cout << "1", exit(0);for (int i = 0; i < MAXN; ++i) c[i][0] = c[i][i] = 1;for (int i = 1; i < MAXN; ++i) p[i] = (p[i - 1] << 1) % mod;for (int i = 2; i < MAXN; ++i)for (int j = 1; j < i; ++j)c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;for (int i = 0; i <= n1 + n2; ++i) f[i + 1] = calc(n1, n2, i);for (int i = 0; i <= n3 + n4; ++i) g[i + 1] = calc(n3, n4, i);long long ans = 0;for (int i = 1; i <= n1 + n2 + 1; ++i) ans += (long long)f[i] * (2LL * g[i] + g[i - 1] + g[i + 1]) % mod;std::cout << ans % mod;
}int main() {solve();return 0;
}