Codeforces Round 597 (Div. 2)___F Daniel and Spring Cleaning —— 数位DP

题目链接：点我啊╭(╯^╰)╮

题目大意：

    给出 $l，r$
    问满足以下条件的 $(a,b)$ 有多少对
    

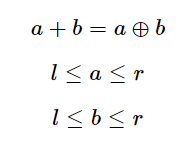
解题思路：

    $a+b=a?b$     $=>$     $a$ $\&$ $b=0$
    证明：$a?b$为没有进位的二进制加法，$a+b$ 为有进位的
    则若满足 $a+b=a?b$，则一定满足 $a$ $\&$ $b=0$

    然后开始数位$DP$，讨论 $a$ 与 $b$ 在 $(0,r)$ 的方案数
    满足 $a$ $\&$ $b=0$ 只需要在每一位的与为 $0$
    最后容斥以下即可

    题解的方法太过可怕

核心：数位DP + 容斥

#include<bits/stdc++.h>
#define fi first 
#define se second 
using namespace std;
typedef long long ll;
using pii = pair <int,int>;
const int maxn = 2e5 + 5;
int T, a[40], b[40];
ll dp[40][2][2];ll dfs(int wz, int lim1, int lim2){if(wz == -1) return 1;ll &ret = dp[wz][lim1][lim2];if(ret != -1) return ret;int up1 = lim1 ? a[wz] : 1;int up2 = lim2 ? b[wz] : 1;ret = 0; for(int i=0; i<=up1; i++)for(int j=0; j<=up2; j++){if(i & j) continue;ret += dfs(wz-1, lim1&&(i==up1), lim2&&(j==up2));}return ret;
}ll cal(int l, int r){if(l<0 || r<0) return 0;memset(dp, -1, sizeof(dp));for(int i=30; ~i; i--){a[i] = l >> i & 1;b[i] = r >> i & 1;}return dfs(31, 1, 1);
}int main() {scanf("%d", &T);while(T--){int l, r;scanf("%d%d", &l, &r);printf("%lld\n", cal(r, r) - 2*cal(l-1, r) + cal(l-1, l-1));}
}