Floyd’s Tortoise and Hare 环检测算法_综合

参考：Floyd判圈算法理解
参考：Floyd判圈算法（龟兔赛跑算法, Floyd’s cycle detection）及其证明
参考：Floyd’s Tortoise and Hare & 环检测算法

简介

Floyd判圈算法(Floyd Cycle Detection Algorithm)，又称龟兔赛跑算法(Tortoise and Hare Algorithm)。该算法由美国科学家罗伯特·弗洛伊德发明，是一个可以在有限状态机、迭代函数或者链表上判断是否存在环，求出该环的起点与长度的算法。

检测一个链表是否有环（循环节），如果有，确定环的起点以及环的长度

复杂度

时间复杂度： $O (n + m)$
空间复杂度： $O (1)$
$n$ 为起点 $S$ 到环入口 $P$ 的距离， $m$ 为环的长度

结论

$①$ ：环检测
两个指针 $t$ 和 $h$ ， $t$ 移动速度为 $1$ ， $h$ 移动速度为 $2$ ，判断是否相遇

$②$ ：找出环的入口节点
两个指针相遇后，将 $t$ 重新放到链表头，然后两个指针速度都为 $1$ ，再次相遇后，所在位置即为入口节点

$③$ ：计算环长度
两个指针都放在入口节点后， $t$ 移动速度为 $1$ ， $h$ 移动速度为 $0$ ，再次相遇，即可计算出环长度

例题： H. Pseudo-Random Number Generator

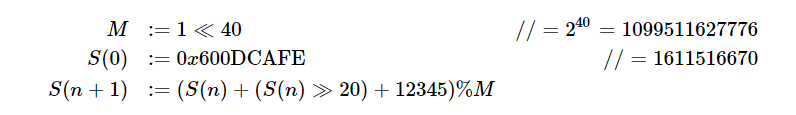
在这里插入图片描述

计算入口节点及环长度：

#include<bits/stdc++.h>
#define rint register int
#define deb(x) cerr<<#x<<" = "<<(x)<<'\n';
using namespace std;
typedef long long ll;
typedef pair <int,int> pii;
const ll mod = (1ll << 40);
inline ll nxt(ll x){return (x + (x >> 20) + 12345ll) % mod;
}signed main() {ll s0 = 0x600DCAFE, cnt = 0, num = 0;ll t = s0, h = s0;while(true){t = nxt(t), h = nxt(nxt(h));++cnt;if(!(t & 1)) ++num;if(t == h) break;}t = s0, cnt = num = 0;while(true){t = nxt(t), h = nxt(h);++cnt;if(!(t & 1)) ++num;if(t == h) break;}ll st_cyc = cnt, st_num = num;cnt = num = 0;while(true){t = nxt(t);
//		h = nxt(h);++cnt;if(!(t & 1)) ++num;if(t == h) break;}ll len_cyc = cnt, ans_cyc = num;deb(st_cyc); deb(st_num); puts("-----------");deb(len_cyc); deb(ans_cyc);
}

分块打表处理答案：

#include<bits/stdc++.h>
#define rint register int
#define deb(x) cerr<<#x<<" = "<<(x)<<'\n';
using namespace std;
typedef long long ll;
typedef pair <int,int> pii;
const ll mod = 1ll << 40;
const int base = 5e6;
inline ll nxt(ll x){return (x + (x >> 20) + 12345ll) % mod;
}ll mat[1010][2] = {1611516670, 1,6995323118, 2500401,14370630249, 5004364,24473902285, 7500029,38312556854, 10006017,57274551969, 12506329,83248007737, 15011683,118826730177, 17517443,167560289742, 20012408,234323188514, 22530434,325792323073, 25031296,451094609069, 27539195,622741727028, 30040232,857898708083, 32538480,937685173, 35042602,6072677726, 37541450,13107744445, 40042828,22744003927, 42546233,35943646365, 45056959,54027907086, 47548216,78802032994, 50056831,112739509636, 52565704,159235062884, 55056278,222913708970, 57559660,310147760736, 60057168,429642460847, 62554179,593348380684, 65062411,817588294774, 67574933,295498034, 70077204,5192879414, 72572034,11901289737, 75074286,21092425584, 77586589,33681877906, 80089334,50930014590, 82577797,74557367833, 85076566,106926639410, 87569837,151258698876, 90060817,211997026857, 92557144,295206930517, 95067617,409189858068, 97582000,565345893787, 100089173,779223572048, 102578453,1072246754882, 105080524,4354683110, 107578420,10752858133, 110081437,19518274761, 112579315,31526697331, 115071718,47977804257, 117584728,70512631458, 120091493,101383583168, 122603663,143677078963, 125100277,201601781662, 127598938,280954761586, 130104566,389678281232, 132606644,538598461112, 135114812,742592321221, 137604957,1022070324749, 140110603,3554026557, 142613775,9655697881, 145118771,18014204912, 147616701,29466792348, 150119937,45154383935, 152614526,66642984633, 155117508,96085200428, 157608613,136417233148, 160106698,191671943332, 162605678,267368060404, 165108248,371063286307, 167605345,513107125545, 170101751,707668644954, 172599641,974225187667, 175085228,2790547793, 177572982,8611289031, 180074324,16584933110, 182564868,27507640334, 185067560,42470755600, 187569610,62966213954, 190070901,91040988045, 192573754,129505250351, 195073010,182194153727, 197571938,254367017868, 200067363,353236621546, 202571441,488691710416, 205056578,674235835123, 207563824,928397275086, 210056612,2061291639, 212555608,7611195984, 215046440,15215211602, 217558986,25631359205, 220055532,39898870311, 222551803,59446145748, 225059431,86223613511, 227563092,122903535528, 230050444,173156136173, 232565955,241996682198, 235069888,336303276921, 237573994,465478252203, 240074925,642434794044, 242579118,884883721897, 245073898,1367467361, 247575267,6660774750, 250065868,13913445317, 252566347,23846914106, 255061631,37457188797, 257561860,56101519545, 260064780,81642081850, 262557086,116629560400, 265048248,164557000612, 267539163,230202910861, 270039390
};void pre() {ll x = 0x600DCAFE, ans = 1;printf("%lld,%lld,\n", x, 1);for (ll i=1; i<=542254520; ++i) {ll y = nxt(x);if (!(y & 1)) ans++;if (i % base == 0) printf("%lld,%lld,\n", y, ans);x = y;}
}int main() {ll st_cyc = 350125311;ll ans_cyc = 91029304;ll len_cyc = 182129209;ll n, ans;scanf("%lld", &n); n--;if (n <= st_cyc) {ans = mat[n / base][1];ll s = mat[n / base][0];for (ll i = n / base * base + 1; i<=n; ++i) {ll x = nxt(s);ans += !(x & 1);s = x;}if(n == -1) ans = 0;return printf("%lld\n", ans), 0;}ans = (n - st_cyc) / len_cyc;n -= ans * len_cyc;ans *= ans_cyc;ans += mat[n / base][1];ll s = mat[n / base][0];for (ll i = n / base * base + 1; i<=n; ++i) {ll x = nxt(s);ans += !(x & 1);s = x;}printf("%lld\n", ans);
}