[小样本医学图像分割]Data augmentation using learned transformations for one-shot medical image segmentation_综合

使用学习转换方法的数据扩充one-shot医学图像分割（CVPR2019）
论文地址
开源代码

摘要

本文提出了一种自动数据扩充方法来合成有标记的医学图像。我们展示了这一方法在分割大脑核磁共振成像（MRI）上的表现，我们的方法只需要一次分段扫描，并且在半监督的方法中利用了其它未标记的扫描。我们从图像中学习转换模型，并使用该模型和标记的示例来合成其他标记的示例。
每个变换都由空间变换和强度变换组成，能够合成复杂的效果，模拟解剖和图像采集程序的变化。

目前存在的问题和方案

在医学图像的采集过程中，不同机器和机构的图像采集程序的差异加剧了有限标记数据的问题，这可能会产生分辨率、图像噪声和组织外观的巨大差异。为了克服这些挑战，许多监督生物医学分割方法关注于手工预处理步骤和架构。通常也会使用手动调整的数据增强来增加训练示例的数量。数据增强函数，如随机图像旋转或随机非线性变形，很容易实现，并且在某些设置下可以有效地提高分割精度。然而，这些函数模拟真实变量的能力有限，并且对参数的选择非常敏感。

我们通过合成多样且真实的标记样本来解决有限标记数据的问题，这一新的数据扩充方法利用了未标记的图像。利用基于学习的配准方法，我们对数据集中图像之间的空间和外观变换进行了建模。这些模型捕捉了未标记图像的解剖学特性和成像多样性，我们通过采样这些转换来合成新的样本，并将它们应用到单个标记的例子中。

方法

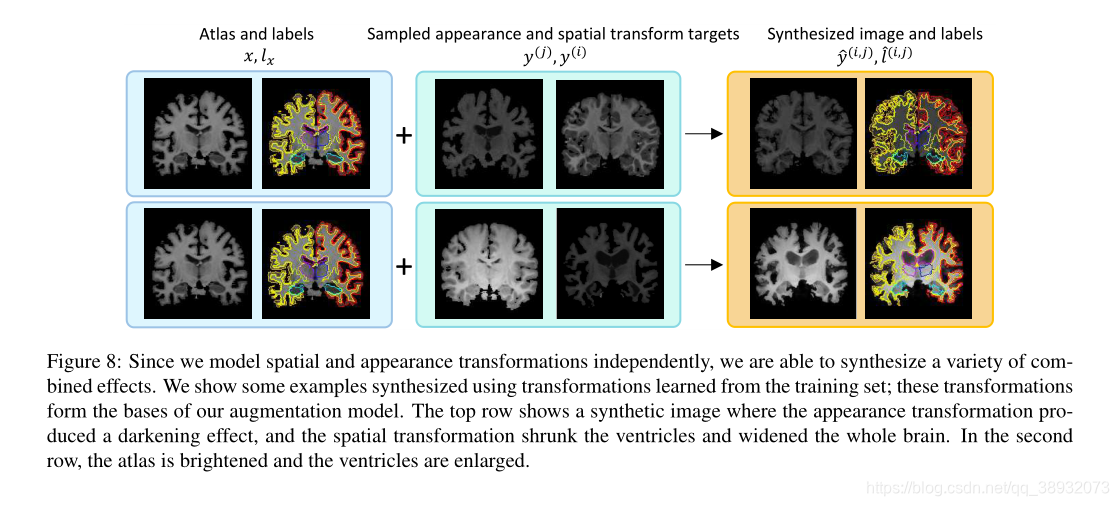
在这里插入图片描述

我们提出在半监督学习框架下综合真实的训练实例来改进one-shot生物医学图像分割的方法。

假定 ${y(i)}\left\{ y^{\left( i \right)} \right\}$ 是一组生物医学图像体，让图像对 $x,l_x)$ 表示一个标注的参考体，或者说atlas，以及其对应的分割图。在脑MRI分割中，每一个 $x$ 和 $y$ 都是一个灰度3D体。我们关注的是只有一个标记地图集是可用的情况，因为在实践中往往很难获得许多标注的分割体。我们的方法可以很容易地扩展到利用额外的分割体信息。

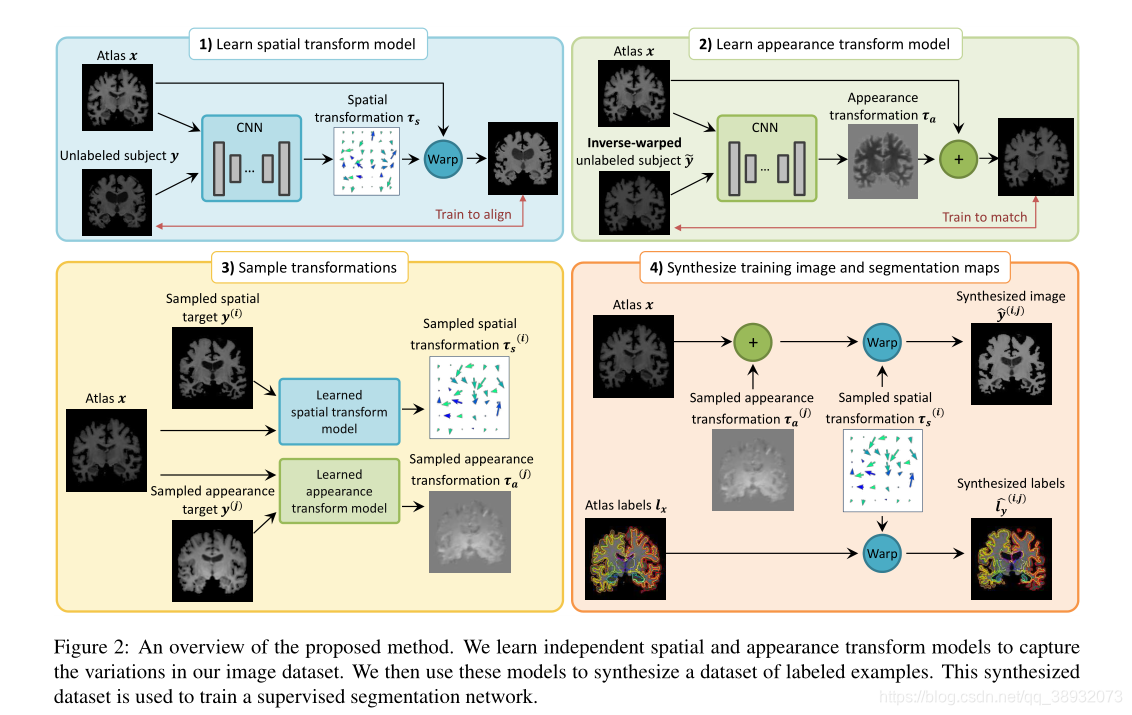
为了进行数据扩展，我们对标记的atlas $x$ 使用变换 $τ(k)\tau ^{\left( k \right)}$ 。我们首先学习空间转换（spatial transform）和外观转换（appearance transform）模型来捕捉标记的atlas和未标记的volume之间的解剖和外观差异。然后使用这两个模型，通过对atlas应用空间变换和外观变换来合成标记体 ${(y^(k),l^y(k))}\left\{\left(\hat{y}^{(k)}, \hat{l}_{y}^{(k)}\right)\right\}$ 。与单atlas分割存在空间变换模型不确定性或误差的情况相比，我们使用相同的空间变换来合成volume和label map，确保新合成的volume得到正确的标记。这些合成的例子形成了一个标记数据集，它描述了未标记数据集的解剖和外观变化。与atlas一起，这个新的训练集使我们能够训练有监督的分割网络。

Spatial and appearance transform models

我们使用空间和强度变化的组合来描述扫描之间的差异。具体来说，我们将 $τ(?)\tau \left( \cdot \right)$ 定义为空间变换 $τs(?)\tau _s\left( \cdot \right)$ 和强度(外观)变化 $τa(?)\tau _a\left( \cdot \right)$ 的组合，也即 $τ(?)=τs(τa(?))\tau(\cdot)=\tau_{s}\left(\tau_{a}(\cdot)\right)$ 。

我们假设空间变换采用平滑的体素级(voxel-wise)位移场 $u$ 的形式。根据医学文献，我们定义了变形函数 $?=id+u\phi=\mathrm{id}+u$ ，其中 $i d$ 是身份函数。我们使用 $\circ \phi$ 表示空间变换 $?\phi$ 对 $x$ 的应用。为了模拟数据集中空间变换的分布，我们使用 $?(i)=gθs(x,y(i))\phi^{(i)}=g_{\theta_{s}}\left(x, y^{(i)}\right)$ 将atlas $x$ 扭曲成每个volume $y^{(i)}$ 的变形，我们将 $y^{(i)}$ 到 $x$ 的逆变换写作 $??1(i)=gθs(y(i),x)\phi^{-1^{(i)}}=g_{\theta_{s}}\left(y^{(i)}, x\right)$ 。

我们对外观变换 $τa(?)\tau _a\left( \cdot \right)$ 建模为在atlas的空间框架中逐体素叠加。我们使用函数 $ψ(i)=hθa(x,y(i)???1(i))\psi^{(i)}=h_{\theta_{a}}\left(x, y^{(i)} \circ \phi^{-1^{(i)}}\right)$ 计算每个体素的volume，其中 $y(i)???1(i)y^{(i)} \circ \phi^{-1^{(i)}}$ 表示一个使用我们学习的空间模型转换到atlas空间的volume。综上所述，我们对空间和外观变换表示为:
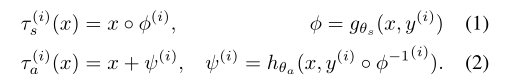
在这里插入图片描述

Learning

我们的目的是捕捉atlas与未标记体之间的转换分布 $τs(?)\tau _s\left( \cdot \right)$ 和 $τa(?)\tau _a\left( \cdot \right)$ 。我们使用单独的卷积神经网络来估计函数 $gθs(?,?)g_{\theta_{s}}(\cdot, \cdot)$ and $hθa(?,?)h_{\theta_{a}}(\cdot, \cdot)$ ，每个网络使用如图3所示的架构：
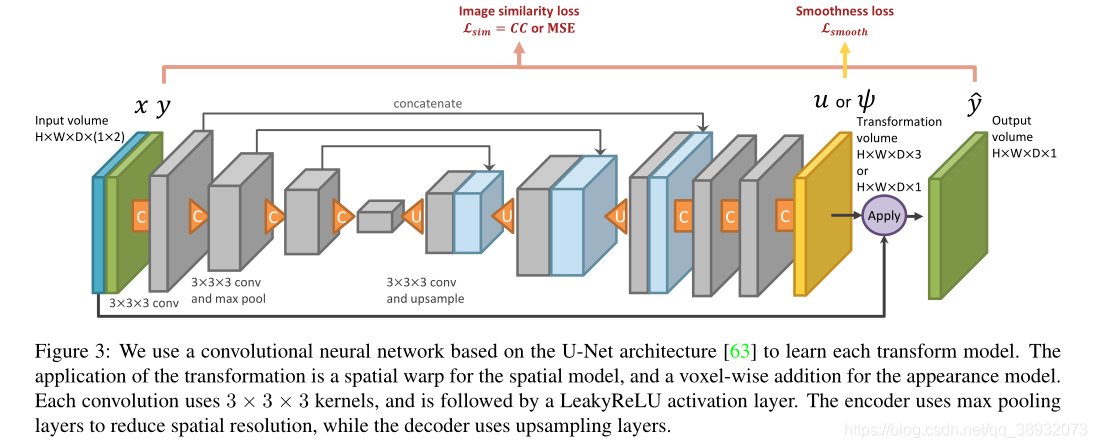
在这里插入图片描述
对于我们的空间模型，我们利用了VoxelMorph，这是一种最新的基于无监督学习的开源实现方法。VoxelMorph学习输出平滑的位移矢量场，通过联合优化图像相似损失和位移场平滑项来实现一张图像到另一张的转化。我们使用一种具有归一化互相关的VoxelMorph变体作为图像相似度损失，使未归一化输入量的 $gθs(?,?)g_{\theta_{s}}(\cdot, \cdot)$ 的估计成为可能。

我们使用类似的方法来学习外观模型。具体来说，可以将Eq.(2)中的 $hθa(?,?)h_{\theta_{a}}(\cdot, \cdot)$ 定义为atlas空间中volume的简单逐体素减法。这种变换可以完美地重建目标图像，当配准函数 $??1\phi^{-1}$ 不完善时，它将包括无关的细节，导致图像中的 $x+ψx+\psi$ 细节与解剖标签不匹配。因此，我们将 $hθa(?,?)h_{\theta_{a}}(\cdot, \cdot)$ 设计为一种神经网络，以解剖学对齐的方式产生每体素的强度变化。具体来说，我们使用了图像相似性损失以及语义感知平滑正则化。给定网络输出 $ψ(i)=hθa(x,y(i)???1)\psi^{(i)}=h_{\theta_{a}}\left(x, y^{(i)} \circ \phi^{-1}\right)$ ，我们根据atlas分割图定义一个平滑正则化函数：
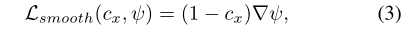
在这里插入图片描述
其中 $c_x$ 是由atlas分割标签 $l_x$ 计算出的解剖边界的二值图像， $▽\triangledown$ 表示空间梯度算子。直观地说，这个公式组织同一解剖区域内剧烈的强度变化。

在整体外观变换模型损失 $La\mathcal{L}_a$ 中，我们使用均方误差来计算图像相似度损失 $Lsim?(y^,y)=∥y^?y∥2\mathcal{L}_{\operatorname{sim}}(\hat{y}, y)=\|\hat{y}-y\|^{2}$ 。在我们的实验中，我们发现计算空间框架内的图像相似度损失是有帮助的。我们用正则化项 $Lsmooth\mathcal{L}_{smooth}$ 来平衡相似损失：
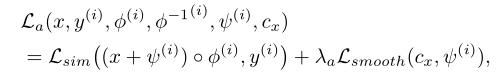
在这里插入图片描述

Synthesizing new examples

公式(1)和(2)所描述的模型使我们能够通过对未标记数据集中采样的目标volumes $y^{(i)}$ 和 $y^{(j)}$ 实现空间和外观变换 $τs(i),τa(j)\tau_{s}^{(i)}, \tau_{a}^{(j)}$ 。由于空间和外观目标可以是不同的主体，我们的方法可以将一个主体的空间变化与另一个主体的强度结合成一个单一的合成volume $y^\hat{y}$ 。我们通过应用从目标volume到带标签的atlas计算的转换来创建一个带标签的合成样本：
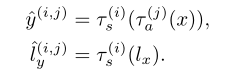
在这里插入图片描述

实验结果

在这里插入图片描述