1070 结绳 (25 分)
给定一段一段的绳子,你需要把它们串成一条绳。每次串连的时候,是把两段绳子对折,再如下图所示套接在一起。这样得到的绳子又被当成是另一段绳子,可以再次对折去跟另一段绳子串连。每次串连后,原来两段绳子的长度就会减半。
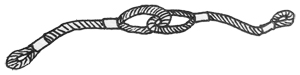
给定 N 段绳子的长度,你需要找出它们能串成的绳子的最大长度。
输入格式:
每个输入包含 1 个测试用例。每个测试用例第 1 行给出正整数 N (2≤N≤10?4??);第 2 行给出 N 个正整数,即原始绳段的长度,数字间以空格分隔。所有整数都不超过10?4??。
输出格式:
在一行中输出能够串成的绳子的最大长度。结果向下取整,即取为不超过最大长度的最近整数。
输入样例:
8
10 15 12 3 4 13 1 15
输出样例:
14
这是一道贪心的题目。
本题思想:由于题目中有最大两个字,而且按照题目把绳子对折的要求,可以得出:要是想得到的最后结果最大,则最长的那根绳子对折的次数最少(对折一次即为最少),同理,最短的那根绳子对折多次。那么就可以引出我们的贪心策略。
#include <iostream>
#include <algorithm>using namespace std;const int maxn = 2e4+10;int main()
{int n,i;cin>>n;double arr[maxn] = {0.0};for(i=0; i<n; i++){cin>>arr[i];}sort(arr,arr+n);for(i=1; i<n; i++){arr[i] = arr[i]/2 + arr[i-1]/2;}cout<<(int)arr[n-1]<<endl;return 0;
}