图像分类介绍和一些损失函数（hinge loss cross-entropy softmax得分介绍）

图像分类

图形分类介绍

对于输入的图像赋予一个标签，这个标签在指定的集合中。

例如：

图片也可以看成数组（大型三维数组）。

挑战：

1、单个物体从不同角度照的照片。
2、图像大小的问题（大头贴，全身照）
3、物体形状（水 冰）
4、遮挡问题
5、光照影响（白天 晚上）
6、物体和环境融合
7、同一个对象有不懂类别（椅子）

近邻分类器

• 数据驱动方式
  提供每个类别的很多样本，进行算法学习，去识别，也就是用更多的情况去学习。
  我们以CIFAR-10的例子进行介绍近邻分类器是如何进行分类。简单介绍一下该数据集，这个数据集由60000个32像素?和宽组成的?图像组成。每个图像都被标记为10个类之?（例如 ?机、汽?、?等），6W张图片，每个类别6K张，其中已经划分好了训练集5W个，测试集1W张图片。

这个算法需要比较距离，具体怎么进行距离之间的比较，有很多种方法，但是我们所使用的方法是L1距离，也就是图片中，每个像素点之间的差值绝对值，当做距离。

分类器及损失

基于图像像素映射的分类评分函数
SVM好人Softmax线性分类及其损失函数特点原理

线性分类

也就是我们的分类器是三条直线来区别类别：

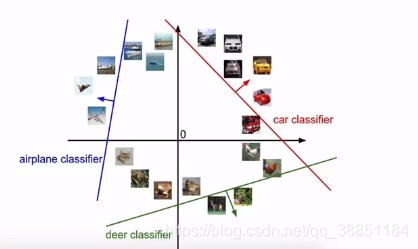
W每一行对应一个分类器。权重是怎么去得到的？
学习到的权重：解释，w的每一行对应于其中一个类的模板。然后，通过使用内部积逐个比较叫每个模板和图像来获得图像的而每个类的分数，以找到“最适合”的模板。
存在问题：每个类别只能学到一个模板，学习能力是有限的。无法进行非线性分类。

损失函数

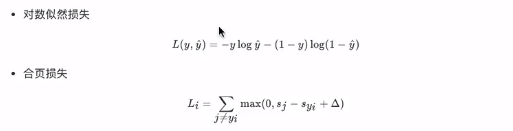
多分类的损失？hinge loss和交叉熵损失

hinge loss （合页损失）

其中，sj是预测概率，syi是预测正确的概率。举例说明：

以上三个图片分别为：猫、撤、青蛙，每张图片下面的数字分别表示预测为猫、车、青蛙的概率，由公式可以得出：猫的损失为

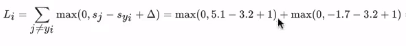
，车的损失为：

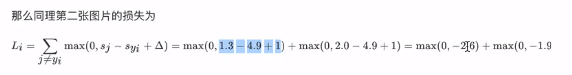
，青蛙损失为：

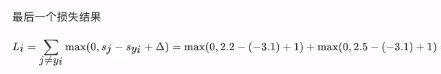
，最终三个有样本的平均合页损失为：

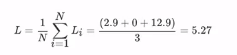
。由上图可以看出，当预测对了一个样本，并且改预测概率是最高的，那么这个样本的合页损失为0。上图的合页损失函数的概率得分可视化在下图中：

这张图的意思是：一个样本，蓝色是预测正确的概率（假设其预测正确），并且这个预测正确的类别的概率得分，比其它预测类别概率得分大于delta（本例子中delta的值为1），那么就不进行计算损失（因为max(0,<0)），其实就是在计算合页损失的时候增加了一个简化版的判断而已。也就是能够通过合页损失去测量这个误差。

Softmax分类与交叉熵损失

1、Softmax
之前学习softmax时，学的晕晕乎乎的。终于想明白了。其实神经网络的输出并不是一个个的在[0,1]之间的分数，而是一些得分，但是这些得分有些很大有些很小，就给损失函数造成了困难。那么研究人员想了一个办法，那就是将预测得分，映射到[0,1]之间，这样数据不仅仅都进行了规范化，而且也很方便了损失函数。我们能想到的最好的基本初等函数就是指数函数，因为指数函数的值永远大于零。
softmax是一种多分类器。对于一个更合适的输入即归一化的类别概率。
公式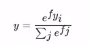：这个公式必须掌握！！！其中：1、fj是分数向量汇总第j个类别的分数2、该分数的指数形式 / 所有的指数形式的和 为sofrmax函数，结果缩小到0~1之间的一个值，并且所有值相加为1。

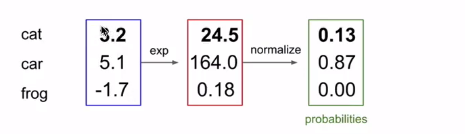
normalize即为归一化，即为softmax。
对于神经网络来说，损失函数为 cross-entropy。

cross-entropy

交叉熵损失是应用softmax分类之后如何计算损失大小的一种方式，这种方式来源于信息论。
公式：

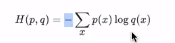
意义：

一句话总结：softmax相当于打分，cross-entropy相当于衡量预测和真实值之间的损失。

softmax数据稳定性问题

在交叉熵实际应用的时候，会出现一个问题，叫做：数据稳定性。也就是我们计算指数的时候，有些数进行指数运算后会非常的大，导致指数爆炸，产生数据溢出。解决办法：使用一个归一化方法。

C的值由我们自己定，通常取值为 logC= - maxj fj ，这样子分子就变成了1，也就是1/大数，让最大的概率映射之后接近于0。（学名：平移）。经过一些变换，这个公式也等价于：

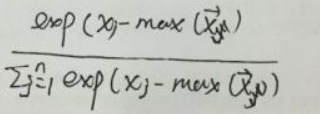
举例代码实现：

import numpy as np
f = np.array([123, 456, 789])
p = np.exp(f)/np.sum(np.exp(f))

报错："""Entry point for launching an IPython kernel.
数字产生了溢出，那么加上这个归一化的操作之后：

f -= np.max(f)
p = np.exp(f)/np.sum(np.exp(f))
print(p)
# array([5.75274406e-290, 2.39848787e-145, 1.00000000e+000])

softmax、cross-entropy和SVM hinge比较

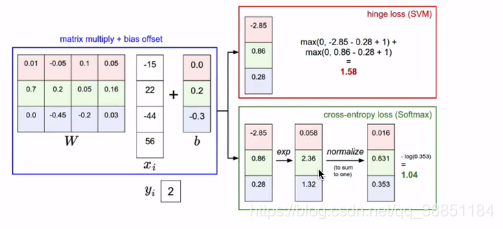
由上图可以看出二者的区别不是很大，实际应用中二者的表现是相当的，差异较小，但是我们总是倾向于选择更好的。那么二者的差异如下

• SVM下能够得到类别的判定，但实际上得到的类别得分，只是对这个类别的得分进行加减从而获得值，得分的绝对值大小并没有特别的含义。
• 
  SVM只关心分类边界。当我们选择的dartel为1的时候，{10，9, 9}和{10, 1，3}，这两个结果对于SVM来说，没什么却别，结果都是0。
• softmax分类器中，结果的绝对值大小表示属于该类别的概率。
  对于softmax而言，{10，9, 9}和{10, 1，3}是有差别的，softmax想让概率是正确的那个数值更大一些，是一个永远不会满足的分类器。