等式约束问题定义
1.1 有效集的定义

1.2 等式约束与拉格朗日等价

推导过程


1.3不等式与互补拉格朗日求解

推导


即 在内部目标函数梯度为0,在边界目标函数与约束梯度同向。因为有上述两种情况,因些需要第二个条件(互补条件)来对拉格朗日等式进行限定
1.3.2两个不等式约束


上述方法共性是 约束函数用泰勒一阶近似展开,因此当可行域中可行点附近不能有线性结构似无法成立


对于x 的二次方这样的函数,如果用一阶近似,则可行方向是可以任意取的,但只有0解,因 此需要假设确保可行域中c(x)可以用线性近似
1.4 线性化可行方向的定义

注意线性可行方向第一个对应等式约束,第二个代表不等式约束,在不等式约束中为什么没有考虑非积极的约束,如下对于非积极的话,如红色所示,cixc_ixci?x>0,的,可行方向d 相当于没有约束,可以任意取。只要第二项足够小
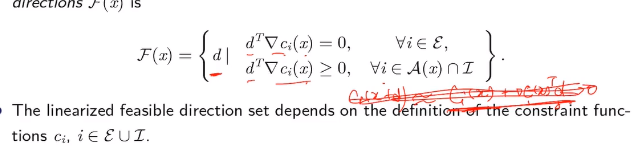
1.5 点的切锥



上面这个图中的点的切椎和可行的纯性化可行方向是相同的(有定理保证)(因为约束条件的梯度在最优点不为零,即不是线性相关的不存在非零向量线性组合为0 )

对于这个约束来说可行化方向是和切椎不同的(因为约束梯度为零的不满足线性无关),即切椎依赖于几何结构,而线性可行化方向是代数形式有关。
1.6 Constraint Qualifcations
当这个条件成立时,即线性可行方向和切椎相同,则=线性近似是可以反应最优点x 处的几何特征的(可以视为线性的),因此可以采用之前计论的线性近似

线性独立约束条件

2. 一阶必要性条件
如前,将不等或等式约束最优解求解转化为求解拉格朗日乘子的稳定点
2.1 KKT 条件

当成立时,只要找出最优点的积集,就将转换为了等式约束求解
注意KKT 是一阶心要性条件

上述证明中LICQ中满足,才可以利用线性近似,因此有d与目标函数在最优点的点积为非负,在LICQ成产时满足点积为正的可行方向称为序列可行方向(切椎方向),这个证明是在序列可行方向和线性可行方向相同时的结论,可参考最优化算法袁亚湘 定理8.2.7





zk 沿抛物线负半轴取向于原点,取tk 为趋向于0的到原点的距离,则d=(-l,0),l 为实数,若从(a,ka)直线趋近于0,则方向是过这点指向外侧,因此序列可行方向切椎为x轴上方的所有方向(0-pi)
