深度直接强化学习于金融信号表示和交易
发表于《IEEE TRANSACTIONS ON NEURAL NETWORKS AND LEARNING SYSTEMS 》期刊SCI一区
论文结构:
1、Introduction(综述论文,主要从决策执行RL和特征学习DL进行阐述)
2、Related works(介绍RL和DL相关知识)
3、Direct Deep Reinforcement Learning(正题部分,模型的构建顺序)
4、DRNN Learning(模型的初始化,训练方式)
5、Experimental Verifications(多种方法对比)
术语定义

TC trade commission 手续费
Abstract
Abstract—Can we train the computer to beat experienced traders for financial assert trading? In this paper, we try to address this challenge by introducing a recurrent deep neural network (NN) for real-time financial signal representation and trading. Our model is inspired by two biological-related learning concepts of deep learning (DL) and reinforcement learning (RL). In the framework, the DL part automatically senses the dynamic market condition for informative feature learning. Then, the RL module interacts with deep representations and makes trading decisions to accumulate the ultimate rewards in an unknown environment. The learning system is implemented in a complex NN that exhibits both the deep and recurrent structures. Hence, we propose a task-aware backpropagation through time method to cope with the gradient vanishing issue in deep training. The robustness of the neural system is verified on both the stock and the commodity future markets under broad testing conditions.
我们能训练电脑在金融交易中击败有经验的交易者吗?在本文中,我们试图通过引入一个递归的深度神经网络(NN)来解决这一挑战,用于实时金融信号的表示和交易。我们的模型是受两个生物相关学习概念的启发,即深度学习(DL)和强化学习(RL)。在该框架中,DL部分自动感知信息特征学习的动态市场条件。然后,RL模块与深度表示交互,做出交易决策,在未知的环境中积累最终的回报。该学习系统是在一个复杂的神经网络中实现的,该神经网络具有深度和递归结构。因此,我们提出了一种任务感知的时间反向传播方法来处理深度训练中的梯度消失问题。在广泛的测试条件下,神经系统对股票和商品期货市场的鲁棒性得到了验证。
Introduction
Deep Direct Reinforcement LeTraining intelligent agents for automated financial asserts trading is a time-honored topic that has been widely discussed in the modern artificial intelligence [1]. Essentially, the process of trading is well depicted as an online decision making problem involving two critical steps of market condition summarization and optimal action execution. Compared with conventional learning tasks, dynamic decision making is more challenging due to the lack of the supervised information from human experts. It, thus, requires the agent to explore an unknown environment all by itself and to simultaneously make correct decisions in an online manner. arning for Financial Signal Representation and Trading
Such self-learning pursuits have encouraged the long-term developments of RL—a biological inspired framework—with its theory deeply rooted in the neuroscientific field for behavior control [2]–[4]. From the theoretical point of view, stochastic optimal control problems were well formulated in a pioneering work [2]. In practical applications, the successes of RL have been extensively demonstrated in a number of tasks, including robots navigation [5], atari game playing [6], and helicopter control [7]. Under some tests, RL even outperforms human experts in conducting optimal control policies [6], [8]. Hence, it leads to an interesting question in the context of trading: can we train an RL model to beat experienced human traders on the financial markets? When compared with conventional RL tasks, algorithmic trading is much more difficult due to the following two challenges.
The first challenge stems from the difficulties in financial environment summarization and representation. The financial data contain a large amount of noise, jump, and movement leading to the highly nonstationary time series. To mitigate data noise and uncertainty, handcraft financial features, e.g., moving average or stochastic technical indicators [9], are usually extracted to summarize the market conditions. The search for ideal indicators for technical analysis [10] has been extensively studied in quantitative finance. However, a widely known drawback of technical analysis is its poor generalization ability. For instance, the moving average feature is good enough to describe the trend but may suffer significant losses in the mean-reversion market [11]. Rather than exploiting predefined handcraft features, can we learn more robust feature representations directly from data?
The second challenge is due to the dynamic behavior of trading action execution. Placing trading orders is a systematic work that should take a number of practical factors into consideration. Frequently changing the trading positions (long or short) will contribute nothing to the profits but lead to great losses due to the transaction cost (TC) and slippage. Accordingly, in addition to the current market condition, the historic actions and the corresponding positions are, meanwhile, required to be explicitly modeled in the policy learning part.Without adding extra complexities, how can we incorporate such memory phenomena into the trading system?
In addressing the aforementioned two questions, in this paper, we introduce a novel RDNN structure for simultaneous environment sensing and recurrent decision making for online financial assert trading. The bulk of the RDNN is composed of two parts of DNN for feature learning and recurrent neural network (RNN) for RL. To further improve the robustness for market summarization, the fuzzy learning concepts are introduced to reduce the uncertainty of the input data. While the DL has shown great promises in many signal processing problems as image and speech recognitions, to the best of our knowledge, this is the first paper to implement DL in designing a real trading system for financial signal representation and self-taught reinforcement trading. The whole learning model leads to a highly complicated NN that involves both the deep and recurrent structures. To handle the recurrent structure, the BPTT method is exploited to unfold the RNN as a series of time-dependent stacks without feedback. When propagating the RL score back to all the layers, the gradient vanishing issue is inevitably involved in the training phase. This is because the unfolded NN exhibits extremely deep structures on both the feature learning and time expansion parts. Hence, we introduce a more reasonable training method called the task-aware BPTT to overcome this pitfall. In our approach, some virtual links from the objective function are directly connected with the deep layers during the backpropagation (BP) training. This strategy provides the deep part a chance to see what is going on in the final objective and, thus, improves the learning efficiency. The DDR trading system is tested on the real financial market for future contracts trading. In detail, we accumulate the historic prices of both the stock-index future (IF) and commodity futures. These real market data will be directly used for performance verifications. The deep RL system will be compared with other trading systems under diverse testing conditions. The comparisons show that the DDR system and its fuzzy extension are much robust to different market conditions and could make reliable profits on various future markets. The remaining parts of this paper are organized as follows. Section II generally reviews some related works about the RL and the DL. Section III introduces the detailed implementations of the RDNN trading model and its fuzzy extension. The proposed task-aware BPTT algorithm will be presented in Section IV for RDNN training. Section V is the experimental part where we will verify the performances of the DDR and compare it with other trading systems. Section VI concludes this paper and indicates some future directions.
金融资产自动交易智能代理的深度直接强化训练是现代人工智能[1]中广泛讨论的一个历史悠久的课题。从本质上讲,交易过程被很好地描述为一个在线决策问题,涉及到市场状况总结和最优行动执行两个关键步骤。与传统的学习任务相比,由于缺乏来自人类专家的监督信息,动态决策更具挑战性。因此,它要求代理独自探索一个未知的环境,同时以在线方式做出正确的决策。为金融信号表示和交易
这种自我学习的追求促进了rl的长期发展,这是一种受生物学启发的框架,其理论深深植根于行为控制的神经科学领域。从理论的角度看,随机最优控制问题在开创性的工作[2]中得到了很好的阐述。在实际应用中,RL的成功已经在许多任务中得到了广泛的证明,包括机器人导航[5]、atari游戏[6]和直升机控制[7]。在某些测试中,RL甚至在执行最优控制策略[6]、[8]方面优于人类专家。因此,在交易的背景下,它引出了一个有趣的问题:我们可以训练一个RL模型来击败金融市场上有经验的人类交易员吗?与传统的RL任务相比,由于以下两个挑战,算法交易更加困难。
第一个挑战来自于金融环境的总结和表述方面的困难。金融数据包含大量的噪音、跳跃和移动,导致高度非平稳的时间序列。为了减少数据的噪声和不确定性,通常提取手工金融特征,如移动平均或随机技术指标[9]来概括市场状况。为技术分析寻找理想的指标在定量金融学中得到了广泛的研究。然而,众所周知,技术分析的一个缺点是泛化能力差。例如,移动平均特征足以描述趋势,但在均值回归市场[11]中可能遭受重大损失。与其开发预定义的手工特性,不如直接从数据中学习更健壮的特性表示?
第二个挑战来自于交易行为执行的动态行为。下单是一项系统的工作,需要考虑很多实际因素。频繁改变交易头寸(多头或空头)不仅对利润毫无贡献,而且由于交易成本(TC)和滑移而造成巨大损失。因此,除了当前的市场状况外,政策学习部分还需要明确的对历史行动和相应的立场进行建模。在不增加额外复杂性的情况下,我们如何将这种记忆现象纳入交易系统?
针对上述两个问题,本文提出了一种新的RDNN结构,用于在线金融资产交易的同时环境感知和递归决策。
RDNN的大部分由两部分组成:用于特征学习的DNN和用于RL的递归神经网络(RNN)。
为了进一步提高市场总结的鲁棒性,引入模糊学习概念来减少输入数据的不确定性。
虽然DL在图像和语音识别等许多信号处理问题上显示出了巨大的潜力,但就我们所知,这是第一篇将DL应用于设计一个真实的金融信号表示和自学强化交易系统的论文。
整个学习模型是一个高度复杂的神经网络,包含深度结构和递归结构。
为了处理递归结构,利用BPTT方法将RNN展开为一系列无反馈的时变栈。
当将RL分数传播回所有层时,训练阶段不可避免地涉及到梯度消失问题。
这是因为展开神经网络在特征学习和时间扩展两方面都表现出了极深的结构。
因此,我们引入了一种更合理的训练方法,称为任务感知BPTT来克服这一缺陷。
在我们的方法中,目标函数中的一些虚拟链接在反向传播(BP)训练中直接与深层连接。
这种策略为深入了解最终目标提供了一个机会,从而提高了学习效率。
DDR交易系统是在真实金融市场上对QIHUO合约交易的测试。
详细地,我们累积股票指数期货(IF)和商品期货的历史价格。
这些真实的市场数据将直接用于业绩验证。
在不同的测试条件下,深度RL系统将与其他交易系统进行比较。
结果表明,DDR系统及其模糊扩展对不同的市场条件具有较强的鲁棒性,并能在未来不同的市场上获得可靠的利润。
本文其余部分组织如下。
第二部分主要回顾了有关RL和DL的相关工作。
第三部分详细介绍了RDNN交易模型的具体实现及其模糊扩展。
提出的任务感知BPTT算法将在第四节中介绍,用于RDNN培训。
第五部分是实验部分,我们将验证DDR的性能并与其他交易系统进行比较。
第六部分对本文进行了总结,并提出了今后的研究方向。
II. RELATED WORKS
RL[12]是一种流行的自学[13]范式,它是为了解决马尔科夫决策问题[14]而开发的。根据不同的学习目标,典型的RL一般可以分为基于批评的(学习价值函数)和基于行为的(学习行为)两种类型。基于临界的算法直接估计可能是该领域中使用最多的RL框架的值函数。这些value-function-based方法。对于离散空间中的优化问题,通常采用TD-learning或Q-learning[15]来求解。数值函数的优化问题可以通过动态规划[16]来解决。
虽然基于价值函数的方法(也称为基于关键值的方法)在许多问题上表现良好,但如[17]和[18]所示,它不是一个很好的交易问题范例。这是因为交易环境过于复杂,无法用离散空间来近似。另一方面,在典型的q -学习中,价值函数的定义总是涉及到对未来贴现收益[17]进行重新编码的术语。交易的本质要求以在线方式计算利润。在交易系统的感觉部分或决策部分,不允许任何种类的未来市场信息。虽然基于值函数的方法对于离线调度器问题[15]是可行的,但是对于动态的在线交易[17]、[19]却不是很理想。因此,与学习价值函数不同,开创性的工作[17]建议直接学习属于基于参与者的框架的操作。
基于actor的RL直接从参数化的策略家族定义一系列连续操作。在典型的基于值函数的方法中,优化总是依赖于一些复杂的动态规划来获得每个状态的最优操作。基于行为的优化学习要简单得多,只需要一个带有潜参数的可微目标函数。此外,基于行为者的方法直接从连续的感官数据(市场特征)中学习策略,而不是用一些离散的状态来描述不同的市场情况(在Q-learning中)。综上所述,基于参与者的方法具有两个优点:1)优化目标灵活,2)对市场情况的描述连续。因此,它是一个比Q-learning方法更好的交易框架。在[17]和[19]中,基于参与者的学习被称为DRL,为了保持一致性,我们也将在这里使用DRL。
虽然DRL定义了一个良好的交易模型,但它并没有说明特性学习的方向。众所周知,鲁棒特征表示对机器学习性能至关重要。在股票数据学习的背景下,从[20]-[22]多个视角提出了各种特征表示策略。稳健特征提取的失败可能会对交易系统处理具有高不确定性的市场数据的性能产生不利影响。在直接增强交易(DRT)领域,Deng等人尝试引入稀疏编码模型作为金融分析的特征提取器。与DRL相比,稀疏特征实现了更可靠的性能。
虽然承认稀疏编码对于特征学习[23]-[25],[36]的一般有效性,但它本质上是一种浅层的数据表示策略,在广泛的测试[26],[27]中的性能无法与最先进的DL相比。DL是一种新兴的技术,它允许从大数据中学习健壮的特性。DL技术在图像分类[26]和语音识别[29]中取得了成功。在这些应用中,DL主要用于从大量的训练样本中自动发现信息特性。然而,据我们所知,目前几乎没有关于DL的金融信号挖掘的工作。本文将DL的能力推广到金融信号处理和学习的新领域。DL模型将与DRL相结合,为金融断言交易设计一个实时交易系统。
RL [12] is a prevalent self-taught learning [13] paradigm that has been developed to solve the Markov decision problem [14]. According to different learning objectives, typical RL can be generally categorized into two types as criticbased (learning value functions) and actor-based (learning actions) methods. Critic-based algorithms directly estimate the value functions that are perhaps the mostly used RL frameworks in the filed. These value-function-based methods,e.g., TD-learning or Q-learning [15] are always applied to solve the optimization problems defined in a discrete space. The optimizations of value functions can always be solved by dynamic programming [16].
While the value-function-based methods (also known as critic-based method) perform well for a number of problems, it is not a good paradigm for the trading problem, as indicated in [17] and [18]. This is because the trading environment is too complex to be approximated in a discrete space. On the other hand, in typical Q-learning, the definition of value function always involves a term recoding the future discounted returns [17]. The nature of trading requires to count the profits in an online manner. Not any kind of future market information is allowed in either the sensory part or policy making part of a trading system. While value-function-based methods are plausible for the offline scheduler problems [15], they are not ideal for dynamic online trading [17], [19]. Accordingly, rather than learning the value functions, a pioneering work [17] suggests learning the actions directly that falls into the actor-based framework.
The actor-based RL defines a spectrum of continuous actions directly from a parameterized family of policies. In typical value-function-based method, the optimization always relies on some complicated dynamic programming to derive optimal actions on each state. The optimization of actor-based learning is much simpler that only requires a differentiable objective function with latent parameters. In addition, rather than describing diverse market conditions with some discrete states (in Q-learning), the actor-based method learns the policy directly from the continuous sensory data (market features). In conclusion, the actor-based method exhibits two advantages: 1) flexible objective for optimization and 2) continuous descriptions of market condition. Therefore, it is a better framework for trading than the Q-learning approaches. In [17] and [19], the actor-based learning is termed DRL and we will also use DRL here for consistency.
While the DRL defines a good trading model, it does not shed light on the side of feature learning. It is known that robust feature representation is vital to machine learning performances. In the context of the stock data learning, various feature representation strategies have been proposed from multiple views [20]–[22]. Failure in the extraction of robust features may adversely affect the performances of a trading system on handling market data with high uncertainties. In the field of direct reinforcement trading (DRT), Deng et al. [19] attempt to introduce the sparse coding model as a feature extractor for financial analysis. The sparse features achieve much more reliable performances than the DRL to trade stock-IFs.
While admitting the general effectiveness of sparse coding for feature learning [23]–[25], [36], it is essentially a shallow data representation strategy whose performance is not comparable with the state-of-the-art DL in a wide range tests [26], [27]. DL is an emerging technique [28] that allows robust feature learning from big data. The successes of DL techniques have been witnessed in image categorization [26] and speech recognition [29]. In these applications, DL mainly serves to automatically discover informativefeatures from a large amount of training samples. However, to the best of our knowledge, there is hardly any existing work about DL for financial signal mining. This paper will try to generalize the power of DL into a new field for financial signal processing and learning. The DL model will be combined with DRL to design a real-time trading system for financial assert trading.
III. DIRECT DEEP REINFORCEMENT LEARNING
A. Direct Reinforcement Trading
内容主要有下面几点
- 穆迪的DRL框架[30],典型的DRL本质上是一个单层的RNN
- 提到了TC成本的问题
- 提到了TP可以直接作为Reward
- 然后可以用SHARP之类的去替换
B. Deep Recurrent Neural Network for DDR

- 对小穆的DRL换了网络结构单层变多层,隐藏层数设置为4,每个隐藏层的节点数固定为128。
C. Fuzzy Extensions to Reduce Uncertainties
- 使用了模糊神经网络的内容来处理原始数据
IV. DRNN LEARNING
虽然(8)中的优化在概念上很优雅,但不幸的是,它导致了相对困难的优化。这是因为所配置的复杂DNN包含数千个待推断的潜在参数。在本节中,我们提出了一个实用的学习策略,使用系统初始化和微调两个步骤来训练DNN。

A. System Initializations
参数初始化是训练神经网络的关键步骤。我们将介绍三个学习部分的初始化策略。
fuzzy representation 初始化比较简单,先用k-means将训练样本分成k个类。参数k固定为3
模糊表示部分[图3]。2(紫色面板)]容易初始化。唯一指定参数的模糊中心(mi)和宽度(σ2 i)的模糊节点,在那里我意味着我模糊的th节点成员层。我们直接使用k-means将训练样本分成k个类。参数k固定为3,因为每个输入节点都连接有三个隶属函数。然后在每个集群,每个维度的均值和方差的输入向量(英尺)是按顺序计算初始化相应的mi和σ2我。
采用AE初始化图2(蓝色面板)中的深度变换部分。简而言之,AE的目标是在隐藏表示之后的虚拟层上最优地重建输入信息。为了便于解释,这里指定了三个层,即,第(l)个输入层,第(l+1)个隐藏层,第(l+2)个重建层。这三层都连接得很好。我们定义hθ(·)[分别hγ(·)]的前馈转换从激光(l + 1) th层(分别(l + 1) th (l + 2) th层)和参数集θ(分别γ)。AE优化使以下损失最小化:
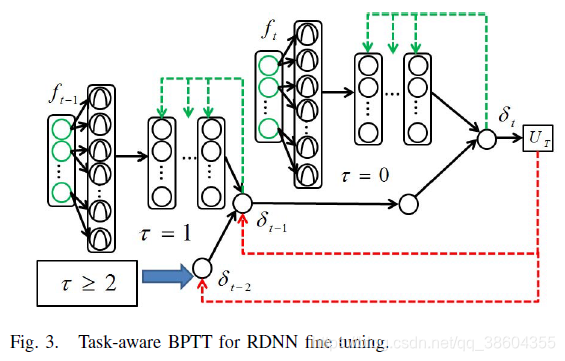
B. Task-Aware BPTT
- 这个是作者的contribution: Task-Aware BPTT
- 解决RNN梯度消失问题
- 目标函数中的一些虚拟链接在反向传播(BP)训练中直接与深层连接。
- 这种策略为深入了解最终目标提供了一个机会,从而提高了学习效率

V. EXPERIMENTAL VERIFICATIONS
A. Experimental Setup

我们在真实的财务数据上测试了DDR交易模型。股票指数和商品期货合约都将在本节中测试。对于股指期货数据,我们选择了我国首个基于指数的期货合约———股指期货合约。中证指数是根据沪深交易所前300只股票的价格计算出来的。IF期货是中国流动性最强、交易量最大的期货合约。在商品市场上,银(AG)和糖(SU)合约被使用,因为它们都表现出很高的流动性,使得交易行为几乎可以实时执行。所有这些合同都允许短期和长期操作。当随后的市场价格上涨(分别下跌)时,多头(分别做空)头寸获利。每个交易日的财务数据由我们自己的交易系统捕获,历史数据保存在数据库中。在我们的实验中,使用分钟级关闭价格,这意味着价格pt和pt+1之间有1分钟的间隔。三份合同在分钟决议中的历史数据如图4所示。
在这一年的时间里,IF合约积累的节拍比商品数据多,因为IF的每日交易周期比商品合约长得多。同样有趣的是,从图4中可以看出,这三种合约表现出了完全不同的市场模式。如果数据在测试期间有很大的上升和下降趋势。AG合同在测试期内一般呈下降趋势,SU没有明显的变化方向。在实际应用中,还应该考虑与交易相关的一些其他问题。我们在表一中总结了这些合同的一些详细信息。这三种合同的内在价值以每点人民币(CNY/pnt)计算。例如,在IF数据中,一个点的增加(减少)可能导致多头(分别是空头)获得300元的奖励,反之亦然。还提供了经纪公司收取的TCs。
通过考虑其他风险因素,在(1)中设置了一个高得多的c,是实际TCs的5倍。交易系统的输入直接使用最近45分钟的原价格变化和前3h、5h、1天、3天、10天的动量变化(ft∈R50)。
在模糊学习部分,将50个输入节点分别连接到3个模糊隶属函数中,寻找R150中的一级模糊表示。然后,模糊层依次通过四个深度转换层,每层有128、128、128和20个隐藏节点。
最后一层的特征表示(Ft∈R20)与DRL部分连接,用于交易决策。
B. Details on Deep Training
- BPTT和task-aware BPTT的收敛速度比较

C. General Evaluations
- DRL :DRL system [17].
- SCOT: sparse coding-inspired optimal training system [19]
- DDR :本文
- FDDR :本文
- P&L :profit and loss (P&L) curves


在本节中,我们将根据实际数据对DDR交易系统进行评估。该系统与其他在线交易RL系统进行了比较。第一个竞争对手是DRL系统[17]。此外,在本节中,我们利用稀疏编码启发的最优训练(SCOT),以实际数据对DDR交易系统进行了评价。该系统与其他在线交易RL系统进行了比较。第一个竞争对手是DRL系统[17]。利用稀疏编码的浅层特征学习部分,对基于稀疏编码的优化训练(SCOT)系统[19]进行了评价。最后,报告了DDR和FDDR的结果。在前面的讨论中,为RL定义的奖励函数被认为是训练期间获得的TPs。与总收益相比,在现代投资组合理论中,风险调整利润更广泛地用于评价交易系统的绩效。在这篇论文中,我们还将考虑一个替代的奖励函数到RL部分,即。,其中广泛应用于许多交易相关的著作[42],[43]。
SR被定义为在第一时期计算的回报率的平均回报率与标准差的比率,…, T,即。, USR T = (mean(Rt)/std(Rt))。为了简化表达式,我们使用DRL[17]中的相同思想来使用移动SR。一般情况下,移动SR得到典型SR的一阶泰勒展开,然后以增量的方式更新值。详细推导请参考[17,第2.4节]。以TP和SR为RL目标,对不同的交易系统进行培训。损益曲线如图6所示。定量评估总结在表二,其中测试性能也报告了TP和sr的形式。
购买和持有(B&H)的性能也报告在表二作为比较基线。从实验结果中可以得出以下三个观察结果。首先观察到的是,所有的方法都在趋势市场中获得了更多的利润。由于我们允许短线操作,交易者也可以在下跌的市场中赚钱。从IF数据可以看出,中国股市先是呈现上升趋势,然后突然下跌。FDDR在这两种情况下都能获利。同时还发现损益曲线在由上升趋势向下降趋势过渡期间存在一个缺陷。这可能是由于培训和测试数据的显著差异造成的。
一般来说,RL模型特别适用于趋势市场情况。其次,FDDR和DDR在所有市场上的表现一般都优于其他两家竞争对手。在大多数情况下,SCOT的性能也优于DRL。这一观察结果证实了特征学习确实有助于提高交易绩效。此外,与浅层学习方法(SCOT)相比,DL方法(FDDR和DDR)在所有测试中SR都更高,从而获得更多的利润。
在两种DL方法中,为模糊表示添加额外的层似乎是进一步改进结果的好方法。从表II和图6中可以很容易地验证这一说法,图6(g)中,除了图6(g)中的测试外,FDDR在所有测试中都获得了DDR。如前一段所述,DRL是一种趋势跟踪系统,在市场上可能遭受损失,波动较小。然而,从结果中可以看出,即使在非趋势期,如SU数据或IF数据的前期,FDDR也可以有效地使波动市场模式的正积累。这一发现成功地验证了模糊学习在减少市场不确定性方面的另一个重要性质。
第三,将SR作为RL目标,总是可以得到更可靠的性能。从表二的SR数量和图6的P&L曲线形状可以看出这种可靠性。从表二可以看出,在DDR中,通过优化TP作为目标,IF数据的利润最高。但是,该测试条件下的SR比其他条件下的SR差。在投资组合管理中,在可接受的风险水平内获得良好的利润,比在高风险下争取最高利润更为明智。因此,在实际应用中,仍然建议使用SR作为RL的奖励函数。综上所述,RL框架可能是一种基于趋势的交易策略,可以在价格波动较大的市场上获得可靠的利润(无论朝哪个方向)。基于dl的交易系统通常比其他DRL模型表现更好,不管有没有浅层特征学习。通过将模糊学习的概念引入系统,甚至可以在非趋势期产生良好的结果。在进行深度交易模型的训练时,建议使用SR作为RL目标,以较好地平衡利润和风险。
D. Comparisons With Prediction-Based DNNs
我们进一步将DDR框架与其他基于谓词的NNs[1]进行比较。这个基于预测的NN的目标是预测下一根(分钟分辨率)的闭合价格是会变高、变低,还是不变。卷积神经网络(convolutional DNN, CDNN)[26]、RNN[1]和long short-term memory (LSTM) [44] RNNs是主要的竞争对手。为了进行公平的比较,FDDR中的培训和测试策略同样适用于他们。我们寻求基于python的DL包Keras3来实现这三种比较方法。Keras为公共用途提供了卷积、递归和LSTM层的基准实现。CDNN由五层组成:1)输入层(50维输入);2)卷积层64个卷积核(每个卷积核长度为12);3)最大池化层;4)全连通致密层;5)软max层,3个输出。RNN包含一个输入层、一个密集层(128个隐藏的神经元)、一个重复层和一个用于分类的软最大层。LSTM-RNN除了使用LSTM模块替换循环层外,与RNN共享相同的配置。在实际应用中,对于基于预测的学习系统,只有可信度高的交易信号才是可信的。当单方向预测概率(软最大值函数的输出)大于0.6时,即为此类信号。我们已经报告了利润率(PR),交易时间(TTs),以及表三中不同交易成本的TPs。PR是通过盈利交易的数量除以总交易数量(TT)来计算的。研究结果是在中频市场上得到的。从表中可以看出,所有学习系统的PRs仅略高于50%。如此低的PR意味着在高度动态和复杂的金融市场中准确预测价格走势的难度。然而,低PR并不意味着没有交易机会。例如,考虑这样一个场景,赢的交易可以得到2分,输的交易平均损失1分。在这样的市场中,即使是40%的PR也能带来正的净利润。从我们的实验中可以观察到,在交易成本为零的情况下,所有的方法从IF数据中积累了相当可靠的利润。在此条件下,RDNN和LSTM算法的预测精度明显高于其他算法。然而,当考虑到实际的交易成本时,基于预测的DNN的缺陷就显而易见了。通过检查表III中的总TTs (TT列),预测系统可能比我们的FDDR更频繁地改变交易头寸。当交易成本增加到2个点时,只有FDDR能够实现正收益,而其他系统由于TCs沉重而损失惨重。这是因为基于预测的系统只考虑市场条件来进行决策。在FDDR中,我们考虑了当前的市场状况和交易行为,以避免沉重的交易成本。这是在一个联合的框架中学习市场状况和交易决策的好处。从数据中可以看出,训练数据和测试数据可能不具有相同的模式。金融信号不像其他固定或结构化的连续信号,如音乐,表现出周期性和重复的模式。因此,在本例中,我们放弃了递归记忆历史特征信息的传统RNN配置。相反,拟议的FDDR只考虑当前的市场状况和过去的交易历史。记住交易行为有助于系统保持一个相对较低的换位频率,以避免大量的TCs[17]。
E. Verifications on the Global Market
FDDR的表现也在全球市场上得到验证,交易标准普尔500指数。标普1990年1月至2015年9月的日分辨率历史数据来自雅虎财经,共计6500多天。在这个市场中,我们直接使用了前20天的价格变化作为原始特征。最近的2000个交易日(大约8年)用于训练FDDR,每100个交易日更新一次参数。在这种情况下,我们将交易成本固定为指数价值的0.1%。不同RL方法对1997年11月至2015年9月标普日数据的表现如图7所示。从结果可以看出,拟议的FDDR也适用于标准普尔指数。与绿色曲线(DRL)相比,紫色曲线(FDDR)的利润更高。DL框架比浅层DRL多出大约1000个点。值得注意的是,美国股市深受全球经济的影响。因此,我们也考虑了另一种生成FDDR学习特性的方法。其他主要国家的指数变化也提供给了FDDR。相关指数包括FTSE100指数(英国)、恒生指数(香港)、日经225指数(日本)和上证指数(中国)。由于不同国家的交易日可能不完全相同,所以我们采用S&P的交易日作为参考来对数据进行对齐。在其他市场,丢失的交易日的价格变化为零。这5个市场最近20天的价格变化对FDDR来说是一个长输入向量(R100)。利用多市场特征(multi-FDDR)的FDDR损益表如图7中的红色曲线所示。有趣的是,在第2800点(2010年1月)之前,FDDR的表现通常优于多FDDR。然而,在那之后,多fddr表现得更好。这可能是因为更多的算法交易公司在2010年之后进入了市场。因此,原材料价格的变化可能不像以前那么有信息。在这种情况下,同时监控多个市场的决策可能是一个明智的选择。
F. Robustness Verifications
在本节中,我们验证了FDDR系统的鲁棒性。本文的主要贡献是将DL概念引入到用于特征学习的DRL框架中。值得对特征学习部分进行详细的讨论,并进一步研究它们对最终结果的影响。这里的神经网络结构的研究包括不同数量的BPTT栈(τ),不同的隐藏层(左),和不同的节点数量每层(N)。这部分将讨论实验的实际如果数据从2014年1月到2015年1月。深度层的数量从l = 3到l = 5,每层的节点数分别在N = 64、N = 128和N = 256三个层次上测试。我们也测试的顺序BPTT扩张与τ= 2和τ= 4。在每个测试级别,样本外性能和相应的训练复杂度都报告在表IV中。对于测试性能,我们只报告TPs,训练成本以分钟为单位进行评估。计算是在一个有16 g RAM的8核3.2 ghz计算平台上实现的。结果表明,当N变大时,计算复杂度增加。这是因为相邻层的节点是完全连接的。一旦在一个层中使用更多的节点,未知参数的数量就会大大增加。但是,将N从128增加到256对提高性能的帮助不大。另一种方法不是增加N,而是增加表IV水平方向的层数l。通过分析不同层数的结果,可以得出DNN的深度对特征学习部分至关重要。这意味着层的深度对提高最终性能有很大帮助。当深度从3增加到5时,TP也有了明显的改善。同时,随着层数的增加,计算量也随之增加。在所有的DNN结构中,使用5层,每层256个节点,可以获得最佳的性能。在所有测试中,相应的计算成本也是最重的。在分析不同时间扩张订单(τ),我们还没有找到强有力的证据声称高BPTT顺序对性能有好处。当使用τ= 4,TP与每一款利用τ= 2设置非常相似。但是,通过扩展BPTT顺序的长度,增加了计算的复杂性。这种现象可能是由于长期记忆不如短期记忆重要。因此,在这种情况下,优先使用低阶的BPTT。根据前面的比较,我们选择了τ= 2,N = 128和l = 3作为默认RDNN设置。虽然进一步增加层数可能会提高性能,但是训练的复杂性也会增加。虽然这里讨论的交易问题不是高频设置,但是训练效率仍然需要明确考虑。因此,我们建议一个相对简单的神经网络结构,以保证良好的性能。
VI. CONCLUSION
本文将当代DL引入到一个典型的DRL框架中,用于金融信号处理和在线交易。这个系统的贡献是双重的。
首先,它是一个没有技术指标的交易系统,极大地解放了人们从大量的候选者中选择特性。这种优势是由于DL的自动特征学习机制。
此外,考虑到财务信号的性质,我们将模糊学习扩展到DL模型中以减少原始时间序列的不确定性。股票指数和商品期货合约的结果都证明了该学习系统在同时进行市场条件总结和最优行动学习时的有效性。
据我们所知,这是首次尝试将DL用于实时金融交易。虽然DDR系统的能力已经在本文中得到了验证,但仍有一些有前途的方向。首先,本文提出的所有方法都只处理一份资产。在一些大型对冲基金中,交易系统总是被要求能够同时管理大量资产。将来,DL框架将被扩展,以从多个资产中提取特性,并学习项目组合管理策略。
其次,金融市场不是静止的,它可能会实时变化。从过去的培训数据中获得的知识可能不能充分反映后续测试期的信息。如何智能地选择合适的训练周期仍然是该领域的一个开放问题。