2020ICPC·小米 网络选拔赛第一场 D.Router Mesh（tarjan 割点）

题目链接：https://ac.nowcoder.com/acm/contest/7501/D

tarjan的割点算法可以参考博文：https://blog.csdn.net/csyifanZhang/article/details/105370924

分析

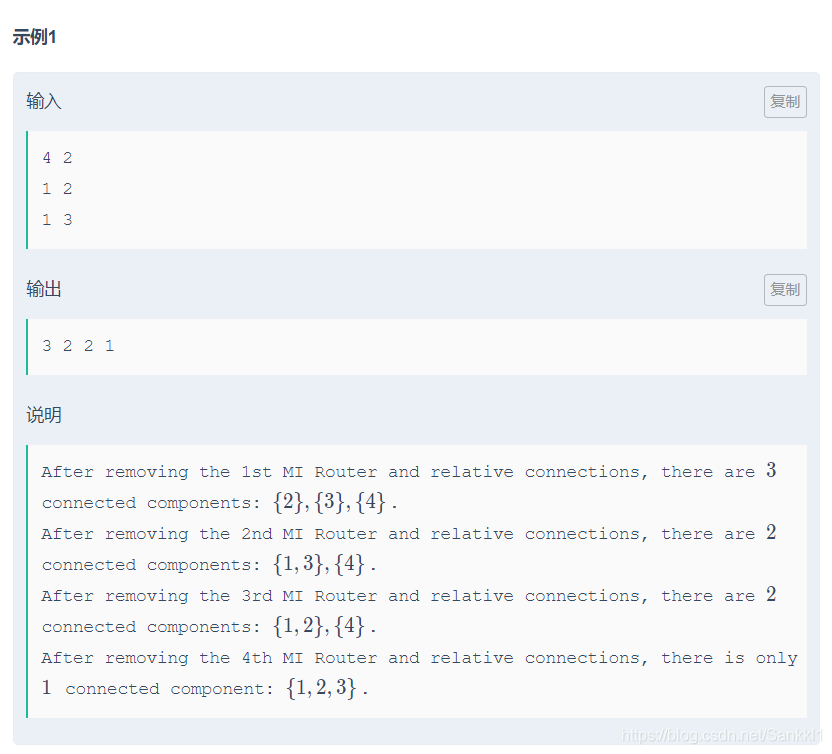
求一个图去掉第 i 个点后的连通块数量

分析

对于每个点，首先总共有 sum 个连通块，求出每个点所在的强连通分量的个数 x ，如果是割点，那么去掉以后还剩下 sum + x - 1 个连通块。
注意如果连通块只有一个点，那么去掉这个点后，连通块数会减少 1 。

代码

#include<bits/stdc++.h>
using namespace std;const int N = 300007;
int n,m;
int low[N],dfn[N],cut[N];
vector<int> g[N];
set<int> se;
int cnt;
int sum;void tarjan(int x, int root)
{
    low[x] = dfn[x] = ++cnt;int child = 0;for(int i=0;i<g[x].size();i++){
    int to = g[x][i];if(!dfn[to]){
    tarjan(to, root);low[x] = min(low[x], low[to]);if(low[to] >= dfn[x] && x != root) cut[x]++;if(x == root) child++;}low[x] = min(low[x], dfn[to]);}if(child >= 2 && x == root) cut[root] = child - 1;
}int main()
{
    scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){
    int u,v;scanf("%d%d",&u,&v);g[u].push_back(v);g[v].push_back(u);}for(int i=1;i<=n;i++){
    if(dfn[i] != 0) continue;sum++;tarjan(i, i);}for(int i=1;i<=n;i++)if(g[i].size() == 0)cut[i] = -1;for(int i=1;i<=n;i++){
    printf("%d ",sum + cut[i]);}return 0;
}