1. CTR概念
CTR, click through rate,指广告被点击次数 / 广告显示次数。
CTR预估模型公式: y = f ( x ) y = f(x) y=f(x), y ∈ [ 0 , 1 ] y \in [0, 1] y∈[0,1], 表示广告被点击的概率。
以下将介绍 LR, GBDT, FM, FFM, MLR, Deep and wide, Deep and Cross, deepFM, XDeepFM, PNN, NFM, AFM模型在CTR中的应用。
2. CTR 传统预估模型
2.1 LR
LR,logistic regression,是CTR预估模型的最基本模型,适用海量的高维离散特征。
f ( x ) = 1 1 + e ? θ T X f(x) = \frac{1}{ 1 + e^{-\theta^T X}} f(x)=1+e?θTX1?
其中, θ = ( θ 0 , θ 1 , . . . , θ n ) \theta = (\theta_0, \theta_1,..., \theta_n) θ=(θ0?,θ1?,...,θn?)
也可以表示为:
f ( x ) = l o g s t i c s ( l i n e a r ( X ) ) f(x)= logstics (linear (X)) f(x)=logstics(linear(X))
LR 的优势,处理离散化特征,模型简单,容易实现分布式计算。
LR变种,Google的FTRL, 可看做 LR + 正则化 + 特定优化方法。
FTRL算法的公式:
w t + 1 = arg ? min ? w ( ∑ s = 1 t g s ? w + 1 2 ∑ s = 1 t σ s ∥ w ? w s ∥ 2 2 + λ 1 ∥ w ∥ 1 ) \mathbf{w}_{t+1}=\underset{\mathbf{w}}{\arg \min }\left(\sum_{s=1}^{t} \mathbf{g}_{s} \cdot \mathbf{w}+\frac{1}{2} \sum_{s=1}^{t} \sigma_{s}\left\|\mathbf{w}-\mathbf{w}_{s}\right\|_{2}^{2}+\lambda_{1}\|\mathbf{w}\|_{1}\right) wt+1?=wargmin?(s=1∑t?gs??w+21?s=1∑t?σs?∥w?ws?∥22?+λ1?∥w∥1?)

LR缺点:
特征与特征之间在模型中是独立的,对于存在交叉可能性的特征,需要人工进行特征交叉。
2.2 GBDT
GBDT,梯度提升决策树,表达能力比较强的非线性模型。
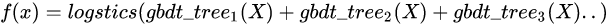
GBDT 的优势在于处理连续值特征,比如用户历史点击率。而且由于树的分裂算法,它具有一定的组合特征的能力。GBDT对特征的数值线性变化不敏感,它会按照目标函数,自动选择最优的分裂特征和相应的最优分裂点。并且,根据特征的分裂次数,得到一个特征的重要性排序。
缺点:
推荐系统的大多数场景都是大规模离散化特征,如果使用GBDT,则需要将很多特征统计成连续值特征(或者Embedding),这里需要耗费很多时间。GBDT模型具有很强的记忆行为,不利于挖掘长尾特征。
2.3 FM 和FFM
FM在LR不能自动处理交叉特征基础上改进。
FM模型:

逻辑斯蒂函数里边有两部分,一部分是,线性回归函数,第二部分是二次交叉项。
二次项权重 w i j w_{ij} wij? 需要存储一个二维矩阵的变量,这个二维矩阵的维度可能很大,FM利用矩阵分解的原理,将这个权重矩阵进行分解,即
 。
。
FM模型变成:


FFM模型公式:
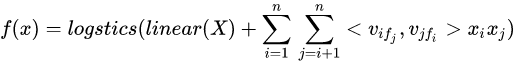
也就是, x i x_i xi? 和不同的特征交叉时,它的 v i v_i vi? 是不一样的。
FFM在FM的基础上,考虑了特征交叉的field的特点,但也导致了它没有办法实现线性的时间复杂度(假设n 个特征,一个特征 x i x_i xi?有 n ? 1 n-1 n?1 个 v i v_i vi? 个向量和其他特征的向量交叉,总共有 n ? ( n ? 1 ) 2 \frac{n*(n-1)}{2} 2n?(n?1)? 个向量的内积计算),模型训练比FM慢了一个量级,但效果比FM更好。
2.4 GBDT + LR/FM/FFM
GBDT 适合处理连续值特征,而 LR, FM, FFM更加适合处理离散化特征。GBDT可以进行一定程度的特征组合(多次组合),而FM,FFM只是二阶组合。同时,GBDT有一定的特征选择能力。也就是GBDT和LR,FM,FFM能够起到互补的作用。
Facebook 2014的论文 Practical Lessons from Predicting Clicks on Ads atFacebook 提出 GBDT + LR的解决方案,即先使用GBDT对一些稠密的特征进行特征选择,得到的叶子节点,再拼接离散化特征,放到LR 进行训练。
GBDT + LR模型:

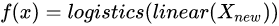
2.5 MLR
MLR 是由 阿里团队在 论文 Learning Piece-wise Linear Models from Large Scale Data for Ad Click Prediction 里提出的一种非线性模型,等价于 聚类 + LR的形式。
定义:
softmax ? ( X , i , m ) = e μ i X ∑ j = 1 m e μ j X \operatorname{softmax}(X, i, m)=\frac{e^{\mu_{i} X}}{\sum_{j=1}^{m} e^{\mu_{j} X}} softmax(X,i,m)=∑j=1m?eμj?Xeμi?X?
f ( x ) = ∑ i = 1 m softmax ? ( X , i , m ) ? logistics ? ( linear ? ( X ) ) f(x)=\sum_{i=1}^{m} \operatorname{softmax}(X, i, m) * \operatorname{logistics}(\operatorname{linear}(X)) f(x)=i=1∑m?softmax(X,i,m)?logistics(linear(X))
相当于将 X 进行聚成 m 类,然后,每一个聚类单独训练一个 LR。
MLR和LR一样,需要较大的特征工程处理,模型本身属于非凸模型(?),需要预训练,可能出现不收敛的情况。
3. CTR排序的DNN篇
CTR场景特征基本是离散化特征,而且特征之间交叉存在意义,使用DNN类的模型就有很强的模型表达能力,能够学习出高阶特征;同时容易扩充其他类别的特征,比如特征拥有图片、文字类特征时。
DNN模型的主要架构:

并行结构:

基本上目前的DNN模型和这个架构类似,只是stack layer的方法不一样,比如,有无 shallow part, 或者shallow part异同(如,用 LR 或FM等)。
串行结构:

下面是并行结构:
3.1 Deep and Wide model
Wide & Deep Learning for Recommender Systems;

shallow part 为 LR,stack layer为:concatenate(拼接Embedding后的向量)
Deep and Wide 网络 myblog;
3.2 Deep and cross model

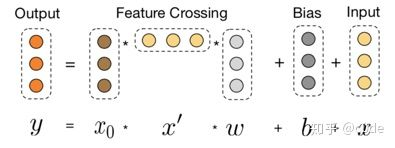
shallow part 为 cross Network,高阶组合,stack layer为:concatenate(拼接Embedding后的向量)
3.3 deepFM model

deepFM 的 shallow part 为 FM,stack layer 也是concatenate.
3.4 XDeepFM model


比较难理解的是(a)中两个矩阵外积得到一个三维数组,两个向量外积操作就能得到一个矩阵(一个截面),D 对就有D层截面。
(b)中把一个三维数组映射回二维数组,是对一个截面进行加权平均,得到一个向量。
(c)是整体图,每一层 x k x^k xk 都是由 x 0 x^0 x0 和前一层 x k ? 1 x^{k-1} xk?1 操作得到的。


xDeepFM 的 shallow part 为 CIN.
下面是串行结构:
3.5 PNN model
PNN,全称为Product-based Neural Network,认为在embedding输入到MLP之后学习的交叉特征表达并不充分,提出了一种product layer的思想,既基于乘法的运算来体现体征交叉的DNN网络结构。

l z l_z lz? 代表线性部分; l p l_p lp? 代表二次项部分特征.

定义:
p i , j = g ( f i , f j ) p_{i,j} = g(f_i, f_j ) pi,j?=g(fi?,fj?)
不同的g的选择使得我们有了两种PNN的计算方法,一种叫做Inner PNN,简称IPNN,一种叫做Outer PNN,简称OPNN。
IPNN
g ( f i , f j ) = < f i , f j > g(f_i, f_j ) = <f_i, f_j> g(fi?,fj?)=<fi?,fj?>
使用内积计算。

OPNN
外积计算。
定义:
g ( f i , f j ) = f i f j T g\left(f_{i}, f_{j}\right)=f_{i} f_{j}^{T} g(fi?,fj?)=fi?fjT?

3.6 NFM model
NFM model 的 deep part:

NFM的 shallow part 为 lr;stack layer 则为Bi-Interaction,实际上就是先做向量的内积,再做累加。
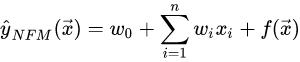
Bi-Interaction Layer名字挺高大上的,其实它就是计算FM中的二次项的过程,因此得到的向量维度就是我们的Embedding的维度。最终的结果是:

也就是:
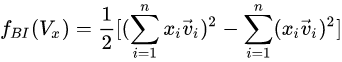
这里, x i v i x_i v_i xi?vi?是Embedding层的表示。每个Embedding特征叉乘并相加。
结果将是一个k维度向量, k就是embedding向量的长度.
3.7 AFM

注意,这里面省去了线性部分,只考虑特征组合部分。
Attention-based Pooling Layer:
Attention机制的核心思想在于:当把不同的部分压缩在一起的时候,让不同的部分的贡献程度不一样。AFM通过在Interacted vector后增加一个weighted sum来实现Attention机制。形式化如下:
f A t t ( f P I ( E ) ) = ∑ ( i , j ) ∈ R x a i j ( v i ⊙ v j ) x i x j f_{A t t}\left(f_{P I}(\mathcal{E})\right)=\sum_{(i, j) \in \mathcal{R}_{x}} a_{i j}\left(\mathbf{v}_{i} \odot \mathbf{v}_{j}\right) x_{i} x_{j} fAtt?(fPI?(E))=(i,j)∈Rx?∑?aij?(vi?⊙vj?)xi?xj?
Attention Network形式化如下:
a i j ′ = h T ReLU ? ( W ( v i ⊙ v j ) x i x j + b ) a i j = exp ? ( a i j ′ ) ∑ ( i , j ) ∈ R x exp ? ( a i j ′ ) \begin{aligned} a_{i j}^{\prime} &=\mathbf{h}^{T} \operatorname{ReLU}\left(\mathbf{W}\left(\mathbf{v}_{i} \odot \mathbf{v}_{j}\right) x_{i} x_{j}+\mathbf{b}\right) \\ a_{i j} &=\frac{\exp \left(a_{i j}^{\prime}\right)}{\sum_{(i, j) \in \mathcal{R}_{x}} \exp \left(a_{i j}^{\prime}\right)} \end{aligned} aij′?aij??=hTReLU(W(vi?⊙vj?)xi?xj?+b)=∑(i,j)∈Rx??exp(aij′?)exp(aij′?)??
就是乘了一个矩阵,在 Softmax 获得权重。
整体公式:
y ^ A F M ( x ) = w 0 + ∑ i = 1 n w i x i + p T ∑ i = 1 n ∑ j = i + 1 n a i j ( v i ⊙ v j ) x i x j \hat{y}_{A F M}(\mathbf{x})=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\mathbf{p}^{T} \sum_{i=1}^{n} \sum_{j=i+1}^{n} a_{i j}\left(\mathbf{v}_{i} \odot \mathbf{v}_{j}\right) x_{i} x_{j} y^?AFM?(x)=w0?+i=1∑n?wi?xi?+pTi=1∑n?j=i+1∑n?aij?(vi?⊙vj?)xi?xj?
4. 总结
DNN做CTR问题的关键有三:
- 是否保留浅层模型;
- 如何体现特征交叉性,即stack layer的做法。concatenate,Bi-interaction,直接向量相加等等。
- Embedding+ FC(全连接层)是标配。
最近开通了个公众号,主要分享推荐系统,风控等算法相关的内容,感兴趣的伙伴可以关注下。

参考:
- 推荐系统中使用ctr排序的f(x)的设计-dnn篇 - Jachin的文章 - 知乎;
- 推荐系统中使用ctr排序的f(x)的设计-传统模型篇 - Jachin的文章 - 知乎;
- 推荐系统遇上深度学习(六)–PNN模型理论和实践;
- 论文 Neural Factorization Machines for Sparse Predictive Analytics;
- Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks