第五章 代数系统基础
5.1 代数系统的一般概念
- 代数系统 是用代数运算方法构造系统的一门数学。所谓代数运算方法,即是在集合上建立满足一定规则的运算系统,并对该系统做定性的研究。
- 一个代数系统必须满足下面三个条件:
- 有一个非空集合S;
- 有一些建立在集合S上的一些运算。
- 这些运算在集合S上是封闭的。封闭的含义是说,运算得到的元素仍属于集合S。
5.2 代数系统常见的一些性质
- 以下即将提到的性质,并不是每个代数系统都有所有的这些性质。一个代数系统,可能只有部分以下性质。
- 单个二元运算的结合律:
(a x b) x c = a x (b x c)
- 单个二元运算的交换律:
a x b = b x a
- 单个二元运算的分配律:
a x (b # c) = (a x b) # (a x c)
- 单个二元运算的单位元素:
若代数系统 (S, #) 存在一个元素 1 ∈ S,均有 1 # x = x # 1 = x,则称1为S的对于运算‘#’的单位元素。这里1不是自然数1的意思,它是一个符号,表示单位元素的意思。
- 单个二元运算的零元素:
若代数系统 (S, #) 存在一个元素 0 ∈ S,均有 0 # x = x # 0 = 0,则称0为S的对于运算‘#’的零元素。这里0不是自然数0的意思,它是一个符号,表示零元素的意思。
- 单个二元运算的逆元素:
一个存在单位元素,且满足结合律的代数系统(S, x), 如果对S内的元素a,存在b ∈ S,使得 a x b = b x a = 1, 则b叫做a对运算 “x” 的逆元素,记作a^-1
5.3 同构和同态
同构:

- 同构的理解: 同构的本质,就是给集合中的每个元素都多了层包装。x1包装之后成了g(x1), x2 包装之后成了g(x2),以此类推。至于式5-1中,等式前是先运算之后再包装;等式右边是两个元素分别包装好之后,再做运算。
- 若两个代数系统同构,则这两个代数系统的特点相同,就是5.2节提到的那些性质。
同态:
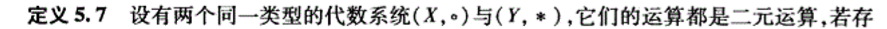

-
同态的理解: 同态的条件比同构松很多,同构要求那个包装函数g(x)是一个一一对应函数。相当于不同元素,经过g(x)的包装后,都不同。而同态,可以允许两个不同的元素经过g(x)包装之后得到同一个结果。
-
满同态:

- 同态的代数系统的性质关系:

5.4 常用的代数系统分类

第六章 群论
6.1 半群与单元半群
半群:

- 理解和记忆: 群,顾名思义一堆东西聚集在一起。因此,群 必须满足 最基础的一个性质:结合律。
- 循环半群:

一个定理:循环半群一定是可换半群。(即具有交换律的半群)
单元半群:

- 单元半群应该具有半群的那些性质和定理,因为单元半群也是一个半群。
6.2 群
群的基本性质:
- 群的定义:
群是一个具有结合律、单位元素、逆元素的代数系统。
- 可换群: 具有交换律的群叫做可换群。
- 群的阶: 若群中的元素个数是有限的,则群的阶就是群中元素的个数。若群中元素是无限的,则阶为无穷大。
- 群的性质:
- 群满足消去律。
- 一个阶大于1的群,一定没有零元素,因为零元素不存在逆元素。
- 除了单位元素之外,一个群一定没有幂等元素。
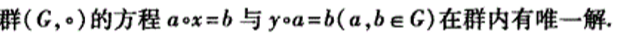
- 群的同构与同态:
群同构与群同态:

一个相关的定理: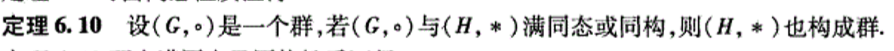
ps: 书上没有说明,同态则也是群,只说了满同态也是群。