线性方程组解的判定

解线性方程组就是求出解的集合。


- 曾广矩阵的秩大于系数矩阵的秩,无解
- 等于有解
- 不可能小于 ,曾广矩阵的秩一定大于等于系数矩阵的秩

齐次方程组解的判定定理
- n元齐次线性方程组有非零解的充要条件是系数矩阵的秩r(A)<nr(A)<nr(A)<n
- 只有零解 ,r(A)=nr(A)=nr(A)=n
线性方程组解的结构
齐次线性方程组


解的集合对向量运算是封闭的,解集是齐次线性方程组的解空间


- 基础解系不唯一,且不含零解
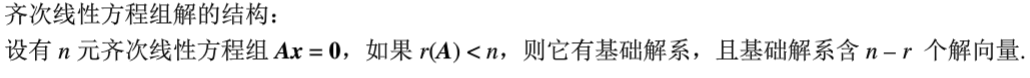
当秩小于n时,通解中存在n-r个任意参数
非齐次线性方程组


向量空间






基变换公式和坐标变化公式中 的系数矩阵互为逆矩阵。
reference
东北大学 线性代数mooc https://www.icourse163.org/course/NEU-1001638002?tid=1003308041