datawhale-异常检测打卡之Task 4：基于相似度方法

在异常检测中，我们弱化了“噪声”和“正常数据”之间的区别，专注于那些具有有价值特性的异常值。在基于相似度的方法中，主要思想是异常点的表示与正常点不同。

1 基于距离判断

基于距离的异常检测有这样一个前提假设，即异常点的k近邻距离要远大于正常点。计算当前点与其他点的距离，一旦已识别出多于k个数据点与当前点的距离在阈值D之内，则将该点自动标记为非异常值。

若是直接计算，需要计算每个点与其余点的距离，当数据量较大时，计算量非常大，因此需要利用基于单元、基于索引的方法加速计算。

1.1 基于单元格

在基于单元格的技术中，数据空间被划分为单元格。常用的一种是将每个维度被划分成宽度为$\frac{D}{d\sqrt{2}}$,D代表阈值，d代表数据维度，以二维情况为例，此时网格间的距离为$\frac{D}{2\sqrt{2}}$

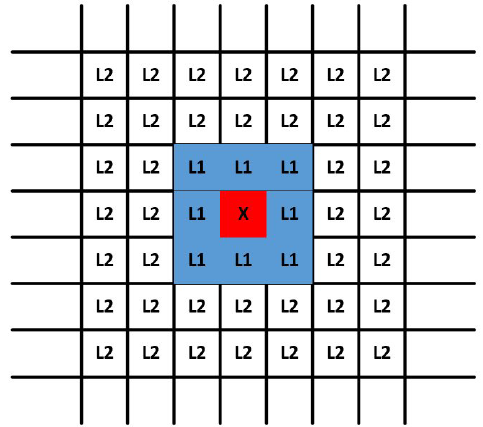
其$L_1$邻居被定义为通过最多1个单元间的边界可从该单元到达的单元格的集合。请注意，在一个角上接触的两个单元格也是$L_1$邻居。$L_2$邻居是通过跨越2个或3个边界而获得的那些单元格。如上图所示，X这个内部单元具有8个邻居和40个邻居。则可得出：

• 单元格中两点之间的距离最多为$\sqrt{2}?\frac{D}{2\sqrt{2}}=\frac{D}{2}$ 。
• 一个点与$L_1$邻接点之间的距离最大为$2\sqrt{2}?\frac{D}{2\sqrt{2}}=D$。
• 一个点与它的$L_r$邻居(其中$r$ > 2)中的一个点之间的距离至少为$D$。

唯一无法直接得出结论的是$L_2$中的单元格，这表示特定单元中数据点的不确定性区域。

step1 规则判断
如果一个单元格中包括其$L_1$超过k个数据点，那么这些数据点（单元格及$L_1$）都不是异常值
如果一个单元格中包括其$L_1，L_2$不超过k个数据点，那么这些单元格里的数据点都是异常值
step2 k最邻距离判断
对于此时仍未标记为异常值或者非异常值得单元格中的数据点需要明确计算其k最邻距离。

1.2 基于索引

基于索引的方法是利用多维索引结构来搜索每个数据点A在阈值D范围内的相邻点数，判断是否多于k个数据点与当前点的距离在阈值D之内。

2 基于密度判断

主要以局部离群因子(LocalOutlierFactor,LOF)算法为例讲解基于密度的算法

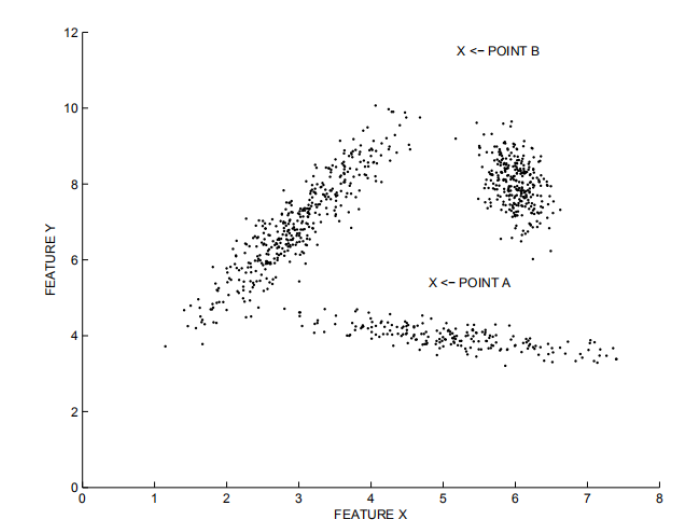
基于距离的检测适用于各个集群的密度较为均匀的情况，在下图中，离群点B容易被检出，而若要检测出较为接近集群的离群点A，则可能会将一些集群边缘的点当作离群点丢弃。而LOF等基于密度的算法则可以较好地适应密度不同的集群情况。

类似于在第一部分中距离的计算，我们也需要定义基于密度的度量值。

2.1 k-距离与可达距离

以对象o为中心，对数据集D中的所有点到o的距离进行排序，距离对象o第k近的点p与o之间的距离就是k-距离。

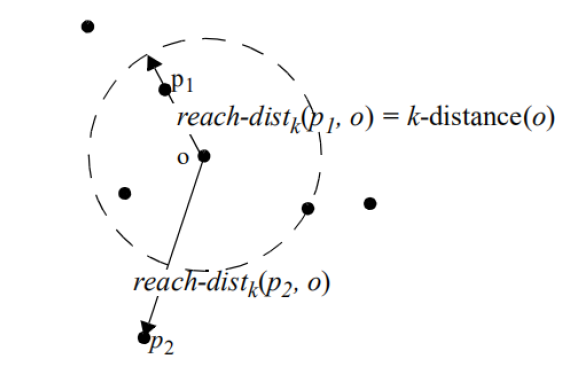
由k-距离，我们扩展到一个点的集合——到对象o的距离小于等于k-距离的所有点的集合，我们称之为k-邻域。k-邻域已经从“距离”这个概念延伸到“空间”了。

有了邻域的概念，我们可以按照到对象o的距离远近，将数据集D内的点$p_i$按照到o的可达距离分为两类：

• 若$p_i$在对象o的k-邻域内，则$p_i$可达距离就是给定点p关于对象o的k-距离；
• 若$p_i$在对象o的k-邻域外，则$p_i$可达距离就是给定点p关于对象o的实际距离。

2.2 局部可达密度与局部异常因子

可以将“密度”直观地理解为点的聚集程度，即点与点之间距离越短，则密度越大。使用数据集D中给定点p与对象o的k-邻域内所有点的可达距离平均值的倒数来定义$p_i$的局部可达密度。

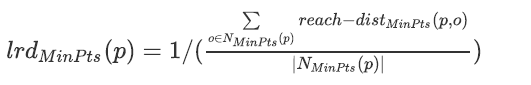
所以给定点p与对象o的k-邻域内点的可达距离越短，则其局部可达密度越高，则越可能与其邻域内的点 属于同一簇；密度越低，则越可能是离群点。

局部异常因子表示点p的邻域内其他点的局部可达密度与点p的局部可达密度之比的平均数。
如果这个比值越接近1，说明o的邻域点密度差不多，o可能和邻域同属一簇；如果这个比值小于1，说明o的密度高于其邻域点密度，o为密集点；如果这个比值大于1，说明o的密度小于其邻域点密度，o可能是异常点。

也即根据最终得出的LOF（局部异常因子）数值来进行是否异常点的判断。

3 总结

• 在基于相似度的方法中，主要思想是异常点的表示与正常点不同。
• 基于距离的异常检测有这样一个前提假设，即异常点的k近邻距离要远大于正常点，适用于各个集群的密度较为均匀的情况
• 基于密度的算法定义了一个LOF（局部异常因子）数值来进行是否异常点的判断，可以较好地适应密度不同的集群情况。

4 练习

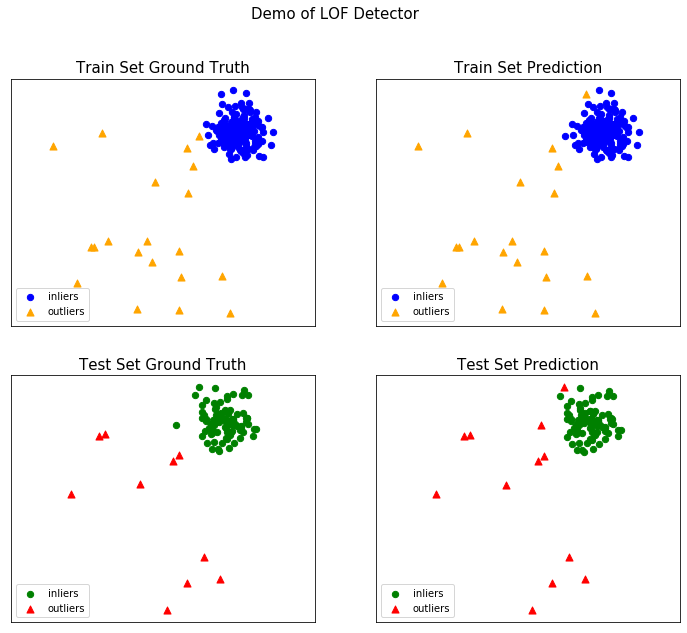
学习使用PyOD库生成toy example并调用LOF算法

from pyod.models.lof import LOF
from pyod.utils.data import generate_data
from pyod.utils.data import evaluate_print
from pyod.utils.example import visualizecontamination = 0.1  
n_train = 200 
n_test = 100  X_train, y_train, X_test, y_test = \generate_data(n_train=n_train,n_test=n_test,n_features=2,contamination=contamination,random_state=42)clf_name = 'LOF'
clf = LOF()
clf.fit(X_train)y_train_pred = clf.labels_  # binary labels (0: inliers, 1: outliers)
y_train_scores = clf.decision_scores_  # raw outlier scores
y_test_pred = clf.predict(X_test)  # outlier labels (0 or 1)
y_test_scores = clf.decision_function(X_test)  # outlier scores# evaluate and print the results
print("\nOn Training Data:")
evaluate_print(clf_name, y_train, y_train_scores)
print("\nOn Test Data:")
evaluate_print(clf_name, y_test, y_test_scores)visualize(clf_name, X_train, y_train, X_test, y_test, y_train_pred,y_test_pred, show_figure=True, save_figure=False)